1 aimantation induite

Soit une bobine parcourue par un courant continu d'intensité I (fig.1.a); cette bobine placée dans le vide crée un champ magnétique B_o = µ_o.k.I, µ_o = 4.p.10^-7 USI étant la perméabilité du vide.

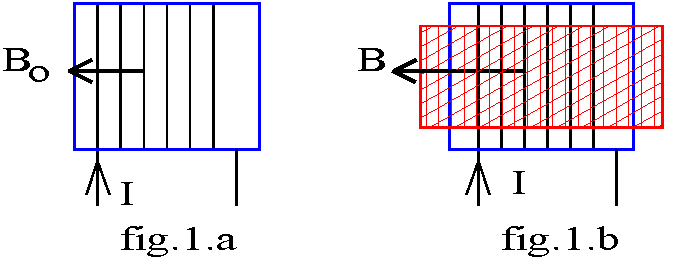
Plaçons un noyau de fer à l'intérieur de la bobine (fig.1.b); nous constatons une modification du champ. Les électrons des atomes du matériau, par leur rotation autour du noyau et autour d'eux-mêmes (spin), sont équivalents à des boucles de courant créant un champ magnétique donc une aimantation du matériau. Cette aimantation est quantifiée par un vecteur aimantation de module J fonction de l'excitation H = B_o/µ_o créée par la bobine.

La susceptibilité magnétique du matériau utilisé est définie par c = J / H. Cette aimantation se superpose à l'excitation de la bobine pour donner le champ résultant : B = µ_o.(J +H) soit B =µ_o.(1+c).H . Nous appelons perméabilité relative la quantité µ_r =1+c et perméabilité absolue la quantité µ = µ_o.µ_r

Dans un matériau magnétique magnétisé par un courant continu d'intensité I, nous définissons:

è l'excitation H exprimée en A/m et proportionnelle à I

è l'aimantation J = c.H exprimée en A/m

è le champ magnétique résultant : B = µ.H = µ_o.µ_r.H exprimé en tesla

.

2 Classification des matériaux

.

Les matériaux se classent suivant la valeur de la susceptibilité:

Ø Les matériaux diamagnétiques ont une susceptibilité c négative d'environ -10^-6 à -10^-5.

L'aimantation est due au mouvement des électrons autour du noyau. Le cuivre, le silicium, l'eau sont des matériaux de ce type.

Ø Les matériaux paramagnétiques ont une susceptibilité c positive d'environ 10^-8 à 10^-3.

L'aimantation est due à l'existence d'un moment magnétique pour chaque atome sans possibilité d'interaction entre les atomes. Sous l'effet de l'excitation H, les moments s'alignent suivant le champ magnétisant et créent une faible aimantation car l'agitation thermique perturbe fortement cet alignement. L'oxygène et l'aluminium sont des matériaux de ce type.

Pour ces deux types de matériau

èle champ est proportionnel à l'excitation, la perméabilité µ est constante. Ces matériaux sont dits linéaires.

èla faible valeur de la susceptibilité ne permet pas d'applications pratiques en électrotechnique.

Ø Les matériaux ferromagnétiques ont une susceptibilité élevée; les moments magnétiques des atomes sont fortement couplés entre eux; ce couplage permet leur orientation parallèlement au champ créant ainsi une forte aimantation. Le fer, le cobalt et le nickel sont les matériaux ferromagnétiques les plus courants.

.

Ø Les matériaux ferrimagnétiques ont une susceptibilité élevée; les moments magnétiques des atomes, fortement couplés entre eux, sont de deux types A et B; en l'absence d'excitation, les deux types de moments sont orientés en sens inverse; les moments de type B étant plus nombreux, il existe une aimantation permanente. En présence d'une excitation, l'orientation dans le même sens des deux types permet une forte aimantation. L'élévation de température diminue l'aimantation; au-delà de la température dite de Curie, le matériau perd ses propriétés magnétiques et devient de type paramagnétique. Les ferrites sont formés d'oxydes de fer et d'oxydes de divers matériaux tels que le zinc, le cobalt, le nickel...

Pour les matériaux ferromagnétiques et ferrimagnétiques :

èle champ n'est pas proportionnel à l'excitation, la perméabilité étant fonction de H; ces matériaux sont dits non linéaires.

èla forte aimantation de ces matériaux les rend indispensables dans les machines électriques.

 

3 Ferromagnétisme

3.1 Domaines magnétiques

Nous avons vu que le couplage fort des moments magnétiques dans ces matériaux tend à les orienter parallèlement. Cependant le matériau n'est pas aimanté en l'absence d'excitation. L'observation microscopique du matériau montre que, dans ce cas, l'orientation des moments n'est qu'un phénomène local. Le matériau est découpé en domaines dits de Weiss; à l'intérieur d'un domaine, tous les moments sont orientés parallèlement mais cette orientation change aléatoirement d'un domaine à l'autre donnant un moment résultant nul en l'absence d'excitation. Chaque domaine est séparé des voisins par une zone de transition où l'aimantation change progressivement de direction; cette zone est appelée paroi du domaine.

3.2 Caractéristique de première aimantation

Soumettons un échantillon de matériau ferromagnétique à une excitation croissante :

.

.

èAu départ (fig.2.a), H = 0 Représentons quatre domaines avec des orientations deux à deux opposées; l'aimantation est nulle ainsi que le champ B; le graphe B(H) dit courbe de première aimantation passe par l'origine O.

èCréons une excitation H (fig.2.b). Le domaine qui a l'orientation la plus voisine de H va s'étendre créant une aimantation dans le sens de l'excitation.

èTant que H est suffisamment faible, les parois des domaines restent accrochées entre elles en des points dits d'épinglage. Nous décrivons la partie OA₁ du graphe de façon réversible, c'est à dire que si nous ramenons H à 0 l'aimantation s'annule.

èLorsque l'excitation atteint une valeur critique, les points d'épinglage cèdent (fig.2.c) et le domaine aimanté dans la direction la plus voisine de H s'étend rapidement à tout l'échantillon; nous décrivons la partie A₁A₂ du graphe; le phénomène est alors devenu irréversible : en ramenant H à 0 nous n'annulons plus l'aimantation.

èLorsqu'il n'y a plus qu'un seul domaine (fig.2.d), l'aimantation augmente faiblement par rotation du moment magnétique venant s'aligner sur H ( fig.2.e); nous décrivons de manière quasi réversible la partie A₂A₃ du graphe.

èEnfin l'aimantation ne peut plus augmenter et l'augmentation de B = µ_o.(J+H) est due uniquement à celle de H; nous dirons que le matériau est saturé ( partie A₃A₄ du graphe).

.

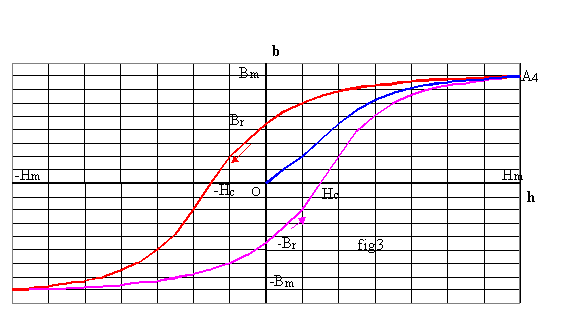
3.3 Cycle d'hystérésis d'un matériau ferromagnétiqu

Dès que les points d'épinglage cèdent, les phénomènes d'aimantation deviennent irréversibles. Ayant décrit la courbe de première aimantation OA₄, faisons décroître l'excitation H. Le champ décroît moins vite qu'il n'a augmenté en raison du couplage des moments qui tend à maintenir l'orientation précédente. Lorsque nous annulons l'excitation, le matériau reste aimanté avec un champ B_r dit champ rémanent. Pour annuler l'aimantation, il faut inverser l'excitation jusqu'à la valeur -H_c dite excitation coercitive. En faisant décroître l'excitation jusqu'à -H_m , nous obtenons un point symétrique de A₄ par rapport à l'origine.

En faisant de nouveau croître l'excitation de -H_m à H_m , nous décrivons une branche symétrique de la précédente.

Le graphe B (H) ainsi obtenu est dit cycle d'hystérésis.

L'hystérésis est un phénomène général en physique; nous disons qu'une propriété d'un système présente un phénomène d'hystérésis chaque fois que l'état du système dépend des variables d'état mais aussi de l'état initial. Ainsi l'aimantation du matériau dépend de l'excitation imposée mais aussi de l'état magnétique antérieur; par exemple H = 0 donne B = 0 si le matériau était préalablement désaimanté, B = B_r si on a annulé H à partir d'une valeur antérieure positive et B = -B_r si on a annulé H à partir d'une valeur antérieure négative.

3.4 Perméabilités relatives

Suivant l'utilisation du matériau nous pouvons utiliser différentes définitions de la perméabilité:

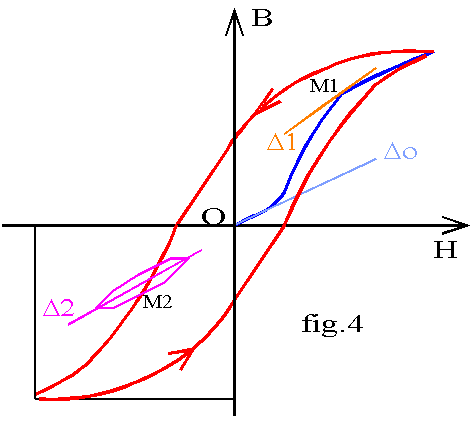
èpour des excitations de faible amplitude, le cycle d'hystérésis s'écarte peu de la courbe de première aimantation. Soit D_o la tangente à l'origine à ce graphe et a_o la pente de cette droite; nous appelons perméabilité relative initiale la quantité µ_ri = a_o / µ_o . Cette perméabilité varie de 10³ à 10⁵. suivant les matériaux.

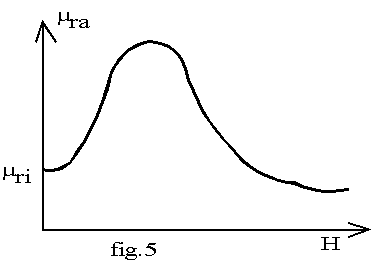
èpour des excitations plaçant le point de fonctionnement M₁ dans la partie non linéaire de la courbe de première aimantation, la pente a₁ de la tangente D₁ définit la perméabilité relative d'amplitude µ_ra = a₁/µ_o . Cette perméabilité évolue en fonction de l'excitation suivant le graphe de la fig.5; sa valeur maximale varie de 10⁴ à 5.10⁵.; elle est utilisée pour caractériser les circuits magnétisés par un courant alternatif basse fréquence.

èSi nous créons une excitation continue H, plaçant le point de fonctionnement en M₂ et si nous lui superposons une excitation alternative h d'amplitude faible devant H, le point de fonctionnement décrit un cycle d'hystéréris local autour de la droite D₂ de pente a₂ la perméabilité relative différentielle est µ_rd = a₂/µ_o . Cette perméabilité est utilisée pour le calcul des inductances de filtrage. Lorsque l'amplitude h de la composante alternative tend vers 0, la perméabilité différentielle tend vers la perméabilité relative réversible µ_rr .

.

4 pertes magnétiques

4.1 Pertes par hystérésis

Lorsque nous décrivons un cycle d'hystérésis, l'aimantation est plus forte pour les valeurs décroissantes de l'excitation que pour les valeurs croissantes; en démagnétisant un circuit, nous ne pouvons donc pas récupérer toute l'énergie nécessaire à la magnétisation; à chaque cycle décrit, nous devons fournir à l'unité de volume du matériau l'énergie w_h =¦ b.dh; cette intégrale représente l'aire du cycle d'hystérésis. Si l'excitation est de fréquence f, un cycle est décrit en T = 1/f et la puissance perdue est p_h = w_h / T = f.w_h . Pour un échantillon de volume V , la puissance perdue est P_h = V .f .w_h ; cette puissance est dite de pertes par hystérésis.

4.2 Pertes par courant de Foucault

Lorsqu'un échantillon est soumis à un champ magnétique alternatif d'amplitude B_m et de fréquence f, il se crée dans le matériau des courants induits; ces courants dits courants de Foucault circulent dans des plans perpendiculaires au champ (fig.6). Ces courants provoquent des pertes par effet Joule dans le volume du noyau. Par unité de volume, la puissance perdue est p_cF = K.B_m^².f ^²/r , r étant la résistivité du matériau. Dans un échantillon, de volume V , les pertes par courants de Foucault sont P_cF = V .p_cF .

Dans la majorité des cas, ces pertes sont nuisibles et nous cherchons à les réduire; pour cela nous pouvons:

augmenter la résistivité du matériau ; par exemple pour le fer de résistivité r = 10^-7 W.m, l'addition de silicium permet de multiplier la résistivité par un nombre allant de 4 à 8. Pour les applications hautes fréquences, nous utilisons des ferrites de forte résistivité : r = 0,1 à 10 W.m.

On diminue ainsi la section conductrice donc on augmente la résistance électrique.

Les courants de Foucault ont quelques applications pratiques

freinage électromagnétique : si le champ est fixe et le matériau mobile, il apparaît des courants d'amplitude proportionnelle à la vitesse de déplacement; d'après la loi de Lenz, ces courants vont créer des forces s'opposant au déplacement. Ce mode de freinage sans contact permet un freinage efficace aux vitesses élevées sans usure du frein et sans dégradation de freinage avec l'élévation de température; il est utilisé dans les ralentisseurs pour les poids lourds.

4.3 Pertes magnétiques

L'ensemble des pertes par hystérésis et par courant de Foucault constitue les pertes magnétiques ou pertes dans le fer. Ces pertes dépendent du matériau, du champ maximal et de sa fréquence.

Nous utilisons des formules empiriques pour les calculer :

èles pertes par hystérésis sont données pour 1 kg de matériau par la formule de Steinmetz , les coefficients h_h et a sont fonction du matériau. Pour les tôles de fer au silicium, h_h varie de 5.10^-4 à 4.10^-3 et a de 1,6 à 2.

èles pertes par courants de Foucault sont données pour 1 kg de matériau par la formule :, le coefficient h_F est fonction du matériau et e est l'épaisseur des tôles.

.Les pertes dans le fer p_fer = p_h + p_cF sont d'environ 0,5 à 2 W.kg^-1 à f = 50 Hz et B_max = 1 T pour les tôles de fer usuelles et 50 W.kg^-1 à f = 10 kHz et B_max = 0,2 T pour les ferrites.

.

5 lois des milieux magnétiques

Les lois du magnétisme dans le vide sont modifiées par la présence d'un matériau magnétique. Nous utilisons les lois suivantes :

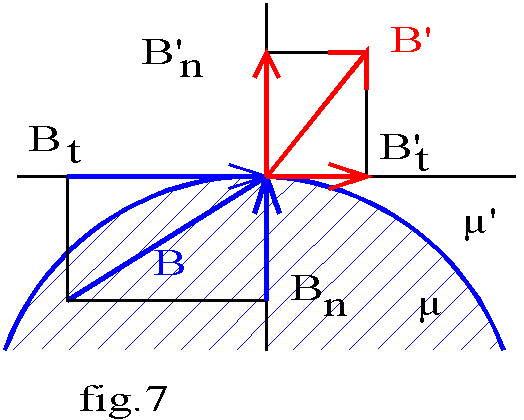
èlors du passage d'un matériau à un autre, le champ est modifié comme suit (fig.7):

la composante normale se conserve : B'_n = B_n