Exercice 1 : On étudie le système ci-dessous :trois fils rectilignes de longueur infinie coupent le plan de figure en O1,O2 et O3
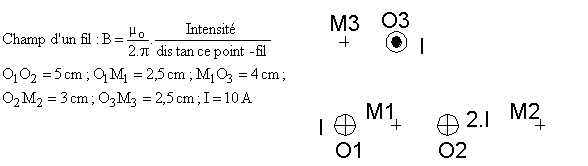 |
| Au point M1 dessiner les champs créés par les trois fils et le champ résultant. |
Appliquer la règle d'Ampère pour trouver le sens et la direction de chaque champ.
Calculer son module avec la formule ci-dessus
Ajouter les trois vecteurs champs
Aide |
|
| Au point M2 dessiner les champs créés par les trois fils et le champ résultant. |
|
| Au point M3 dessiner les champs créés par les trois fils et le champ résultant. |
|
| Représenter au point O3 le champ des fils O1 et O2; représenter et calculer les forces exercées par ces champs sur L = 1m du fil O3. Calculer la force résultante |
Appliquer la règle d'Ampère puis celle des trois doigts
Aide |
B1= 42,4µT ; B2 = 85 µT
F1 = 424 µN ; F2 = 850 µN ;
F =1104 µN
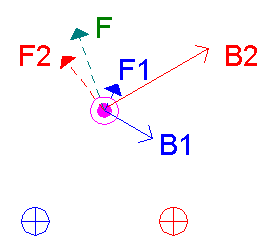
Réponse |
Exercice 2 : on étudie le champ du système suivant
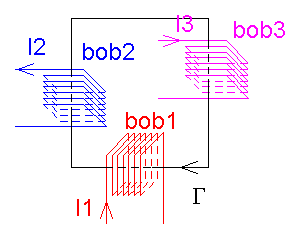
Bobine 1 : I1 = 25 A ; N1 = 20 spires ; Bobine 2 : I2 = 45 A ; N2 = 5 spires ;
Bobine 3 : I3 = 1,5 A ; N3 = 350 spires ; |
| Déterminer les faces Nord et Sud de chaque bobine |
|
| Calculer la circulation du champ sur le parcours G |
Appliquer le théorème d'Ampère
Aide |
C=µo(N1.I1-N2.I2-N3.I3)
C = -0,000 14 USI
Réponse |
Exercice 3 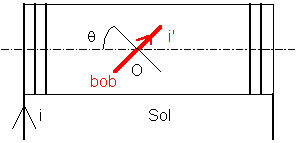
On étudie le système ci-dessus :
un solénoïde "Sol" de diamètre D = 12 cm et de longueur l = 50 cm comportant N = 400 spires
et une bobine plate "bob" de rayon r' = 4 cm comportant N' = 10 000 spires |
| Représenter la direction et le sens du champ B créé en O par le solénoïde. |
Appliquer la règle du tire-bouchon
Aide |
B horizontal orienté de la droite vers la gauche
Réponse |
| On pose B = k. i; calculer k en supposant le solénoïde de longueur infinie. |
Voir formule dans le cours
Aide |
B=µo.(N/l).i
k = 0,001 T/A
Réponse |
| On suppose le champ B uniforme à l'intérieur du solénoïde. Calculer le flux de B à travers une spire du solénoïde. En déduire l'inductance propre du solénoïde. |
S = p.D²/4 ; j = B.S = 11,3.i µWb
Fp = N.j = 4,52.i mWb donc L = Fp/i = 4,52 mH
Réponse |
| Orienter la normale à la bobine et exprimer en fonction de i et de q, le flux créé par B à travers la bobine. |
Normale orientée du bas vers le haut
F' = N'.S'.B.cosq = k.N'.S'.i.cosq =50,3.i.cosq mWb
Réponse |
| Exprimer l'inductance mutuelle de "Sol" et de "bob". Calculer sa valeur maximale. |
M = F'/ i = 50,3.cosq mH
Mmax = 60,3 mH
Réponse |
| Si la bobine est libre de tourner autour d'un axe perpendiculaire en O au plan de figure, représenter sa position d'équilibre stable |
Appliquer la règle du flux maximum
Aide |
|
| Pour I = 10 A et I' = 0,5 A, calculer le travail des forces électromagnétiques pour une rotation de la bobine de 1/2 tour à partir de la position d'équilibre |
Appliquer le théorème de Maxwell
Aide |
F'1= k.N'.S'.i.cos(0) = 503 mWb
F'2= k.N'.S'.i.cos(180) = -503 mWb
W = i'.( F'2-F'1 ) = -0,503 J
Réponse |
On fait tourner la bobine "bob" à la vitesse n = 1 000 tr/min; exprimer en fonction du temps la f.é.m. e' induite dans la bobine.
Pour I = 8 A, calculer sa valeur efficace et sa fréquence. |
j' = k.N'.S'.i.cosq =0,0503.i.cosq Wb
q = w.t avec w = 2.p.n/60 = 105 rd/s
e' = -dj' /dt = 0,0503.i.w.sin(w.t)
E' = 14,9 V ; f ' = n/60 = 16,7 Hz
Réponse
|
On fixe q = 30° et on alimente le solénoïde par un courant i sinusoïdal de fréquence
f = 50 Hz et de valeur efficace I = 5 A. Exprimer en fonction du temps la f.é.m. e' induite dans la bobine; calculer sa valeur efficace et sa fréquence.
|
j'= k.N'.S'.i.cos(30) =43,6.I.Ö2.sin(2.p.f.t) mWb
j'=0,308.sin(2.p.f.t) Wb
e' = -dj'/dt = 0,308.(2.p.f).cos(2.p.f.t)
E' = 68,4 V ; f' = f = 50 Hz
Réponse |
Exercice 4 : on étudie le système ci-dessous
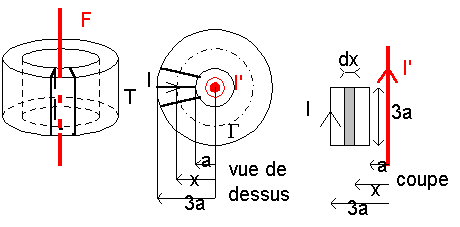
T est un tore portant un bobinage de N = 200 spires uniformément réparties et parcourues par un courant i ; F est un fil rectiligne de longueur infinie, parcouru par un courant i'. On donne a = 10 cm |
Étude du tore |
| On considère le cercle F de rayon x. Montrer qu'en tout point du cercle, le champ B(x) créé par le tore est tangent au cercle et constant en module |
Le champ respecte les symétries du circuit
Réponse |
| Exprimer en fonction de B('x) et x la circulation du champ sur G |
|
| En appliquant le théorème d'Ampère au contour G, donner l'expression de B(x) en fonction de N, i et x |
C=µo.N.i B = µo.N.i/(2.p.x)
Réponse |
| En utilisant la vue en coupe, exprimer le flux dj de B à travers la surface grisée |
dj = B.dS.cos(0)=B(x).3a.dx
dj = (3.a.µo.N/2.p).i.dx/x
Réponse |
| En déduire le flux de B à travers une spire |
Il faut intégrer dj sur toute la surface de la spire
donc intégrer par rapport à x variant de a à 3.a
Aide |
|
| Calculer l'inductance propre du bobinage du tore |
Fp=N.F : L = Fp / i
L = 2,64 mH
Réponse |
Effet du fil sur le tore |
Exprimer le champ B' créé par le fil à distance x de celui-ci.
Représenter son sens et sa direction. |
B'=µo.i'/(2.p.x)
B' est perpendiculaire à la spire et dirigé vers l'avant sur la figure en coupe
Réponse |
| Exprimer le flux j' créé par B' à travers un spire du tore |
Utiliser la même méthode que pour le flux propre :
calculer le flux à travers la surface grisée puis intégrer
Aide |
dj' = B'.dS.cos(180)=-B'(x).3a.dx
dj' = -(µo/2.p).i'.dx/x
j' = -(µo.Ln(3)/2.p).i'
Réponse |
| Calculer l'inductance mutuelle M entre le tore et le fil |
F' = N.j' ; M = F'/ i'
M =- µo.N.Ln(3)/2.p = -44 µH
Réponse |
| Le fil est parcouru par un courant sinusoïdal de fréquence f' = 50 Hz et de valeur efficace I' = 150 A. Calculer la valeur efficace de la f.é.m. induite dans le bobinage du tore |
F' = M .i' ; e =-dF'/dt = -M.di'/dt
E = M.I'.2.p.f' = 2,07 V
Réponse |
| Le bobinage du tore est mis en court-circuit. Calculer l'intensité efficace I' dans le tore. On donne la résistance de la bobine r = 0,8 W. |
Calculer l'impédance de la bobine (r,L)
Aide |
Z = Ö[r² +(L.w)²]= 1,15 W ; I = E / Z = 1,8 A
Réponse |
| Quelle peut-être l'utilisation d'un tel système |
Mesure d'un courant important avec isolement du circuit de mesure : pince ampèremétrique
Réponse |