Électrotechnique
xxxxModule 1 : xxx "Magnétisme" |
Chapitre 1.1
Magnétisme dans le vide |
Un aimant permanent est un corps qui a la propriété d'attirer le fer. On distingue
v les aimants naturels tels la magnétite qui sont intrinsèquement aimantés; ces corps sont connus depuis l'antiquité et sont utilisés depuis le XIème siècle dans les boussoles.
v les aimants artificiels qui ne prennent leurs propriétés magnétiques qu'après un traitement préalable.
Sur un aimant, la limaille de fer n'est attirée que par des zones délimitées appelées pôles. La droite joignant les pôles s'oriente naturellement suivant l'axe géographique Nord - Sud, d'où les noms de pôles Nord et Sud donnés à ces zones. Les pôles ne peuvent exister que par paires Nord - Sud.
Les aimants exercent entre eux des forces magnétiques :
v deux pôles de même nom se repoussentv deux pôles de noms contraires s'attirent.
On appelle champ magnétique toute région de l'espace où un aimant est soumis à une force magnétique. Une petite aiguille aimantée sert à tester l'existence d'un champ.
En tout point M d'un champ est défini le vecteur champ magnétique ![]() :
:
v sa direction et son sens sont donnés par l'axe Sud - Nord de l'aiguille aimantéev son intensité est fonction de la force exercée sur l'aiguille; elle s'exprime en tesla (T)
Par exemple, le champ magnétique terrestre, approximativement dirigé vers le pôle Nord, est de l'ordre de 0,5 mT; celui d'un aimant est de l'ordre de 0,1 T; dans les machines on crée des champs de l'ordre du tesla
Le champ magnétique peut être décrit en traçant ses lignes de champ, c'est à dire des courbes telles qu'en tout point le vecteur champ leur soit tangent et orientées dans le sens du vecteur ![]() . Ces lignes de champ peuvent être matérialisées avec de la limaille de fer. La fig.1 donne l'exemple des lignes de champ d'un aimant "en U".
. Ces lignes de champ peuvent être matérialisées avec de la limaille de fer. La fig.1 donne l'exemple des lignes de champ d'un aimant "en U".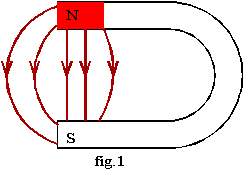
3 Champ magnétique créé par un couranT
3.1 Expérience d'Oersted
En plaçant une aiguille aimantée au voisinage d'un conducteur parcouru par un courant continu, on constate l'existence d'un champ magnétique.
Ce champ :
v a une intensité proportionnelle à l'intensité du courantv diminue lorsqu'on s'éloigne du conducteurv a une direction et un sens donnés par la règle du bonhomme d'Ampère :Un observateur couché sur le conducteur, le courant allant de ses pieds vers sa tête, regarde le point M où l'on veut déterminer le champ; il tend son bras gauche dans le plan de son corps pour déterminer la direction et le sens de
.
Pour plus de commodité, on peut utiliser la main droite : la paume représente la face de l'observateur, le bout des doigts sa tête et le pouce son bras gauche.
Pour les circuits fermés, on peut aussi utiliser le "tire-bouchon de Maxwell" :
Un tire-bouchon placé au point M suivant un axe perpendiculaire au plan du circuit tourne dans le sens du courant; son sens de progression (visser ou dévisser) donne le sens du champ en M.
3.2 Loi de Biot et Savart
Soit un élément de conducteur de longueur dl, parcouru par le courant d'intensité I et placé au point O. Cet élément de courant crée en un point M le champ élémentaire :

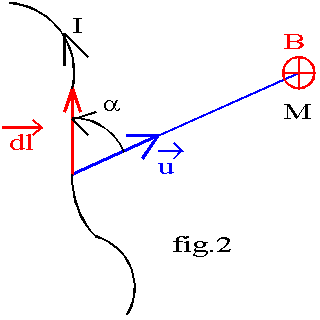
4.1 Circulation du champ magnétique
Soit un point A placé dans un champ magnétique; le champ en ce point est ![]() ; pour un déplacement
; pour un déplacement ![]() de A, on appelle circulation du champ :
de A, on appelle circulation du champ :
![]() .
.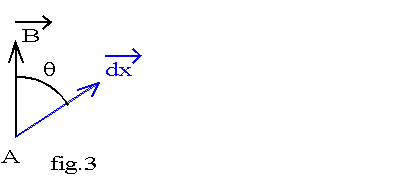
La circulation du champ est analogue au travail d'une force.
4.2 Faces d'un circuit
Soit un circuit plan parcouru par un courant I; la normale ![]() est orientée en utilisant la règle du tire-bouchon de Maxwell.
est orientée en utilisant la règle du tire-bouchon de Maxwell.
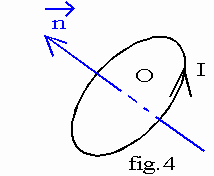
Par analogie avec les aimants, on distingue :
v la face Nord du circuit, face par laquelle sort 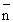 ; un observateur placé devant la face Nord voit le courant tourner dans le sens direct.
; un observateur placé devant la face Nord voit le courant tourner dans le sens direct.
v la face Sud du circuit, face par laquelle entre 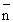
Un observateur placé devant la face Nord voit le courant tourner dans le sens des aiguilles de montre.
4.3 Théorème d'Ampère
La circulation du champ sur un parcours fermé G est égale à µo fois la somme algébrique des courants enlacés.
Un courant est dit enlacé chaque fois que le parcours G traverse le plan du circuit; il est compté positivement si G traverse de la face Sud vers la face Nord et négativement si G traverse de la face Nord vers la face Sud.
.
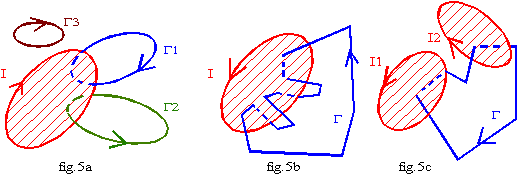
Sur la fig.5a : circulation sur G1 : C1 = µo.I , sur G2 : C2 = -µo.I ; sur G3 : C3 = 0.
Sur la fig.5b : circulation sur G : C = 2.µo.I.
Sur la fig.5c : circulation sur G : C = -µo.I1 + µo.I2 .
4.4 Application
Le théorème d'Ampère peut permettre de calculer rapidement un champ magnétique.
Exemeple 1
Soit un fil de longueur infinie parcourue par le courant I. Par raison de symétrie, le champ B ne dépend que de la distance au fil.
Prenons comme parcours G, le cercle de rayon a, ayant le fil pour axe, orienté dans le sens direct. ![]() de module constant est tangent au cercle ; la circulation sur G est par définition :
de module constant est tangent au cercle ; la circulation sur G est par définition :
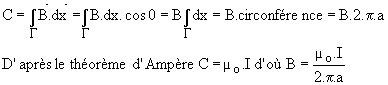
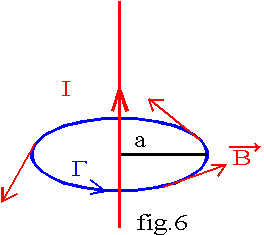
Exemple 2
Soit un solénoïde, bobine de longueur grande devant son diamètre. On constate que le champ est uniforme à l'intérieur, c'est à dire que
est constant et qu'il est parallèle à l'axe de la bobine.
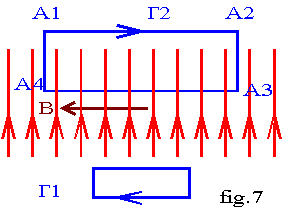
Sur le parcours extérieur G1, la circulation est nulle puisqu'aucun courant n'est bouclé. Le champ extérieur est donc nul.
Sur le parcours G2, la circulation se décompose en 4
sur A1A2, B est nul donc C1 = 0 sur A2A3
sur A4A1, q = 90° donc C2 = C4 = 0
sur A3A4, B est constant et q = 0 donc C3 = B.L avec L = A3A4.La circulation totale est donc C = B.L. Soit n le nombre de spires par unité de longueur. Le parcours G2 boucle N = n.L spires donc C = µo.n.L.I; nous en déduisons B = µo.n.I.
5.1 Loi de Laplace
Soit un élément de circuit de longueur dl, parcouru par un courant I et placé en un point M d'un champ magnétique ![]() ; ce conducteur est soumis à la force
; ce conducteur est soumis à la force ![]() donnée par la loi de Laplace :
donnée par la loi de Laplace :
![]() .
.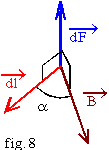
Cette force est orthogonale au circuit et à B.
Le sens et la direction de la force sont donnés par :
règle des trois doigts : plaçons le pouce de la main droite sur le conducteur, dans le sens du courant I, l'index tendu dans le même plan suivant le champ magnétique; le majeur tendu perpendiculairement au plan pouce - index donne la direction et le sens de la force.
5.2 Couple électromagnétique
On démontre que :
Un circuit électrique plan de surface S, parcouru par un courant d'intensité I et placé dans un champ uniforme B est soumis à un ensemble de forces électromagnétiques de résultante nulle et à un couple de moment T :
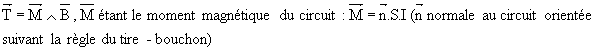
Vérifions ce résultat sur un exemple simple: un cadre rectangulaire vertical est placé dans un champ magnétique uniforme horizontal.
Calculons par la loi de Laplace les forces sur les quatre côtés :
.
sur MN : la force 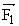 est verticale, dirigée vers le haut de module F1= B.I.MN.|sin (a+p/2)|
est verticale, dirigée vers le haut de module F1= B.I.MN.|sin (a+p/2)|
sur NP : la force ![]() est horizontale, de module F2= B.I.NP.|sin (p/2)|
est horizontale, de module F2= B.I.NP.|sin (p/2)|
sur PQ : la force ![]() est verticale, dirigée vers le bas de module F3= B.I.MN.|sin (a+p/2)|
est verticale, dirigée vers le bas de module F3= B.I.MN.|sin (a+p/2)|
Les forces s'annulent deux à deux ( fig.9a) donc la résultante et nulle.
![]() et
et ![]() sont directement opposées donc ne créent pas de couple; les forces
sont directement opposées donc ne créent pas de couple; les forces ![]() et
et ![]() parallèles mais de droites d'action différentes créent un couple de moment T = F2.HM ; avec HM = MN.sin a, il vient
parallèles mais de droites d'action différentes créent un couple de moment T = F2.HM ; avec HM = MN.sin a, il vient
T = B.I.NP.MN.sin a ; MN.NP est la surface du cadre. Nous obtenons donc :
6.1 Définition
.Soit une surface dS orientée par son vecteur normal ![]() et placée en un point où le champ magnétique est
et placée en un point où le champ magnétique est ![]() . Le flux magnétique F à travers la surface est le produit scalaire F=
. Le flux magnétique F à travers la surface est le produit scalaire F=![]() .
.![]() .dS =B.dS.cos q avec
.dS =B.dS.cos q avec
q = (![]() ,
,![]() ).
).
Le flux est souvent utilisé à la place du champ car c'est une grandeur scalaire plus facile à manipuler qu'une grandeur vectorielle.
Le flux s'exprime en weber (symbole Wb) : 1 Wb = 1 T * 1 m²
6.2 Travail des forces électromagnétiques
.Un conducteur placé dans un champ magnétique est soumis à une force; lorsqu'on déplace le circuit, cette force produit un travail W; ce travail peut être calculé à partir du flux.
6.2.1 Première expression
Etudions le système de la fig.10a : un conducteur MN, parcouru par un courant I, glisse sur des rails horizontaux; l'ensemble est placé dans un champ magnétique uniforme vertical.
Le conducteur est soumis à une force ![]() horizontale, dirigée vers la droite et de module F = B.I.MN. Sous l'effet de cette force, le conducteur se déplace; pour le trajet de MN en M'N', le travail de la force est W=F.MM' = B.I.MN.MM'; le produit MN.MM' représente la surface hachurée S balayée par le conducteur lors de son déplacement; W = I.B.S; B.S est le flux F à travers la surface balayée, il vient donc W=I.F. Ce flux F prend le nom de flux coupé.
horizontale, dirigée vers la droite et de module F = B.I.MN. Sous l'effet de cette force, le conducteur se déplace; pour le trajet de MN en M'N', le travail de la force est W=F.MM' = B.I.MN.MM'; le produit MN.MM' représente la surface hachurée S balayée par le conducteur lors de son déplacement; W = I.B.S; B.S est le flux F à travers la surface balayée, il vient donc W=I.F. Ce flux F prend le nom de flux coupé.
Ce résultat est valable quelle que soit la forme du circuit.
Théorème de Maxwell : le travail des forces électromagnétiques d'un circuit d'intensité I, placé dans un champ magnétique est égal au produit de l'intensité par le flux coupé par le circuit lors de son déplacement.
.
6.2.2 Deuxième forme
Lorsque le circuit est de forme complexe, le calcul du flux coupé peut être difficile voire impossible. Sur la fig.10b, on note que la surface balayée est la différence de la surface finale du circuit (hachurée) et de celle initiale (quadrillée). Le flux coupé est donc la différence des flux final et initial à travers le circuit :
W = I.DF = I.(Ff-Fi).
Théorème de Maxwell : le travail des forces électromagnétiques d'un circuit d'intensité I, placé dans un champ magnétique est égal au produit de l'intensité par la variation du flux à travers le circuit entre les positions finale et initiale.
6.3 Théorème du flux maximal
.Lorsqu'un circuit parcouru par un courant I est placé dans un champ magnétique, il y se place généralement dans une position d'équilibre.
Si cette position d'équilibre est stable, lorsque nous tentons d'écarter le circuit de cette position, les forces électromagnétiques s'opposent au déplacement et donc créent un travail résistant; d'après la deuxième forme du théorème de Maxwell W = I.DF < 0 implique DF<0 donc un flux décroissant lors du déplacement. Le flux était donc maximal à l'équilibre.
Si cette position d'équilibre est instable, lorsque nous tentons d'écarter le circuit de cette position, l'équilibre est rompu; les forces électromagnétiques sont motrices et donc créent un travail moteur; d'après la deuxième forme du théorème de Maxwell W = I.DF > 0 implique DF>0 donc un flux croissant lors du déplacement. Le flux était donc minimal à l'équilibre.
Règle du flux maximal : un circuit électrique placé dans un champ magnétique prend une position d'équilibre telle que le flux soit extremum dans cette position. Si le flux est maximal, l'équilibre est stable et si le flux est minimal, l'équilibre est instable.
7.1 Mise en évidence
.Prenons une bobine fermée sur une résistance R; choisissons arbitrairement le sens du courant dans la bobine; nous en déduisons le sens de la normale ![]() ; plaçons un aimant droit suivant l'axe de la bobine; si nous déplaçons l'aimant vers la bobine, nous constatons l'apparition d'un courant i positif d'autant plus élevé que le déplacement est rapide. Si nous éloignons l'aimant, nous constatons l'apparition d'un courant i négatif. Le courant n'existe que durant les déplacements. Ce courant est créé par une f.é.m de même sens dans la bobine.
; plaçons un aimant droit suivant l'axe de la bobine; si nous déplaçons l'aimant vers la bobine, nous constatons l'apparition d'un courant i positif d'autant plus élevé que le déplacement est rapide. Si nous éloignons l'aimant, nous constatons l'apparition d'un courant i négatif. Le courant n'existe que durant les déplacements. Ce courant est créé par une f.é.m de même sens dans la bobine.
Le champ magnétique de l'aimant crée un flux négatif à travers la bobine; en approchant l'aimant on augmente le champ magnétique dans la bobine donc la valeur absolue du flux; compte tenu du signe négatif, le flux diminue en valeur relative. La variation du flux induit un courant dans la bobine. Ce courant crée à son tour un champ magnétique; s'il est positif, le champ a le sens de la normale et la bobine présente sa face Nord au pôle Nord de l'aimant. Deux pôles de même nom se repoussent donc le courant induit s'oppose au déplacement de l'aimant. Nous pouvons énoncer :
Loi de Lenz : la variation du flux à travers un circuit électrique induit une f.é.m. Cette f.é.m a un sens tel qu'elle s'oppose par ses effets à la cause de variation du flux.
7.2 Expression de la f.é.m induite
.
Reprenons le système des rails et fermons le circuit sur une résistance. 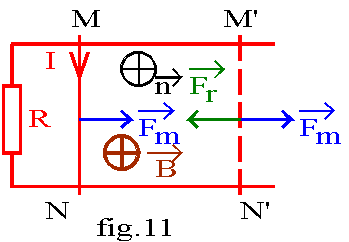
Appliquons à la barre MN une force motrice ![]() dirigée vers la droite; sous l'effet de cette force, MN se déplace vers la droite, augmentant la surface du circuit donc le flux; la variation du flux induit une f.é.m donc un courant I; l'interaction entre I et B crée une force électromagnétique Fr = B.I.MN ; d'après la loi de Lenz, cette force doit s'opposer au déplacement donc est dirigée vers la gauche.
dirigée vers la droite; sous l'effet de cette force, MN se déplace vers la droite, augmentant la surface du circuit donc le flux; la variation du flux induit une f.é.m donc un courant I; l'interaction entre I et B crée une force électromagnétique Fr = B.I.MN ; d'après la loi de Lenz, cette force doit s'opposer au déplacement donc est dirigée vers la gauche.
Le courant I est donc négatif ( de bas en haut dans MN). La force motrice crée une accélération constante donc une vitesse v croissante. Plus v augmente, plus le flux varie vite donc plus |I| augmente; Fr augmente donc l'accélération proportionnelle à Fm - Fr diminue.
Pour Fr = Fm , l'accélération devient nulle et la vitesse constante.
Pour un déplacement élémentaire dx de MN, la surface du circuit augmente de dS = MN.dx et le flux de
dF = B.dS ; pour ce même déplacement, le travail de la force motrice égale à la force résistance est
dWm = Fm.dx = Fr.dx = B.I.MN.dx = B.I.dS = I.dF. cette énergie mécanique est convertie en énergie électrique par la f.é.m induite E ; l'énergie électrique produite est dWe = E.I.dt ; la conservation de l'énergie implique dWm+ dWe = 0 soit E.I.dt = -I.dF
Nous en déduisons E = - dF / dt ou E = -B.MN.dx/dt = -B.MN.v.
Ce résultat peut être étendu à un circuit quelconque:
Loi de Faraday : la f.é.m. induite dans un circuit par la variation du flux est e = - dF/dt. Le sens positif de e est celui dans lequel est orienté le courant dans le circuit.
8.1 Inductance propre d'un circuit
.Lorsqu'un circuit électrique est parcouru par un courant, ce courant crée un champ magnétique
; ce champ crée un flux à travers le circuit créateur, appelé flux propre. Les règles d'orientation de
et de la normale
étant les mêmes (règle du tire-bouchon), les deux vecteurs ont le même sens donc le flux propre est toujours positif.
Le champ créé par un circuit est proportionnel au courant I; nous avons donc F = L.I. La constante L est toujours positive et ne dépend que de la géométrie du circuit; nous l'appelons coefficient d'inductance propre du circuit ou en abrégé inductance du circuit.
L'inductance s'exprime en henry (symbole H) : 1 H = 1 Wb / 1 A.
8.2 F.é.m. d'auto-induction
Au paragraphe 7, nous n'avons fait aucune hypothèse sur la source du flux induisant la f.é.m par sa variation. La loi de Faraday s'applique donc au flux propre. La variation du flux propre induit une f.é.m. dite d'auto-induction e = -dFp /dt = -d(L.i)/dt. Pour un circuit indéformable, l'inductance est constante donc e = - L.di/dt. Cette f.é.m. est orientée dans le sens du courant; si nous étudions le circuit avec une convention récepteur, la d.d.p. v doit être orientée en sens inverse de l'intensité; il vient v = -e = L.di/dt.
8.3 Effets de l'auto-induction
Etudions le fonctionnement du circuit de la fig.12.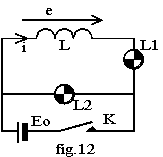
Supposons K ouvert et i = 0; fermons K, la lampe L2 soumise à la d.d.p. Eo s'éclaire instantanément. Le courant i dans la bobine augmente donc le flux propre augmente et la f.é.m. d'auto-induction e = - Ldi/dt est négative. Cette f.é.m. s'oppose donc à l'augmentation du courant la lampe L1 va donc s'éclairer progressivement.
Lorsque i atteint sa valeur continue de régime permanent, e s'annule donc L1 soumise à la d.d.p. Eo éclaire comme L2.
Ouvrons alors K; le circuit n'étant plus alimenté i va s'annuler; i diminuant, la f.é.m. e est positive et alimente les deux lampes en série; la décroissance du courant étant rapide, les deux lampes s'éclairent fortement puis s'éteignent simultanément.
Si nous débranchons la lampe L2, lors de l'ouverture de K, la bobine est mise en circuit ouvert; le courant doit donc s'annuler en un temps très bref égal au temps de coupure de l'interrupteur; par exemple si L = 1 H et I = 1 A, pour un temps de coupure de 1 ms, la f.é.m. induite vaut e = -L.di/dt = -1 * 1 /0,001 = 1 kV. Cette tension élevée est suffisante pour ioniser l'air entre les plots de l'interrupteur et amorcer un arc, dit d'extra-rupture.
L'ouverture d'un circuit inductif peut créer des surtensions dangereuses pour les composants du circuit, pour l'opérateur; cette surtension peut détériorer l'interrupteur s'il n'est pas adapté.
.
Soit deux circuits :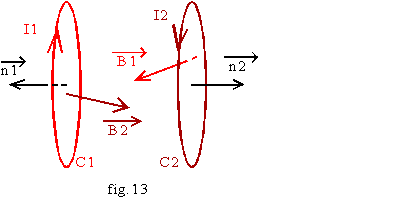
C1 parcouru par le courant I1 crée le champ magnétique B1 = k1.I1
C2 parcouru par le courant I2 crée le champ magnétique B2 = k2.I2
C1 crée à travers C2 un flux F12 = k12.B1 = K.I1; la constante K dépend de la géométrie des deux circuits et de leur position relative. C2 crée à travers C1 un flux F21 = k21.B2 = K'.I2; la constante K' dépend de la géométrie des deux circuits et de leur position relative.Les paramètres fixant K et K' étant identiques, leurs valeurs sont égales.
Le coefficient d'inductance mutuelle M entre deux circuits est égal au quotient du flux créé par un circuit dans l'autre par le courant créant le flux : M = F12 / I1 = F21 / I2 .
Contrairement à l'inductance propre L, ce coefficient M peut être de signe quelconque; par exemple, sur la fig.13, M < 0.
La variation du courant I1 induit une variation du flux donc crée une f.é.m induite
e12 = -dF12 /dt = -M.d I1/dt.
Lorsqu'on veut schématiser deux bobines couplées magnétiquement, on peut utiliser la représentation de la fig.14. La position des points permet de déterminer le signe de M :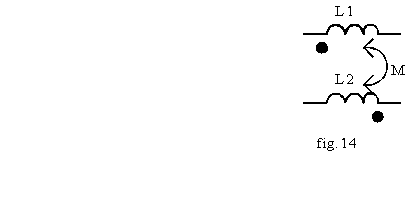
si l'orientation des courants dans L1 et L2 est la même par rapport aux deux points ( les deux courants entrent ou sortent dans les bobines par le côté où se trouve le point ) alors M > 0
si l'orientation des courants dans L1 et L2 est opposée par rapport aux deux points ( un courant entre par le côté repéré par le point, l'autre sort par le côté repéré par le point ) alors M <
Par exemple si les deux courants dans L1 et L2 sont orientés de gauche à droite alors M < 0.