Électrotechnique
x x Module 5: x
"Machine synchrone" |
Chapitre 5.3
Exploitation
|
On étudie une machine synchrone triphasée dont le stator est couplé en étoile. La plaque signalétique porte : 500 tr/ min - 50 Hz - 5,5 kV - 210 kVA. On donne : v la résistance entre deux bornes du stator R's = 4 W
v la caractéristique à vide Cv : f.é.m. par phase Eo en fonction de l'intensité d'excitation Ie, relevée à vitesse nominale
v la réactance synchrone Xs = 70 W
v les coefficients de Potier a = 90 % et l = 25 W
La machine synchrone est excitée par une source séparée et la résistance de son inducteur est Re = 5 W
Cliquez ici pour voir la caractéristique à vide |
|||||||||||||||||||||||||||||||
Dans cet exercice, on utilisera la méthode de Potier Pour mesurer les pertes, on entraîne la machine synchrone par une machine à courant continue utilisée en excitation séparée. Sous tension Ua = 500 V et à la vitesse n = 500 tr/min, on a relevé le courant d'induit Ia de la machine continue coures divers points de fonctionnement: machine continue désaccouplée de toute charge : Ia = 4 A
machine continue entraînant la machine synchrone non excitée : Ia = 19 A machine continue entraînant l'alternateur à vide excité sous Ie :
La résistance d'induit de la machine continue est Ra = 1,1 W et on suppose son couple de pertes de moment constant. |
|||||||||||||||||||||||||||||||
La machine fonctionne en alternateur. Elle alimente sous tension nominale, une charge équilibrée consommant le courant nominal avec un facteur de puissance 0,90 AR. |
|||||||||||||||||||||||||||||||
1.1 Déterminer la valeur du courant d'excitation |
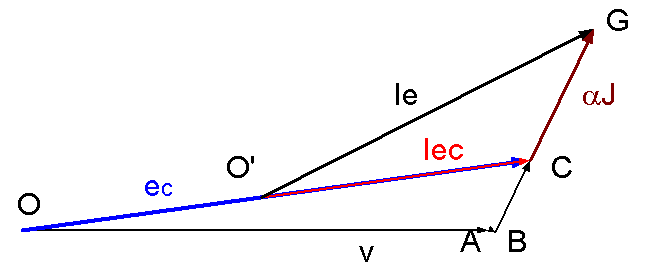
Calculer les grandeurs d'une phase Choisir une échelle de tension en V/cm Dessiner le diagramme de Potier |
V = U / Ö3 = 3 175V ; Inom = Snom/U / Ö3 = 22 A ; J = I = 22 A ; j = 25,84° Echelle b = 250 V/cm ; a = 5 A /cm OA = V/b = 12,7 cm ; AB = Rs.J/b = 0,18 cm ; BC =l.J/b 2,2 cm Ec = b.OC = 3 488 V ; O'C = 37/5 = 7,4 cm ; CG =a.J/a= 3,97 cm ; Ie = a.O'G = 50,8 A
Eo = 16 900 V ; Ie = 2 950 A |
|||||||||||||||||||||||||||||
1.2 Faire le bilan des diverses pertes de la machine |
Le premier essai de la machine continue permet de calculer ses pertes constantes pc = Pem1 Le deuxième essai de MC permet de calculer les pertes mécaniques de MSy : Pem2 = pc+pmec Le troisième essai permet de calculer les pertes fer de MSy : Pem3 = pc+pmec+pfst |
Machine continue seule : Pem = (Ua-Ra.Ia).Ia = 1 982 W = pc ; Tem = Tp = Pem/W = 37,86 Nm Machine continue + machine asynchrone non excitée : Pem = (Ua-Ra.Ia).Ia = 9 103 W ; Pu = Pem - pc = 7 121 W = pmec de MSy Machine continue + Msy à vide excitée sous Ieo = Iec = 37 A : Ia = 50 A Pem = (Ua-Ra.Ia).Ia = 22 250 W ; Pu = Pem - pc = 20 268 W = pmec+pfs de MSy ; pfs = 13 147 W Pertes par effet Joule au stator : pjs = 3.R's.I²/2 = 2 904 W Pertes par effet Joule au rotor : pjr = Re.Ie² = 12 903 W
|
|||||||||||||||||||||||||||||
1.3 Calculer le rendement |
Pu = Ö3.U.I.cos j = 189 kW pertes = pmec + pfs + pjs +pjr = 36,08 kW Pa = Pu + pertes = 225,08 kW h = Pu / Pa = 84 % |
||||||||||||||||||||||||||||||
1.4 Calculer le moment du couple à fournir à la machine |
La machine absorbe Pmec = Pu + pmec + pfst + pjst sur l'arbre (l'excitation est séparée) : Pmec = 212,2 kW T = Pmec /W = 4,05 kNm |
||||||||||||||||||||||||||||||
La machine fonctionne en moteur sous tension et fréquence nominale. La puissance absorbée est constante P = 150 kVA. |
|||||||||||||||||||||||||||||||
2.1 Déterminer la valeur du courant d'excitation pour les trois valeurs du facteur de puissance : 0,71 AR, 1, 0,8 AV |
P = 3.V.J.cosj V = 3,175 kV ; J.cos j = Jactif = 15,75 A.
|
||||||||||||||||||||||||||||||
2.2 Pour chacun des trois points ci-dessus, faire le bilan des pertes |
Les pertes mécaniques sont celles du 1.2 Les pertes fer sont calculées comme au 1.2 pour chaque valeur de Iec |
|
|||||||||||||||||||||||||||||
2.3 Pour chacun des trois points ci-dessus, calculer le rendement et le moment du couple utile |
Pab = P + pjr ; Pu = P - pmec - pjst - pfst ; T = Pu /W
|
||||||||||||||||||||||||||||||
1 Quelle doit être la valeur du courant d'excitation pour qu'après couplage on ait un courant d'induit nul ? |
Il faut avoir Ev = V = 3 175 V soit Ie = 30 A |
||||||||||||||||||||||||||||||
On suppose qu'au moment du couplage, la f.é.m. ev est en phase avec v et que sa valeur efficace est
Ev = 3 kV |
|||||||||||||||||||||||||||||||
2.1 Calculer le courant dans le stator |
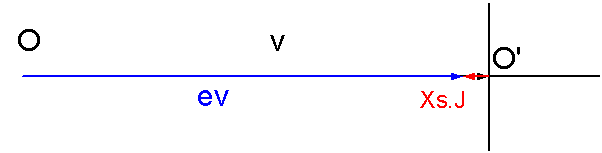
En conventions générateur, on a le diagramme bipolaire ci-dessous :
Xs.J = V - Ev = 175 V ; J = I = 2,51 A |
||||||||||||||||||||||||||||||
2.2 Calculer les puissances active et réactive fournies par la machine |
Suivant le diagramme ci-dessus j = -90° P = 3.V.J.cos j = 0 et Q = 3.V.J.sin j = -23,87 kVAR |
||||||||||||||||||||||||||||||
2.3 Calculer le moment du couple électromagnétique |
Comme on néglige R, Pem + P = 0 donc Tem = 0 |
||||||||||||||||||||||||||||||
On suppose qu'au moment du couplage, la f.é.m. ev est égale à v en valeur efficace mais est en retard de 1/20 de période sur v |
|||||||||||||||||||||||||||||||
3.1 Calculer le courant dans le stator |
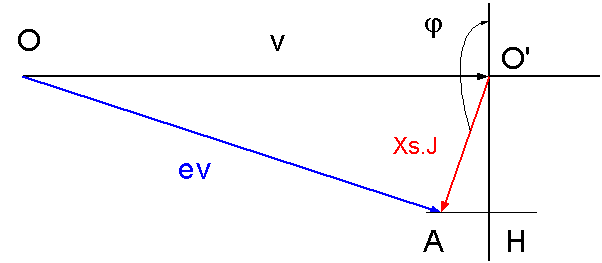
Ev est en retard de 36 ° sur v : diagramme en générateur
Xs.J = 980 V ; J = I = 14 A |
||||||||||||||||||||||||||||||
3.2 Calculer les puissances active et réactive fournies par la machine |
Suivant le diagramme ci-dessus j =-161° P = 3.V.J.cos j = -126 kW Q = 3.V.J.sin j = -43,62 kVAR |
||||||||||||||||||||||||||||||
3.3 Calculer le moment du couple électromagnétique |
Pem = P = Tem.Ws Tem = -2 410 Nm |
||||||||||||||||||||||||||||||
On néglige les pertes de la machine synchrone |
|||||||||||||||||||||||||||||||
1.1 Quelle est la valeur minimale du courant d'excitation pour que la machine fournisse de la puissance réactive |
On a P = 0 et à j < 0 on a arithmétiquement Ev = V + Xs.J il faut donc Ev > V = 3 175 V soit Ie > 29 A |
||||||||||||||||||||||||||||||
1.2 Ie varie de 30 à 60 A. Montrer que le moteur est équivalent à une batterie de condensateurs. Calculer les valeurs minimales et maximale d'un condensateur, en supposant leur couplage en triangle |
Ie = 30 A ; Ev = 3 250 V ; J = (Ev-V)/Xs = 1,1 A ; Q = -3.V.J = -10,1 kVAR Ie = 60 A ; Ev = 4 100 V 13,2 A ; Q = -125,8 kVAR Qc = -3.C.w.U² : 0 ,356 µF < C < 4,41 µF |
||||||||||||||||||||||||||||||
1.3 Le réseau alimente une charge qui consomme 200 kW avec un facteur de puissance 0,8 AR. Quelle doit être la valeur du courant d'excitation pour amener à 0,98 AR le facteur de puissance de l'ensemble. |
cos j = 0,8 AR ; Q = P.tg j = 150 kVAR cos j' = 0,98 AR ; Q' = P.Tg j' = 40,6 kVAR Le moteur absorbe Q" = Q' - Q = -109,4 kVAR ; J = -Q"/3. V = 11,5 A Ev = V + Xs.J = 3 980 V ; Iex = 52 A |
||||||||||||||||||||||||||||||
1.4 Quel est l'intérêt de relever le facteur de puissance ? |
I = P/(3.V.cosj) Sans compensation I = 26,2 A Avec compensation I = 21,4 A I est réduit de 18 % et les pertes de distributions proportionnelles à I² de 33 % |
||||||||||||||||||||||||||||||
On tient compte des pertes décrites dans l'exercice 1; le courant d'excitation est réglé à Ie = 52 A |
|||||||||||||||||||||||||||||||
2.1 Déterminer le courant d'induit, les puissances actives et réactives consommées par la machine synchrone |
le moteur synchrone absorbe Pm = pmec +pjst + pfst d'après l'exercice 1 : pmec = 7 121 W ; pfst sont calculées pour Iex = 52 A soit dans l'essai à vide pour MC : Ia = 74 A Les pertes Joule sont inconnues si on ne connaît pas J; se donner une valeur de J, calculer pjst et Pm; en déduire le facteur de puissance et déterminer Ev ; procéder à plusieurs essais jusqu'à avoir Ev = 3 980 V correspondant à la valeur de Iex = 52 A |
pfst = 28 800 W
|
|||||||||||||||||||||||||||||
2.2 Le moteur synchrone et la charge du 1.3 sont alimentés en parallèle par le réseau; calculer le facteur de puissance de l'ensemble et le courant total en ligne |
P ' = P + Pm = 236 800 W ; Q' = Q + Qm = 40 760 VAR S' = 240 280 VA ; cos j' = P'/S' = 0,986 AR ; I' = S'/Ö3.U = 25,2 A
|
||||||||||||||||||||||||||||||