Untitled Document

Méthode de Potier

Avec les mêmes échelles, nous traçons sur une feuille de papier millimétré la caractéristique à vide Co dans des axes O_ox_o et O_oy_o et sur une feuille de papier calque la caractéristique Ci à J_réac= Cste dans des axes O_ix_i et O_iy_i.

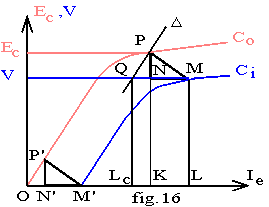
Nous plaçons le calque sur la feuille en superposant les axes puis nous faisons glisser le calque en gardant parallèles les deux systèmes d’axes jusqu’à ce que Ci se superpose à Co. Nous avons dû pour cela amener M en P (fig.16); nous avons effectué une translation MN vers la droite et NP vers le haut; l’origine O_i a subi la même translation par rapport à O_o. Nous mesurons donc sur les axes du graphe de Co l’abscisse de O_i égale à -a_.J_réac et l’ordonnée de O_i égale à l.J_réac.

Nous en déduisons a et l.

Méthode de Jarret

Nous n’avons besoin dans cette méthode que des deux points M et M’ de Ci.

Le point M’ correspond à V = 0 donc à un essai en court-circuit pour l’intensité J_cc= J_réac. Ce point correspond à la valeur du courant d’excitation I_ecc qui peut être lu sur la caractéristique en court-circuit utilisée dans le modèle linéaire pour déterminer la réactance synchrone.

Au point M’ le triangle de Potier est représenté par M’N’P’; la caractéristique Co étant linéaire près de l’origine, elle est confondue avec le segment OP’. Le point M est connu mais le triangle MNP est inconnu; construisons un triangle MQP égal au triangle M’OP’; pour cela nous portons horizontalement MQ = M’O = I_ecc . Traçons la droite D passant par Q et parallèle à OP’, c’est à dire à la partie non saturée de Co; cette droite coupe Co en P. Les triangles OP’M’ et QPM sont égaux; si nous traçons les hauteurs P’N’ et PN elles sont égales; N est donc le troisième point du triangle de Potier.

En résumé pour cette méthode:

v tracés : dans des axes I_e, E_v nous traçons Co; nous plaçons le point M = (I_eréac,V) . Nous lisons sur Ccc le courant I_ecc correspondant à J_cc = J_réac et nous portons sur une horizontale passant par M et vers la gauche MQ égal à I_ecc à l’échelle des abscisses; par Q nous traçons D parallèle à la partie linéaire de Co ; cette droite coupe Co en P. Nous projetons P orthogonalement en N sur QM.

v calculs : à l’échelle des abscisses NM représente a.;J_réac d’où nous tirons le nombre a ; à l’échelle des ordonnées NP représente l.J_réac d’où nous tirons l en ohms.

La méthode de Potier pour le calcul des coefficients a et l montre que les graphes à vide et en réactif ne peuvent se superposer exactement par translation; ceci veut dire que les coefficients de Potier ne sont pas exactement constants; dans la composition des flux, nous avons considéré les flux j_c et j_fs indépendants et le circuit de fuites non saturable; ceci n’est vrai que si la machine n’est pas très saturée; en saturation forte le trajet commun aux flux dans les dents et sous les dents correspond à un matériau saturé et la réluctance n’est plus négligeable devant celle de l’air. En forte saturation la méthode de Potier est critiquable mais donne des résultats convenables