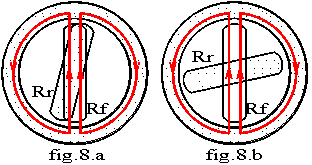
La machine est supposée non saturée.
On peut donc ajouter les flux créés par les divers bobinage
Le flux dans une phase du stator est composé :
v du flux je créé par le courant inducteur Ie, induit dans une phase du stator la f.é.m ev .
v du flux js créé par le rotor fictif dans une phase de l’induit est dû aux trois phases du stator.
Ce flux, dans la phase 1 est la somme : js1 = j11 + j12 + j13 = L1.j1+M12.j2+M13.j3;
L1 est l’inductance propre de la phase 1,
M12 et M13 sont les inductances mutuelles de la phase 1 avec respectivement les phases 2 et 3.
La géométrie du bobinage est telle que M12 = M13 = M ;
js1 = L1.j1+ M.(j2 + j3 ). En régime équilibré j1 +j2 + j3 = 0 d'où js1 = (L1 - M) .j1.
Le flux créé par l’induit dans une de ces phases est donc proportionnel à l’intensité du courant dans cette phase;
nous appelons Ls = L1 - M inductance cyclique ou synchrone d’une phase stator. Tout se passe donc comme si l’inducteur avait l’inductance propre Ls correspondant à la f.é.m. complexe - j.Ls.w.J = - j.Xs.J, en appelant Xs = Ls.w la réactance cyclique ou synchrone.
Les f.é.m. créées par l’induit et l’inducteur s’ajoutent en tenant compte de leurs phases pour donner la f.é.m en charge ech.
Nous pouvons alors donner le modèle dit linéaire ou de Behn-Eschenburg d’une phase stator,en utilisant la convention générateur.
Modèle en convention alternateur
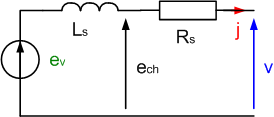
Générateur
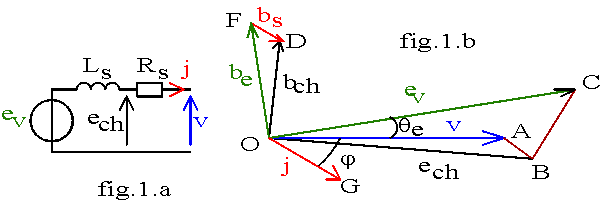
Ech = V + Rs.J et Ev = Ech +j.Xs.J
Moteur
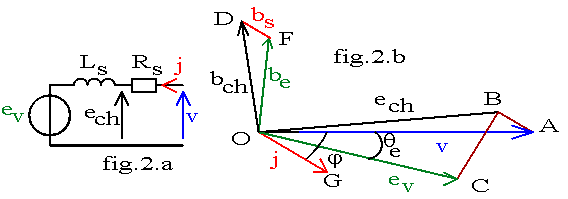
Ech = V - Rs.J et Ev = Ech -j.Xs.J
Essais à réaliser
èMesurer la résistance du stator Rs
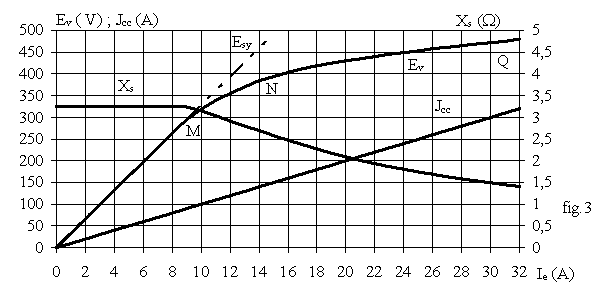
èRelever la caractéristique à vide Ev(Iex)
essai en alternateur à vide à vitesse nominale ns
èRelever la caractéristique de court-circuit Icc (Iex)
essai en alternateur en court-circuit à vitesse nominale ns
En court-circuit, v = 0 donc Ev = Zs.Icc
Pour un même Iex on lit sur la caractéristique Ev et sur la caractéristique en court-circuit le courant Icc ; on en déduit Jcc dans une phase
Zs = Ev(Iex)/Jcc(Iex) et Xs = Ö(Zs²-Rs²)
On peut essayer d'améliorer la méthode :