Électrotechnique
xxModule 5 : xx "Machine synchrone " |
Chapitre 5.1
Principes |
Une machine synchrone est une machine tournante réalisant de façon réversible la conversion d'énergie
mécanique en énergie électrique alternative.
La génératrice synchrone ou alternateur réalise la conversion d'énergie mécanique en énergie électrique.
Le moteur synchrone réalise la conversion inverse.
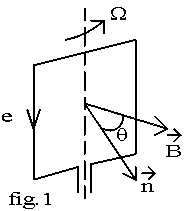
Le principe de la conversion est décrit par la fig.1: une spire rectangulaire verticale, de surface S, tourne autour d'un axe vertical à vitesse W. Cette spire est placée dans un champ magnétique uniforme horizontal B. Soit n le vecteur normal à la spire.
Le flux à travers la spires est :
; nous avons q = W .t + a d'où : j = B.S.cos(W.t + a). Ce flux variable crée une f.é.m induite, comptée positivement dans le sens de la flèche :
e = - dj / dt = B.S.W.sin(W.t + a). Cette f.é.m est sinusoïdale de fréquence f = W/2.p .
Nous avons schématisé le principe de l'alternateur.
Imposons dans la spire un courant sinusoïdal d'intensité : i = I.Ö2.cos w'.t. Le moment magnétique de la spire est : M = S.i . Le champ B crée un couple de moment :
T = B.S.i.sin q = B.I.S.Ö2.cos(w'.t) .sin(W.t + a ).
En utilisant cosp.sinq = [sin(q+p)+sin(q-p)]/2, il vient :
T = Tmax.[ sin (W t + a + w' ) + sin (W t + a - w' )] avec Tmax = B.I.S.Ö2/2. Ce moment est la somme de deux fonctions sinusoïdales de pulsations W+ w' et W- w' ; ces fonctions alternatives ont une valeur moyenne nulle sauf si W = w' ; dans ce cas T = Tmax.[sin(2.W .t + a) + sin(a )]; la valeur moyenne du couple est alors égale à Tmax. sin a
Nous avons schématisé le fonctionnement en moteur.
La machine ne peut fournir un couple que si la vitesse est égale à la pulsation du courant; cette vitesse unique permettant le fonctionnement moteur est dite vitesse de synchronisme. Pour toute vitesse différente, le système a un couple moyen nul, en particulier au démarrage où W = 0 .
2 Constitution de la machine synchrone
Pour réaliser une machine suivant le principe décrit ci-dessus, il faut créer un champ tournant par rapport au bobinage.
Nous pouvons envisager deux solutions:
v un bobinage tournant donc placé au rotor et un inducteur fixe, donc placé au stator, créant un
champ constant
v un bobinage fixe donc placé au stator et un inducteur placé au rotor créant un champ tournant.
Le rotor doit être connecté à la plaque à bornes de la machine par un système de contacts mobiles: des balais fixes glissent sur des bagues cylindriques solidaires du rotor. La transmission de courants d'intensité élevée par ce type de contact induit des pertes importantes; pour les machines de forte puissance, il vaut mieux réserver ce contact au bobinage travaillant sous la puissance la plus faible, c'est à dire à l'inducteur
Une machine synchrone comportera donc:
Ø un rotor servant d'inducteur; cet inducteur doit créer un champ tournant, il sera alimenté en courant continu et comportera 2.p pôles. Le rotor pourra être à pôles lisses ou à pôles saillants. Pour les machines de faible puissance on pourra utiliser un rotor formé d'aimants permanents. Ce type de rotor évite l'utilisation de bagues et de balais puisqu'il n'y a pas à créer de courant inducteur.
Ø un stator servant d'induit. Ce stator comporte un bobinage à q phases (généralement q =1 ou q =3) et doit avoir le même nombre de pôles que le rotor.
3.1 F.é.m induite dans un conducteur de l'induit
Répartition sinusoïdale du champ
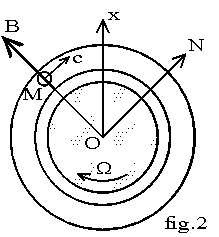
Soit Ox l'axe fixe du stator et ON l'axe d'un pôle Nord du rotor. En admettant que ces axes sont confondus en t = 0, nous avons (Ox , ON) = W.t . Soit un conducteur placé au stator au point M défini par (Ox,OM) = qo = Cste. Le champ magnétique créé en M par le rotor est radial et son amplitude varie en fonction du temps.
Suivant le calcul du chapitre 6,module 1, nous avons : b(qo, t)= Bm.cos[p.(W.t - qo)].
Soit c la vitesse de glissement du champ tournant : c = ri.W en appelant ri le rayon de l'induit.
La f.é.m eb créée dans le conducteur ou barre de longueur L est
eb = b.L.c = ri.W.L.Bm.cos [p.(W .t- qo )].
De cette formule nous déduisons plusieurs propriétés de la f.é.m. :
v la pulsation de eb est w = p.W; sa fréquence est donc f = p.W/2.p; W/2.p est la fréquence de rotation
du rotor en tours par secondes. Soit n la fréquence de rotation exprimée plus couramment en tr/min,
il vient f = p.n / 60.
Pour une fréquence f = 50Hz nous aurons les fréquences de rotation:
type de machine nombre de pôles p vitesse (tr/min) machine bipolaire machine quadrupolaire machine hexapolaire machine octopolaire machine décapolaire machine dodecapolaire v la phase de la f.é.m. est égale à -p.qo; elle ne dépend que de la position du conducteur par rapport à l'axe Ox;
si nous prenions un autre conducteur, placé en M', avec (Ox,OM') = qo+ a, la phase de la f.é.m e'b induite dans ce conducteur serait -p.qo-p.a et donc cette f.é.m. serait déphasée de -p.a par rapport à eb
v la valeur efficace de la f.é.m. est: Eb = ri.W.L.Bm / Ö2 = L.ri.(2.p.f /p).Bm / Ö2.
Pour augmenter cette f.é.m efficace, en gardant la fréquence constante, on peut:
augmenter la longueur de l'induit L; cette longueur est limitée par la flèche du rotor de même longueur augmenter le rayon ri de l'induit, donc du rotor pour garder un entrefer faible; ce rayon est limité par la force centrifuge s'exerçant sur les pièces et les bobinages du rotor; cette limite est plus faible pour les rotors à pôles saillants que pour les rotors à pôles lisses.
diminuer le nombre de pôles 2.p, il faut alors augmenter proportionnellement la fréquence de rotation donc réduire le rayon de l'induit.
augmenter le champ magnétique Bm; la valeur maximale de Bm est limitée à 1,5 T environ par la saturation du circuit magnétique.
Nous rencontrerons deux types de machines:
Ø les machines "rapides" (n = 3000 ou 1500 tr/min) ayant donc peu de pôles (2 ou 4); le rotor est à pôles lisses, de diamètre réduit, de grande longueur; ces machines sont utilisées dans les centrales électriques thermiques.
Exemple: alternateur triphasé de 250 MW ; 3 000 tr/min ; 12,6 kV ; 14300 A; rotor bipolaire de 112 tonnes en acier, comportant 28 encoches pour le bobinage; stator de 252 t.
Ø les machines "lentes" ayant de 6 à 14 pôles ; le rotor est le plus souvent à pôles saillants, de grand diamètre et de faible longueur. Ces machines sont utilisées dans les centrales hydroélectriques.
Exemple: alternateur triphasé 42,5 MW ; 600 tr / min; 10 kV ; 245 A; rotor à 10 pôles saillants alimenté sous 120 V; 750 A.
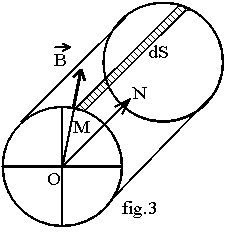
Donnons une autre expression de la f.é.m eb: calculons le flux F à travers la surface d'un pôle; prenons par exemple un pôle Nord de la machine à quatre pôles représentée fig.3;
soit ON l'axe du pôle; pour une machine à 2.p pôles, chaque pôle couvre un pas polaire d'angle
a = p / p; les points M appartenant à la surface d'un pôle sont tels que : -p /2.p £ q p /2.p . Au point M le champ radial a pour module b = Bm.cos p.q . Prenons la surface élémentaire dS découpée par un secteur angulaire dq. La longueur de l'arc est ri.dq et la surface dS = L.ri.dq d'où le flux à travers dS : dj = b.dS = L.ri.Bm. cos (p.q).dq .
Pour avoir le flux sous un pôle nous intégrons entre les limites angulaires du pôle N :
Dans la formule de la valeur efficace Eb remplaçons L.ri.Bm par p.F/2, il vient:
Eb = p.W.F /2.Ö2 ; p.W est la pulsation w= 2.p.f de la f.é.m.; il vient donc: Eb=(p /Ö2).f.F = 2,22.f.F .
Cette formule sera employée par la suite bien qu'elle masque les paramètres géométriques de la machine.
La f.é.m créée dans une barre a une fréquence proportionnelle à la vitesse de rotation n en tr / min
f = p.n / 60 ; sa valeur efficace est proportionnelle au flux sous un pôle. Deux barres décalées
mécaniquement de a ont des f.é.m déphasées de p.a .
Répartition non sinusoïdale du champ
Le champ magnétique b a pour décomposition en série de Fourier:
b(t, q) = B1m.cos[p(W.t-q)]+B3m.cos[3.p.(W.t-q)]+...+Bkm.cos[k.p.(W.t-q)]+..., k étant un nombre impair.
La f.é.m. dans un conducteur devient: eb = L.ri.W.b(t,qo) soit
eb =L.ri.W.[B1m.cos[p(W.t-q)]+B3m.cos[3.p.(W.t-q)]+...+Bkm.cos[k.p.(W.t-q)]+...].
Le terme ebk= L.ri.W.Bkm.cos[k.p.(W.t-qo)] est de pulsation k.p.W = k.w; c'est donc l'harmonique de rang k de la série de Fourier de la f.é.m. eb. Les harmoniques de la répartition spatiale du champ magnétique créent les harmoniques de la f.é.m. Si nous voulons produire une f.é.m. sinusoïdale il faut annuler les harmoniques de la répartition spatiale du champ.
La f.é.m efficace est Eb = L.ri.W.Beff avec Beff = Ö[(B1m²+B3m²+B5m²+...+Bkm²+...) /2] calculée à partir de la série de Fourier. Notons que la phase de la f.é.m ebk est -k.p.qo ; deux barres décalées mécaniquement d'un angle a auront des harmoniques k de la f.é.m. déphasés de -k.p.a.
3.2 Facteur de distribution
Répartition sinusoïdale du champ
Le bobinage d'induit de l'alternateur est formé de faisceaux de conducteurs placés dans les encoches
de l'induit réparties régulièrement. Deux encoches consécutives sont décalées mécaniquement de l'angle a. Les f.é.m des conducteurs dans ces deux encoches sont donc déphasées de p.a; il faut tenir compte de ce déphasage pour ajouter les f.é.m de deux conducteurs placés dans des encoches différentes et mis en série dans le bobinage.
Prenons une machine à 2.p pôles, q phases, Ne encoches régulièrement réparties, comportant N' conducteurs par encoches. Nous avons donc au total Nt =N'.Ne conducteurs d'induit et N=N'.Ne / q conducteurs attribués à chacune des phases. L'écart angulaire entre deux encoches est a = 2.p / Ne. Il y a z = Ne/(2.p.q) encoches par pôle et par phase. Pour un conducteur placé en q = qo nous avons
eb= ri.W.L.Bm.cos[p.(W.t- qo)] = Ebm.cos(w.t-p.qo).
Les N' conducteurs d'une même encoche sont connectés en série dans une même phase; les f.é.m. de ces conducteurs sont en phase donc ils contribuent à la f.é.m totale de la phase pour la quantitée
enc= N'.eb = Eencm.cos(w.t-p.qo) avec Eencm=N'.Ebm.
Les conducteurs des z encoches d'un même pôle et d'une même phase sont mis en série; pour calculer
la f.é.m. ep créée par ces conducteurs, il faut ajouter les z f.é.m. d'encoches en tenant compte de leurs
déphasages. Supposons la première encoche placée en qo= 0, il vient:
f.é.m encoche 1 en q = 0 : eenc1= Eencm.cos(w.t)
f.é.m encoche 2 en q = a : eenc2 = Eencm.cos(w.t-p.a)
f.é.m encoche 3 en q =2.a : eenc3 = Eencm.cos(w.t-2.p.a)
.........................................................................………………………….
f.é.m encoche z en q = (z -1).a : eencz= Eencm.cos[w.t+(z -1).p.a].
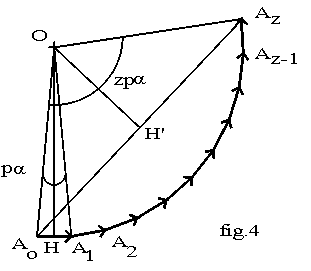
Faisons la somme par la méthode de Fresnel ( fig.4).
AoA1 représente eenc1 , A1A2 représente eenc2 , avec AoA1= A1A2 et (AoA1, A1A2 ) = p.a ... ainsi de suite jusqu'à Az-1Az représentant eencz.
La f.é.m par pôle ep est représentée par la somme AoAz . Les z f.é.m. régulièrement déphasées forment une partie de polygone inscrit dans un cercle de centre O.
Le triangle OAoA1 est isocèle en O. Projetons O orthogonalement en H sur AoA1 ; la hauteur OH est aussi la médiatrice et la bissectrice.
L'angle au centre (OAo,OA1)= p.a; donc l'angle (OAo,OH) = p.a/2. Dans le triangle rectangle OAzH, nous avons : OAz = AzH /sin(p.a/2)= AoA1 / 2.sin(p.a/2)
Le triangle OAoAz est isocèle, d'angle au sommet z.p.a . Soit OH' sa hauteur, il vient
AoH'=AoAz /2.sin(z.p.a/2) soit A0H'= OAo.sin(z.p.a/2).
Nous obtenons finalement: AoAz /AoA1 = sin(z.p.a/ 2) / sin(p.a/ 2).
Les normes des vecteurs de Fresnel étant proportionnelles aux valeurs efficaces des grandeurs représentées, il vient: Ep / Eenc= sin(z.p.a/2) / sin(p.a/2). Si tous les conducteurs étaient dans la même encoche la f.é.m serait z.Eenc; la distribution des conducteurs dans les encoches successives donne un résultat différent.
Nous appelons facteur de distribution le nombre Kd = Ep / z.Eenc; pour un alternateur ayant par pôle et
par phase z encoches régulièrement décalées de a, ce facteur est égal à:
Kd= sin(z.p.a/ 2) / z.sin(p.a/ 2).
Nous obtenons donc pour les conducteurs d'un pôle et d'une phase la f.é.m efficace :
Ep= z.Kd.Eenc= z.Kd.N'.Eb.
Si le bobinage est à pas diamétral, c'est à dire si chaque conducteur d'un pôle Nord est mis en série avec le conducteur du pôle Sud consécutif décalé d'un pas polaire a, les bobinages des 2.p pôles sont identiques. La f.é.m efficace E créée par tous les conducteurs d'une phase est
E = 2.p.Ep= 2.p.z.Kd.N'.Eb. z étant le nombre d'encoches par pôle et par phase, 2.p.z représente le nombre total d'encoches attribué à chaque phase Ne / q; 2.p.z.N' = N représente le nombre de conducteurs par phase. Il vient donc: E = Kd.N.Eb; en remplaçant Eb par sa valeur en fonction du flux par pôle, nous obtenons l'expression de la f.é.m pour une phase :
Une machine synchrone à 2.p pôles à répartition de champ sinusoïdale dans laquelle le rotor crée le flux F par pôle, possédant N conducteurs par phase, a une f.é.m. sinusoïdale de fréquence f et de valeur efficace E = 2,22.Kd.N.f F
Répartition non sinusoïdale du champ
Nous avons vu que dans chaque barre on avait une f.é.m. composée d'harmoniques impairs ebk.
Calculons la valeur efficace Ek de l'harmonique k de la f.é.m. par phase en additionnant d'abord les f.é.m créées par les conducteurs d'un pôle puis celles créées par les 2.p pôles.
La différence par rapport au calcul précédent provient du déphasage électrique k.p.a des f.é.m. de deux encoches successives au lieu de p.a. Le facteur de distribution Kdk de l'harmonique k s'obtient donc par : Kdk = sin(k.z.p.a /2)/ z.sin(k.p.a/2).
Nous obtenons donc: Ek = 2.p.z.Kdk.Epk = 2.p.z.N'.Kdk.Ebk =N.Kdk.Ebk avec Ebk = L.ri.W. Bkm/Ö2.
La f.é.m efficace E par phase s'obtient donc par:
E = Ö(E1²+E3²+...+Ek²+...) = (N.L.ri.W /Ö2).Ö (Kd1².B1m²+Kd3².B3m²+...+Kdk².Bkm²+...).
Exemple 1
Soit un alternateur monophasé à 2.p = 2 pôles créant un champ à répartition spatiale sinusoïdale;
cet alternateur a Ne = 48 encoches régulièrement réparties; soit N'= 4 le nombre de conducteurs par encoche et F =18 mWb le flux par pôle.
Calculons le facteur de distribution lorsque toutes les encoches sont utilisées:
z =Ne /2.p.q=48 /2 /1 = 24 encoches par pôle ;
a=2.p / Ne= p / 24.Kd=sin(24.p / 24 /2)/ 24.sin(p/24/2) = sin(p/2) /24.sin(p /48) = 0,637.
La f.é.m de cet alternateur est: E =2,22.Kd.N.f.F; avec N= 4*48= 192 et f = 50Hz, nous obtenons:
E = 261V.
Supposons maintenant que l'on ne bobine que 2/3 des encoches. Nous avons Ne = 32; z =16 ; a ne change pas car on a toujours le même nombre total d'encoches;
Kd = sin(16.p /48) /16.sin(p / 48) = 0,828. Le nombre de conducteurs est 4*32 = 128 d'où la f.é.m
E = 212 V.Cet exemple montre l'importance du facteur de bobinage: en ne bobinant que 2/3 des encoches donc en économisant 33% de cuivre, on ne diminue la f.é.m que de 19 %. Les encoches les plus éloignées de l'axe d'un pôle à un instant donné ne contribuent que faiblement à la f.é.m totale. L'alternateur monophasé utilise mal le circuit magnétique.
Exemple 2
Soit un alternateur triphasé (q = 3) à 2.p = 12 pôles comportant Ne =108 encoches toutes bobinées et N' =10 conducteurs par encoche. Cet alternateur travaille à f = 50 Hz avec un champ à répartition sinusoïdale créant un flux par pôle F = 50 mWb.
Nous avons z = Ne /2.p.q = 3 ; a = 2.p/108 = p/54 ; p = 6 ; N=Ne.N' /q = 360; p.a/2=p /18.
Le facteur de bobinage est: Kd = sin(3.p/18)/3.sin(p /18) = 0,96.
Cette valeur nous montre qu'en attribuant un tiers de pôle à chacune des trois phases nous utilisons beaucoup mieux le circuit magnétique qu'en monophasé.
La f.é.m par phase est E=2,22 * 0,96 * 360 * 50 * 0,05 = 1 918 V.
Exemple 3
Soit un alternateur triphasé comportant 2.p = 6 pôles; l'induit est de longueur L = 31 cm et de rayon
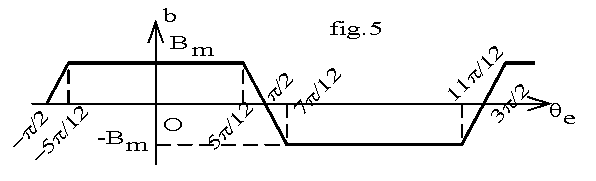
ri = 22 cm; le bobinage comporte Ne = 72 encoches régulièrement réparties et N' = 2 conducteurs par encoche. La machine fonctionne à la fréquence f =50 Hz. La répartition spatiale de champ est représentée sur la fig.5 en fonction de l'angle électrique qe = p. q sur la fig.5.
Le flux sous un pôle est F = 50 mWb.
Calculons l'induction maximale en fonction du flux par pôle:
L'intégrale de b est égale à l'aire du trapèze représentant le champ sous un pôle; cette aire est égale à la demie somme des bases multipliée par la hauteur, soit : (5.p / 6 + p ).Bm/ 2; il vient
F = 11.p.ri.L.Bm /12.p nous en déduisons Bm = 0,764 T.
Décomposons B(qe) en série de Fourier; la fonction étant paire et alternative le développement ne contient que des termes en cosinus de rang impair; l'harmonique de rang k impair a la valeur:
bk(qe) = Bk.cos k.qe avec Bk = -(48.Bm /p².k²) cos(7.k.p /12).
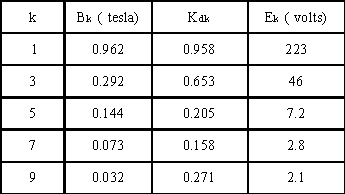
Pour chaque harmonique, nous calculons Bk , le facteur de bobinage Kdk avec p = 6, a = p / 36 et
z =4, la f.é.m. efficace Ek = N.ri.L.W.Kdk.Bmk / Ö2 avec N = Ne.N' /q et W = w/p = 100.p / 3.
La f.é.m. efficace est E = 228,2 V. Le fondamental E1 représente 98 % de la f.é.m totale.
La diminution du coefficient de distribution lorsque k augmente réduit les harmoniques de la f.é.m par rapport à ceux du champ magnétique.
3.3 Facteur de bobinage
Nous avons calculé la f.é.m par phase en supposant le bobinage à pas diamétral et les encoches parallèles à l'axe de la machine; ce n'est pas toujours le cas; la modification du bobinage amène à remplacer le coefficient de distribution par un coefficient de bobinage prenant en compte tous les paramètres.
facteur de raccourcissement
Dans un bobinage à pas diamétral, chaque conducteur est mis en série avec un conducteur décalé d'un pas polaire a = p /p; on a sauté pour cela n encoches et progressé de l'angle n.a = n.p /p; ceci n'est possible que si le nombre d'encoches est Ne = 2.p.n, multiple du nombre de pôles; si ce n'est pas le cas, les spires du bobinage devront couvrir moins d'un pas polaire, nous dirons qu'elles sont raccourcies.
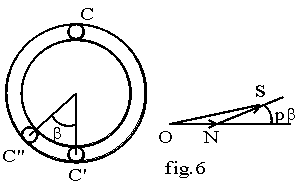
Sur la fig..6, pour une machine bipolaire, nous relions le conducteur C du pôle Nord au conducteur C' du pôle Sud pour faire une spire à pas diamétral; pour raccourcir le pas, nous relions C à C" décalé mécaniquement de b par rapport à C'. Les f.é.m. créées par l'ensemble des conducteurs d'un pôle ePN pour le pôle Nord et ePS pour le pôle Sud sont déphasées de l'angle électrique p.b. La f.é.m de la machine est la somme de ces f.é.m de même valeur efficace Ep. Sur la fig.6, nous avons dans le triangle ONS:
E² =EPN² + EPS² + 2.EPN.EPS.cosp.b = 2.Ep².(1 +cosp.b) = 4.Ep².cos2.(p.b /2) .
Lorsque le bobinage n'est pas raccourci, nous avons E = 2.Ep.
Le raccourcissement introduit un facteur de raccourcissement Kr = |cos (p.b / 2)| < 1.
Le raccourcissement diminue la f.é.m de la machine donc semble uniquement nuisible au bon fonctionnement.
Ce procédé est utilisé pour étouffer les harmoniques de la f.é.m; pour l'harmonique k, le déphasage électrique est p.k.b donc le facteur de raccourcissement est Krk = cos(k.p.b /2); si nous choisissons b tel que k.p.b / 2 = p / 2, Krk = 0 et l'harmonique Ek de la f.é.m s'annule.
Reprenons l'exemple 3; pour étouffer l'harmonique 5, il faut 5.p.b / 2 = p / 2 soit b = p / 15.
Cet angle doit être multiple du décalage d'encoche a = p /36.
Prenons b = p /18. Avec cette valeur les coefficients de raccourcissement valent:
Kr1 = 0,966 , Kr3 = 0,707 , Kr5 = 0,259 , Kr7 = 0,259 , Kr9 = 0,707 .
Nous perdons donc 3,4 % sur la f.é.m. fondamentale, 29,3% sur les harmoniques 3 et 9, 74,1% sur les harmoniques 5 et 7.
Nous avons donc réduit sensiblement le taux d'harmoniques.
facteur d'inclinaison
Lorsque le rotor est à pôles lisses la largeur de l'entrefer est légèrement modulée par l'alternance des dents et des encoches du rotor défilant devant un point fixe. La réluctance de l'entrefer est donc modulée ainsi que le champ magnétique. Si le rotor a Ner encoches et tourne à la vitesse angulaire W, la pulsation de la modulation est Ner.W =Ner.p.w et sa fréquence f ' = Ner.p.f , avec f fréquence des grandeurs statoriques. Cette modulation introduit des harmoniques de fréquences k'.f ' donc de rang k'.p.Ner dans la f.é.m; ces harmoniques sont dits de denture.
Par exemple avec un rotor bipolaire à 28 encoches fonctionnant à 50 Hz, les harmoniques de denture auront les fréquences 1 400 Hz, 2 800 Hz, 4 200Hz...
Pour réduire ces harmoniques, nous inclinons les encoches par rapport à l'axe de la machine en leur donnant une forme d'hélice. Dans ce cas les éléments successifs d'une même encoche sont décalés dans l'espace donc créent de f.é.m. déphasées.
La f.é.m par barre n'est plus L.c.b(q), il faut intégrer les f.é.m. élémentaires des segments sur la longueur d'une barre.
Si les deux extrémités de la barre sont décalées mécaniquement de g, on montre qu'il faut multiplier la f.é.m de l'harmonique k de la machine par le facteur d'inclinaison Kik = sin(p.k.g /2 ) / (p.k.g /2 ) .
Si nous prenons g =2.p/Ner , (p.k.g /2 ) = p.k.p/Ner .
Pour les harmoniques de denture k = k'.p.Ner et sin(p.k.g /2 ) =sin(p.2.k'p ) = 0.
Ce choix d'inclinaison élimine les harmoniques de denture.
Dans l'exemple 3, avec Ner = 28 et p =3, il vient (p.g /2 ) =3.p / 28; le facteur d'inclinaison du fondamental est Ki1 = 0,981 provoquant une perte de 2 % sur la f.é.m.
Le facteur de bobinage K de la machine est le produit des trois facteurs de distribution, de raccourcissement et d'inclinaison: K = Kb.Kr.Ki .
Pour une machine nous avons une f.é.m à vide: E = 2,22.K.N.f.F .
La fréquence est liée à la vitesse par n = 60.f /p, d'où E = 2,22.K.N.(p.n /60 ).F; la f.é.m. d'une machine synchrone est comme celle d'une machine continue proportionnelle à la vitesse et au flux:
E = k.n.F. Pour une machine excitée par un courant continu Ie et fonctionnant à vitesse n = Cste, la f.é.m est liée au courant inducteur par la caractéristique réluctive. La caractéristique E(Ie) à n =Cste est la caractéristique à vide de la machine synchrone.
Cette caractéristique à vide à la même allure que celle de la machine continue; à Ie = 0 la f.é.m. est égale à la f.é.m. rémanente; lorsque Ie augmente le graphe est d'abord linéaire tant que le circuit magnétique n'est pas saturé; ensuite le graphe s'incurve dans le coude de saturation et la f.é.m. varie très peu avec Ie.
Cette caractéristique est relevée en faisant fonctionner la machine en alternateur à vitesse constante et à vide