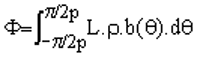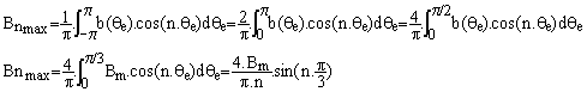Électrotechnique
x x Module 5: x
"Machine synchrone" |
Chapitre 5.1
Principes
|
Calcul de la f.é.m. pour un champ à répartition sinusoïdale
On étudie une machine synchrone triphasée dont le stator est couplé en étoile. Le stator comporte Ne = 54 encoches régulièrement réparties et 12 conducteurs par encoche. L'induit est de longueur L = 30 cm et de rayon r = 20 cm |
|||
1.1 La vitesse étant n = 1000 tr/min, la fréquence de la f.é.m. est f = 50 Hz. Combien la machine possède-t-elle de pôles ? |
ns = 60.f/p donc p = 3 paires et 2.p = 6 pôles |
||
1.2 Calculer le coefficient de distribution Kd |
Kd= sin(z.p.a/ 2) / z.sin(p.a/ 2) z = Ne/2.p/3 = 3 encoches par pôle et par phase a = 2.p/Ne = p/27 Kd = 0,96 |
||
1.3 Le flux par pôle est F = 40 mWb. Calculer la f.é.m. d'une phase |
E=2,22.Kd.N.f.F N = 54*12 = 648 conducteurs E = 2 762 V |
||
1.4 Calculer la tension en ligne dans un fonctionnement en alternateur à vide |
Couplage étoile donc U = E.Ö3 = 4 784 V |
||
2.1 Quelle doit être la valeur du champ maximal Bm pour que le flux par pôle soit F = 40 mWb ? |
Intégrer en utilisant le changement de variable qe = p.q |
Bm = 0,955 T |
|
2.2 Montrer que la décomposition en série de Fourier de b(qe) n'a que des termes en cosinus de rang impair |
b est une fonction paire donc il n'y a que des termes en cosinus b est une fonction alternative donc, il n'y a que des termes de rang impair
|
||
2.3 Calculer la valeur maximale de l'harmonique n de b(qe) |
|
||
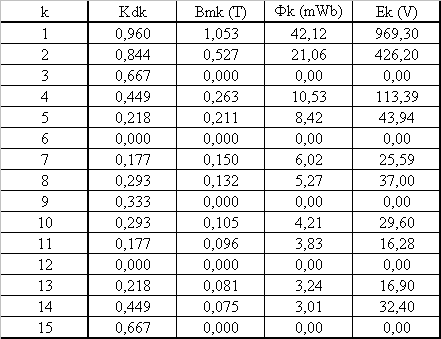
2.4 Pour les harmoniques de rang 1 à 15, calculer le facteur de distribution et la f.é.m. efficace |
Kdk = sin(k.z.p.a /2)/ z.sin(k.p.a/2) Fk = 2.L.r.Bmk/p Ek = 2,22.Kdk.N.f.Fk |
N = nombre de conducteurs par phase = 54*12/3 = 216 nombre de paires de pôles p = 3 décalage des encoches : a = 360/54 = 6,67 ° z = nombre d'encoches par pôle et phase = 54/6/3 = 3
|
|
2.5 Calculer la valeur efficace de la f.é.m. |
E = ÖS(Ek²) = 1 068 V |
||
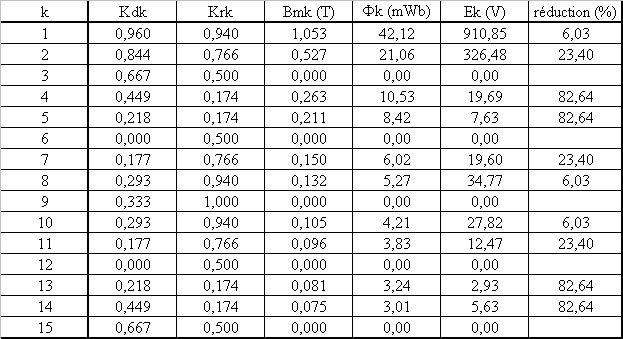
2.6 On crée un raccourcissement de deux encoches, reprendre les questions 2.4 et 2.5 |
On crée un raccourcissement b = 2.a = 2.p/27 |
E = 969 V |
|
2.7 Quel est l'intérêt du raccourcissement ? |
On atténue les harmoniques en affaiblissant peu le fondamental (voir tableau de la question précédente) |
||
