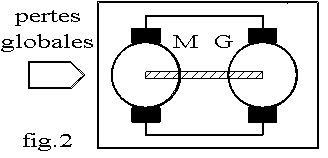Les bases de Windows XP

Dans le chapitre 3.1 du module, nous avons étudié les pertes de la machine continue. Ces pertes peuvent être classées en trois groupes:

Ø les pertes calculables : ces pertes peuvent être calculées à partir des données du point de fonctionnement; ce sont les pertes par effet Joule dans l’induit et dans l’inducteur.

Ø les pertes mesurables : ces pertes peuvent être mesurés à partir d’essais indirects, c’est à dire sans essai sur charge réelle. Ces pertes dites «constantes» sont les pertes mécaniques et les pertes dans le fer.

Ø les pertes supplémentaires : ces pertes n’apparaissent qu’en charge et ne peuvent être déterminées que par un essai direct en charge.

1.2 Rendement

Le rendement vrai de la machine est : h = Puissance utile / Puissance absorbée.

v Pour un fonctionnement moteur, la puissance utile est la puissance mécanique sur l’arbre P_u = T_u.W et la puissance absorbée est la puissance électrique fournie à l’induit augmentée de la puissance fournie à l’inducteur si l’excitation est séparée.

v Pour un fonctionnement générateur, la puissance utile est la puissance électrique fournie par l’induit

P_u= U.I et la puissance absorbée est la puissance mécanique T_m.W augmentée de la puissance électrique fournie à l’inducteur si l’excitation est séparée.

Ce rendement ne peut être mesuré que par un essai direct en charge.

Le rendement approché est le rendement calculé en ne prenant en compte que les pertes calculables et mesurables. La puissance électrique absorbée en moteur ou fournie en générateur est calculée; la puissance mécanique s’en déduit par soustraction en moteur ou addition en générateur des pertes calculables et mesurables. Ce rendement est calculé à partir des pertes obtenues dans des essais indirects.

2 Mesure du rendement vrai

Il nous faut réaliser un essai en charge et mesurer:

· tension et courant d’induit

· tension et courant inducteur si l’excitation est séparée

· vitesse et moment du couple utile.

La mesure la plus difficile à réaliser est celle du couple. Le plus souvent cette mesure est faite en utilisant une machine balance comme charge du moteur ou comme entraînement du générateur. Cette machine est une machine continue en excitation séparée dont les paliers sont montés sur roulements pour permettre au stator de tourner autour de son axe. Par réaction, le couple sur l’arbre tend à entraîner le stator; ce couple est alors équilibré par une masse m coulissant sur un bras de levier fixé perpendiculairement à l’axe de rotation. La masse du bras est équilibrée par un contrepoids; la masse m étant placée à distance D de l’axe, le couple sur l’arbre est : T = m.g..D avec g = 9,81 m.s^-2.

La mesure du rendement vrai est rarement utilisée car:

v elle nécessite un essai en charge coûteux en énergie avec un dispositif onéreux de mesure de couple.

v le rendement est calculé à partir de quatre mesures U, I, T, n et donc sa valeur est entachée d’une erreur importante. Si chaque mesure est faite avec une erreur relative de 2%, le rendement est connu à 8% près; si nous mesurons pour un moteur h = 90%, le rendement sera compris entre 82,8% et 97,2%. Pour une puissance utile P_u = 1 000 kW, la puissance utile sera comprise entre 1 029 kW et 1 208 kW soit une incertitude de 179 kW sur la puissance consommée, quantité non négligeable.

3 Méthode des pertes séparées

Il s’agit de calculer un rendement approché à partir d’essais indirects permettant de connaître les pertes mesurables et calculables.

Soit un point de fonctionnement A caractérisé par un type de fonctionnement moteur (M) ou générateur (G) avec les grandeurs d’induit U(A), I(A), d’inducteur I_ex(A) et par une vitesse de rotation n(A).

3.1 Pertes calculables

Ø Les pertes par effet Joule dans l’inducteur sont calculées à partir du courant dans l’inducteur I_ex (A) et de la résistance de l’inducteur R_ex. La résistance de l’inducteur est mesurée par une méthode volt-ampèremétrique appropriée à l’ordre de grandeur de la résistance. Dans le cas d’une excitation séparée, nous devons y ajouter les pertes dans les organes de réglage du flux inducteur.

Ø Les pertes par effet Joule dans l’induit sont calculées par p_ja = R.I_a^²(A). Cette formule est entachée d’erreur car la résistance d’induit n’est pas constante. La résistance de contact entre les balais et le collecteur varie en fonction du courant d’induit; en particulier elle est beaucoup plus grande aux faibles intensités. Pour tenir compte de ce phénomène, nous pouvons utiliser la résistance R mesurée par une méthode volt-ampèremétrique courte dérivation avec un courant d’induit supérieur à la moitié du courant nominal; dans ce cas la résistance est sous estimée aux faibles intensités mais les pertes par effet Joule sont alors faibles et l’erreur commise est peu conséquente.

Ces mesures doivent être faites «à chaud» c’est à dire à la température nominale de fonctionnement q_f de l’ordre de 75 à 85°C. Si cela est possible nous faisons fonctionner la machine pendant environ un quart d’heure à son point nominal avant la mesure. Si cela n’est pas possible, nous faisons la mesure à la température ambiante q_a et nous appliquons la formule de correction: R(q_f ) = [1 + 0,0042.(q_f - q_a). ].R(q_a )

3.2 Pertes mesurables

Les pertes dites constantes sont mesurées en faisant fonctionner la machine en moteur à vide excité par une source séparée, quels que soient son mode de fonctionnement (M ou G) au point A et son mode d’excitation (séparée, dérivation, série).

Dans cet essai au point Av les pertes constantes doivent être aussi semblables que possible aux pertes réelles pour le point A étudié:

v les pertes mécaniques ne sont fonction que de la vitesse: l’essai à vide se fera à la vitesse n(Av) = n(A).

v les pertes dans le fer sont fonction du flux et de la vitesse; la vitesse étant la même, le flux dans l’essai à vide doit être égal au flux en charge; à vitesse constante, le flux est proportionnel à la f.é.m.; la f.é.m. de l’essai à vide doit être égale à celle du point A. En moteur à vide, la f.é.m. est :E(Av) = U_v - R.I_v . A vide nous aurons U_v très peu différente de E(Av).

Au point A, la f.é.m. est E(A) = U ± R.I(A) , + pour un fonctionnement au point A en générateur, - en moteur.

L’essai sera conduit de la façon suivante:

è régler le courant d’excitation maximal et démarrer le moteur

è régler la tension d’induit U_v à la valeur E(A)

è régler le courant d’excitation pour avoir n(Av) = n(A); avec le même flux, nous devons avoir I_ex(Av) égal à I_ex(A) si nous négligeons la réaction d’induit.

è mesurer le courant d’induit I_v.

Dans cet essai à vide la puissance électromagnétique est égale aux pertes constantes; il vient :

p_c = p_mec + p_fer =P_emv = E(Av).I_v = (U_v - R.I_v ).I_v .

3.3 Calcul du rendement

Au point A nous connaissons les pertes et la puissance électrique absorbée par l’induit: P_elec = U(A).I(A).

Ø En moteur nous calculons:

· la puissance absorbée P_a = P_elec + kp_jex avec k = 0 en excitation dérivation ou série et k = 1 en excitation séparée.

· la puissance utile P_u = P_a - (p_mec + p_fer +p_ja+k.p_jex).

v En générateur nous calculons:

· la puissance utile P_u = P_elec

· la puissance absorbée P_a = P_u + (p_mec + p_fer +p_ja+p_jex).

3.4 Séparation complète des pertes

Si nous désirons étudier plus finement les pertes constantes p_c nous pouvons séparer les pertes mécaniques et les pertes dans le fer.

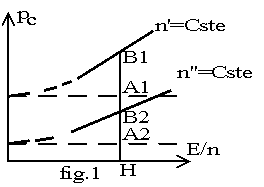
Pour cela nous faisons l’essai à vide à tension U_v variable et à vitesse n_v constante; dans cet essai les pertes mécaniques sont constantes; les pertes dans le fer sont proportionnelles au carré du flux donc à vitesse constante au carré de la f.é.m E_v peu différente de U_v. Si nous traçons le graphe p_c (U_v^²) nous obtenons une droite. Si nous extrapolons le graphe jusqu'à U_v = 0, nous avons p_c(U_v = 0) = p_mec(n_v).

Nous pouvons ainsi séparer les pertes mécaniques et les pertes dans le fer.

Si nous voulons séparer encore plus finement les pertes, c'est à dire mesurer les pertes par frottements

p_mf = a.n, les pertes par ventilation p_mv = a'.n^², les pertes par hystérésis p_fh = c.n.F^² et les pertes parcourants de Foucault p_cf = c'.n^².F^² , il suffit de faire l'essai décrit ci-dessus pour deux vitesses n' et n". Pour avoir une même échelle de flux, nous traçons les graphes de p_c en fonction du flux donc de E / n. En extrapolant les graphes à E = 0, nous obtenons les pertes mécaniques : p_mec( n') = HA₁ et p_mec( n") = HA₂ .

Pour un flux donné correspondant à OH sur l’axe des abscisses, nous avons:

(1) HA₁ = p_mec(n') = a.n' + a’.n' ^² ;

(2) HA₂ = p (n") = a.n"+ a’.n"^² ;

(3) A₁B₁ = p_fer(n',F) = c.n'.F² +c’.n' ^².F^² et A₂B₂ = p_fer(n",F) = c.n".F^² +c’.n"^².F^² .

Des équations (1) et (2) nous tirons les coefficients a et a’ ; des équations (3) et (4), nous tirons les coefficients c et c’ .

Cette séparation complète des pertes n’est guère effectuée que lors de la conception d’une machine continue pour comparer les diverses pertes et voir s’il est possible de modifier la machine pour réduire les pertes les plus importantes.

3.5 Critique de la méthode

Cette méthode a l’avantage de la simplicité; elle ne nécessite que la machine étudiée et deux sources de tension de puissance faible devant la puissance nominale de la machine.

Son inconvénient est de donner un rendement approché; nous ne tenons pas compte des pertes supplémentaires et les pertes sont mesurées dans l’essai à vide donc dans des conditions différentes de la marche en charge. En particulier nous avons égalé le flux en charge créé par l’induit et l’inducteur avec le flux dans l’essai à vide créé par le seul inducteur. La répartition des lignes de champ n’est pas la même dans les deux cas donc les pertes dans le fer peuvent être différentes.

4 Méthodes de récupération

4.1 Principe

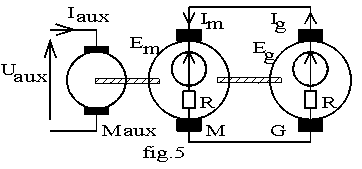
Pour éliminer la critique faite à la méthode des pertes séparées, nous mesurons les pertes dans un essai en charge. Pour rendre l’essai possible et moins coûteux, nous ne dissipons pas la puissance utile dans un récepteur mais nous la récupérons en utilisant le montage de la fig.2.

Deux machines identiques sont couplées mécaniquement et électriquement. Les deux machines sont généralement utilisées en excitation séparées de sens tels que les f.é.m soient en opposition. Une machine fonctionne en moteur (M) et l’autre en générateur (G); aux pertes près, chaque machine fournit à l’autre sa puissance absorbée. Il suffit donc de fournir au groupe l’ensemble de ses pertes pour entretenir le fonctionnement.

Les pertes globales du groupe peuvent être fournies :

v mécaniquement en accouplant un moteur auxiliaire sur l'arbre du groupe

v électriquement par une source en série ou en parallèle avec les induits.

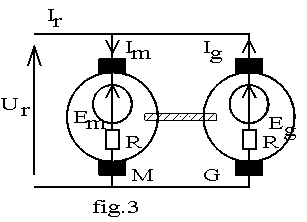
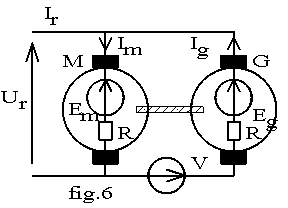
v en combinant deux des éléments précédents.

4.2 Méthode de Rayleigh-Kapp

Dans cette méthode, les pertes sont fournies par une source de tension U_r connectée en parallèle sur les induits. Nous avons : p_mot + p_gen = U_r.I_r soit p_mot + p_gen = U_r.(I_m -I_g).

Nous avons I_m > I_g donc les pertes par effet Joule sont plus grande dans M que dans G. U_r =E_m +R.I_m = E_g -R.I_g ; la f.é.m. du générateur est supérieure à celle du moteur; il en est de même pour les flux donc

p_ferG > p_ferM; les deux machines ayant la même vitesse ont les mêmes pertes mécaniques . Les pertes des deux machines sont différentes et il est difficile de répartir les pertes globales entre M et G. Nous devons faire une hypothèse de calcul:

Pour I < Inom / 2

les chutes ohmiques de tension sont faibles devant les f.é.m et les pertes par effet Joule sont faibles devant les autres pertes; les f.é.m des deux machines sont sensiblement égales donc nous supposons l’égalité des pertes: p_M = p_G =U_r.I_r / 2.

POUR I > Inom/2

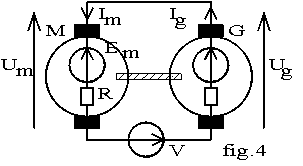
les pertes des deux machines sont différentes; dans cette zone de fonctionnement le rendement d’une machine est quasi indépendant du courant d’induit; nous supposons donc l’égalité des rendements d'induit : h_aM = P_mec/ U_r.I_m et h_aG = U_r.I_g / P_mec d’où h_aM.h_aG = I_g / I_m.

Nous en déduisons h_aM = h_aG = Ö (I_g / I_m). Les pertes d’induit des machines sont :

p_M = U_r .I_m - P_mec = U_r.I_m.(1-h_aM) et p_G = P_mec - U_r.I_g = U_r.I_g (1-h_aG) / h_aG.

Les pertes étant connues, les rendements se calculent comme dans la méthode des pertes séparées.

Cette méthode a l’avantage de nécessiter une seule source d’alimentation mais le calcul des pertes est entaché d’une erreur due à l’hypothèse de calcul.

4.3 Méthode de Potier

Dans cette méthode les pertes sont compensées par une source de tension en série avec les induits.

Nous avons : I_m = I_g = I ; p_M + p_G = V.I ; U_m = V + U_g

Si les courants d'excitation des deux machines sont égaux, nous avons:

E_m = E_g et V = ( E_m + R.I ) - (E_g - R.I) = 2.R.I; nous en déduisons V.I = 2.R.I^² = 2.p_j . Ceci est impossible car les pertes ne sont pas totalement compensées par la source V; les deux machines doivent donc avoir des f.é.m différentes et nous nous retrouvons dans le cas de la méthode précédente. Le calcul des pertes est mené avec les mêmes hypothèses.

4.4 Méthode d’Hopkinson

Les pertes sont fournies par un moteur taré auxiliaire Maux, c'est à dire un moteur dont le rendement h_aux est connu.

Les pertes du groupe sont :

p_M + p_G = h_aux.U_aux.I_aux .

Les courants d'induit des machines sont égaux mais les f.é.m diffèrent de 2.R.I. Les pertes des machines sont donc différentes et le calcul se fait suivant la méthode du paragraphe 4.2.

4.5 Méthode d’Hutchinson

Nous utilisons deux sources électriques pour fournir les pertes : une en parallèle et une en série (fig.6).

Les pertes globales sont : p_M + p_G = U_r.I_r + V.I_g . Si les courants d’excitation des machines sont égaux,

E_m = E_g et V = R.(I_m+I_g); la puissance fournie par la source en série est V.I_G = R.(I_m.I_g+I_g^² ); la source parallèle ne fournissant qu’une partie des pertes, I_r est faible devant I_m donc I_m et I_G sont voisins et la puissance fournie par la source série est quasi égale aux pertes par effet Joule dans les induits des machines. La source parallèle fournit donc les pertes constantes.

Nous avons : (p_mec + p_fer )_m = (p_mec + p_fer)_g = U_r.I_r / 2 , p_jm = R.I_m^² et p_jg = R.I_g^² .

Cette méthode ne nécessite pas d'hypothèse sur la répartition des pertes.

4.6 Critique des méthodes de récupération

Ces méthodes ont l’avantage de mesurer les pertes dans un essai en charge réelle; elles ne sont pas seulement destinées à la mesure du rendement mais permettent aussi de mener des essais en charge pour tracer les graphes caractéristiques des machines.

Ces méthodes ont l’inconvénient de nécessiter deux machines identiques. Les essais sont délicats à mener. De plus le calcul des pertes se fait en utilisant des hypothèses de répartition entre les machines qui ne sont pas toujours exactement vérifiées suivant les méthodes et les points de fonctionnement.

Les méthodes les plus simples à mettre en oeuvre, c’est à dire celles à une seule source d’énergie, ne s’appliquent pas aux machines à aimant permanent car elles supposent de f.é.m différentes pour M et G donc des flux différents.