Électrotechnique
x x Module 3: x
"Machine à courant continu" |
Chapitre 3.3
Fonctionnement
en auto-excitation
|
Une machine à courant continu porte sur sa plaque signalétique : 110 V - 50 A - 1 500 tr/min - excitation dérivation On donne : la résistance de l'induit R = 60 mW et celle de l'inducteur Re = 70 W
la caractéristique à vide CV : Eo(Ie) relevée à vitesse nominale
le moment du couple de pertes est supposé constant en valeur absolue : |Tp| = 2 Nm
|
||
Cliquez ici pour utiliser la caractéristique à vide |
||
Étude du régime permanent en moteur |
||
1. La machine fonctionne en moteur au point nominal |
||
1.1 Calculer le courant d'excitation Ie |
Dans un premier temps, on peut confondre les courants d'alimentation I et d'induit Ia car Ia >> Iex |
E = U-R.Ia » U-R.I = 107 V Lire sur CV : Ie = 0,63 A On a bien Ia >> Iex |
1.2 Calculer la résistance du rhéostat d'excitation
|
Rhe+Re = U /Iex = 175 W donc Rhe = 105 W |
|
1.3 Calculer le moment du couple utile |
Tem = E.I / W = 34 Nm Tu = Tem - Tp = 32 Nm |
|
1.4 Calculer le rendement |
Pu = Tu.W = 5027 W Pa = U.I = 5 500 W h = Pu /Pa = 91,5 % |
|
2 La machine fonctionne en moteur; le rhéostat d'excitation garde la valeur calculée au 1.2.et le moment du couple utile garde la valeur du 1.3. La tension d'induit est réglée à U = 55 V |
||
2.1 Calculer le courant d'induit |
Montrer que Tem est inchangé. Calculer la nouvelle valeur du courant d'excitation et en déduire la constante de flux à partir de Cv |
Tu = 32 Nm ; Tem = Tu+Tp = 34 Nm Ie = U/(Rhe+Re)= 55/175 = 0,315 A Sur Cv Eo = 57 V donc k.F = Eo/Wo =0,363 Vs Ia= Tem / k.F = 93, 7 A
|
2.2 Calculer la vitesse |
E = U - R.Ia = 49,4 V n = no.E/Eo = 1300 tr/min |
|
2.3 Comparer ce résultat à celui que l'on obtiendrait en excitation séparée |
En excitation séparée, le flux est constant donc à couple constant Ia est constant E = U-R.Ia = 52 V n = no.E/Eo = 1500*52/107 = 730 tr/min La vitesse serait quasiment divisée par 2 comme U alors qu'elle ne diminue que de 13% en excitation dérivation |
|
2.4 Calculer le rendement |
I = Ia + Ie = 94 A Pu = Tu.W = 4356 W Pa = U.I = 5 170 W h = Pu /Pa = 84,3 % |
|
Réversibilité régime permanent Le rhéostat d'excitation est en court-circuit. Le couple résistant est constant : Tr = 15 Nm. On néglige le courant inducteur Ie devant le courant d'induit Ia |
||
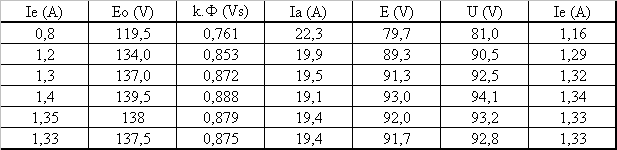
3.1Calculer la tension et le courant d'induit pour une vitesse n = 1000 tr/min |
On peut calculer le couple électromagnétique Tem = k.F.Ia mais on ne connaît ni Ie donc pas le flux ni Ia On va procéder par essais successifs : se donner une valeur de Ie, en déduire k.F, Ia, E, U et donc Ie; faire des essais jusqu'à ce que Ie calculé corresponde à Ie choisi au départ |
Tu = Tr ; Tem = Tu+Tp = 17 Nm Si Ie = 1 A, on lit sur Cv, Eo = 128 V à no donc k.F = Eo/Wo = 0,815 Ia = Tem/ k.F= 20,9 A ; E = Eo.n/no = 85,3 V ; U = E+RI = 86,6 V ; Ie = 1,24 A, valeur différente de 1 donc on recommence avec une autre valeur
On retient U = 93 V et Ia = 19,4 A |
Pour arrêter la machine on veut imposer un couple constant Tu = -5 Nm |
||
4.1 Comment doit-on faire en pratique ? |
La constante de temps de l'inducteur et la constante de temps électromécanique sont grandes devant la constante de temps électrique de l'induit; donc, si on diminue U, n et Iex ne changent pas instantanément et E reste constante. Si U < E , Ia < 0 donc Tu < 0 |
|
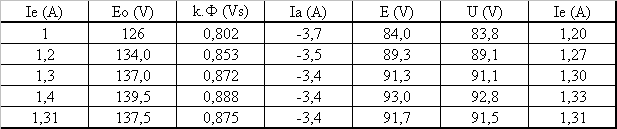
4.2 La vitesse restant égale à n = 1000 tr/min, calculer la valeur de U. |
Utiliser la même méthode que pour la question 3.1 |
Tu = -5 Nm; Tem = Tu+Tp = -3 Nm
|
La vitesse étant de n = 500 tr /min, on veut passer à n = -500 tr/min |
||
5.1 Décrire le mode opératoire |
Pour avoir une vitesse négative, il faut inverser la tension ou le flux; si on inverse U, Ie s'inverse donc le flux devient négatif et la vitesse reste positive. Il faut donc inverser les connexions de l'inducteur . On ne peut ouvrir l'inducteur sous tension, il faut donc diminuer la tension jusqu'à 0, inverser le connexions puis augmenter progressivement la tension. |
|
5.2 Calculer la tension pour le régime permanent n = -500 tr/min |
Tu = 15 Nm; Tem = Tu+Tp = 13 Nm car n < 0 implique Tp < 0
|
|
|
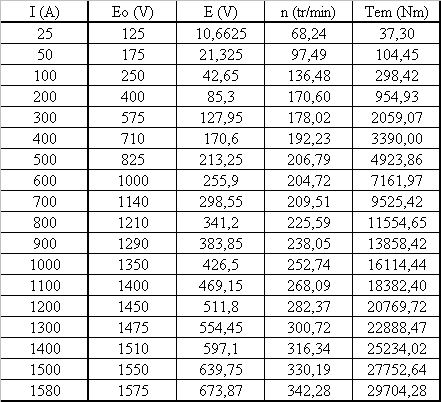
v la caractéristique à vide Eo(I) relevée à no = 800 tr/min
v la caractéristique du rendement en fonction du courant d'induit, pour une tension d'alimentation U = 1500 V v les résistances de l'induit R = 19 mW et de l'inducteur Rs = 7,5 mW |
||
Cliquez ici pour utiliser les caractéristiques |
||
Étude du régime permanent en moteur Le moteur est alimenté sous U=1 500 V et l'intensité d'induit est I =1 500 A |
||
1.1 Calculer la fréquence n de rotation, les moments Tu du couple utile, Tem du couple électromagnétique et Tp du couple de pertes. |
I = 1500 A ; Eo = 1550 V à no ; E = U-(R+Rs).I = 1460 V à n n = no.E/Eo = 754 tr/min Pa = U.I = 2250 kW ; h = 95 % Pu = h.Pa = 2 138 W ; Tu = Pu / W = 27 kNm Tem = E.I / W = 27,74 Nm ; Tp = Tem - Tu = 740 Nm |
|
1.2 Même question si on branche une résistance Rs = 48 mW en parallèle sur l'inducteur. |
Ks = Rh/(Rh+Rs) = 0,865 Is = Ks.I = 1297 A ; Eo(Is) = 1475 V à no E = U-(R+Ks.Rs).I = 1462 V à n n = no.E/Eo = 793 tr/min Pa = U.I = 2250 kW ; h = 95 % Pu = h.Pa = 2 138 W ; Tu = Pu / W = 25,8 kNm Tem = E.I / W = 26,4 kNm ; Tp = Tem - Tu = 610 Nm |
|
2 Étude du démarrage : le courant au démarrage est limité à 2400 A |
||
2.1 Calculer le moment du couple au démarrage sans rhéostat d'excitation |
I = 2400 A ; Eo = 1820 V à no k.F = Eo / Wo= 21,72 Vs Tem = k.F.I = 52,1 kNm ; Tp = 0 à l'arrêt donc Tdem = 52,1 kNm |
|
2.2 Calculer la tension à appliquer |
E = 0 donc U = (R+Rs).I = 63,6 V |
|
Freinage en génératrice On dispose d'une résistance de freinage Rf = 400 mW pouvant dissiper 1MW. On néglige le couple de pertes. |
||
3 Freinage en génératrice série |
||
3.1 La vitesse étant positive, dans quel quadrant du plan n(T) doit-on faire fonctionner la machine |
n > 0 et Tu < 0 donc quadrant 2 |
|
3.2 Expliquer pourquoi le freinage en récupération, c'est à dire en renvoyant l'énergie au réseau, ne peut être utilisé avec une génératrice série |
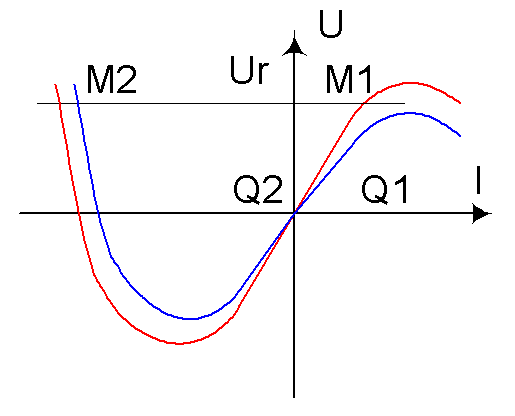
En convention générateur U = E - R'.I; la caractéristique en charge est représentée ci-dessous, en rouge pour une vitesse n1 et en belu pour une vitesse n2 < n1
Le réseau étant de tension Ur, à vitesse n1, la machine fonctionne en génératrice au point M1; si la vitesse baisse, il n'y a plus de fonctionnement dans le quadrant 1 Le point de fonctionnement passe en M2; I a changé de signe donc le flux change de signe; le courant étant négatif, le couple est positif et la vitesse négative; la machine change donc brutalement de sens de rotation |
|
3.3 Décrire le mode opératoire |
Pour passer de Q1 à Q2, il faut inverser le couple mais pas la vitesse;si on branche la machine sur la résistance, le courant s'inverse donc le flux aussi, le couple ne change pas de signe et la vitesse s'inverse et on fonctionne dans Q3. Il faut donc inverser les connexions de l'inducteur. |
|
3.4 Déterminer la vitesse maximale à la quelle on peut utiliser la résistance de freinage. Calculer le moment du couple de freinage |
Si on garde les conventions moteurs U = E+(R+Rs.I) = -Rf.I avec E > 0 et I < 0 E = -Rt.I avec Rt = R+Rs+Rf = 426 mW. Pf = Rf.I² donc Imax = -1580 A Umax =-Rf.I = 632 V et Emax = 673 V Pour I = 1580 A on a Eo = 1580 V à no = 800 tr/min On a donc nmax = no.Emax / Eo = 340 tr/min Tem = Tu = E.I/W = -29,9 kNm |
|
3.5 La résistance de charge étant fixée, quelle est la vitesse minimale permettant l'amorçage de la génératrice série ? Quelle est alors la valeur du moment du couple de freinage ? |
L'amorçage est possible si la droite E = Rt.I a une pente inférieure à la pente de la caractéristique à vide dans sa partie linéaire. Cette pente est a = (720-400)/(400-200) = 1,6 W à no Cette pente est proportionnelle à la vitesse. La vitesse nmin à laquelle cette pente devient a' = Rt est nmin = no.a'/a = 213 tr/min Le courant d'induit ainsi que le couple sont quasi nuls |
|
3.6 Entre ces deux vitesses limites, exprimer le moment du couple en fonction de la vitesse. |
Si on se donne une valeur de I, on en déduit sur Cv la f.é.m. Eo à no et on calcule E à la vitesse n en écrivant que U = Rf.I = E -(R+Rs).I soit E = (R+Rs+Rf).I et n = no.E/Eo
|
|
3.7 Que peut-on conclure de cette étude ? |
La plage de vitesses permettant le freinage est très réduite. Le freinage sera très brutal et le couple décroît rapidement avec la vitesse
|
|
4 Freinage en génératrice excitation séparée : l'inducteur est alimenté par une batterie avec un courant d'excitation Is = 450 A. |
||
4.1 Exprimer le moment du couple de freinage en fonction de la vitesse |
Is = 450 A donne Eo = 800 V à no soit une constante de flux K = E/Wo = 9,55 Vs Tem = Tu = K.I ; E = K.W = -Rt.I donc I = -K.W/Rt et Tu = -K².W/Rt = --214.W = -22,4.n |
|
4.2 Quelles sont les limites de vitesse permettant le freinage ? |
Imax = -1580 A donc Emax = -Rt.Imax = 674 V nmax = no.Emax/Eo = 800*674/800 = 674 tr/min Imin = 0 donc nmin = 0 |
|
4.3 Conclure |
En excitation séparée, la plage de vitesses permettant le freinage est beaucoup plus grande avec un couple proportionnel à la vitesse De plus un réglage séparé du courant d'inducteur permet d'ajuster la plage de vitesses et/ou le couple de freinage |
|