Électrotechnique
x x Module 3: x "Machine à courant continu" |
Chapitre 3.2
Fonctionnement
en excitation séparée
|
Nous étudions une machine continue excitée soit
èpar des aimants permanents ; le flux inducteur est alors constant
-
èpar des bobinages statoriques alimentés par une source de tension indépendante du circuit d'induit; dans ce cas, le flux inducteur est fonction du courant d'excitation Iex .
Les paramètres intervenant dans le fonctionnement sont
èle flux inducteur Fp lié au courant d'excitation Iex
èla tension U et le courant I d'induit
èla vitesse n et le moment du couple Tu
Ces paramètres sont liés par les équations de la machine.
>2.1 Conventions d'orientation
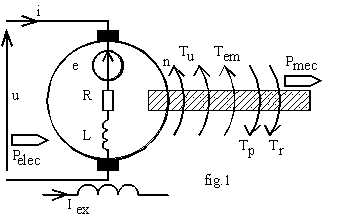
La machine continue étant le plus souvent utilisée en moteur, nous définissons des conventions pour que toutes les grandeurs soient positives lors de ce fonctionnement avec un sens de rotation direct.
L'induit peut être modélisé par la f.é.m. e, la résistance de l'induit R et l'inductance propre de l'induit L. Le courant est orienté en sens inverse de la f.é.m. et la tension en sens inverse de i (convention récepteur).
Le couple moteur est orienté dans le sens de la vitesse (générateur de puissance mécanique) ainsi que le couple électromagnétique. Le couple de pertes est résistant quel que soit le fonctionnement, il est donc orienté en sens inverse de la vitesse; le couple imposé par la charge Tr est résistant dans le fonctionnement moteur donc est orienté en sens inverse de la vitesse.
2.2 Équations de la machine
L'équation électrique de l'induit donne en régime quelconque : (1) u = e + R.i + L.di / dt.
e est la f.é.m. en charge de la machine : (2) e = k.W.Fch(i ,Iex) ou e = k'.n.Fch(i ,Iex) ;
sa f.é.m à vide est : (3) eo = k.W.Fp(Iex) ou eo = k'.n.Fp(Iex) .
Les deux f.é.m. différent de la chute de tension par réaction magnétique d'induit : (4) e(n, i,Iex ) = eo - e
La f.é.m à vide est fonction du courant d'excitation; la relation est décrite par la caractéristique à vide relevée à vitesse constante no , généralement égale à la vitesse nominale nn . A courants d'induit et d'inducteur constants , eo , e et e sont proportionnelles à la vitesse :
(5) eo(n , Iex) /eo(no , Iex) = e(n , i , Iex) /e(no , i , Iex) = e(n , i , Iex) /e(no , i , Iex ) = n / no.
Ces équations vont nous permettre d'établir une liaison entre grandeurs électriques et mécaniques; de (1), (2), (3), (4) et (5) nous tirons:
(6) n = no .(u - R.i) /[eo(no , Iex) - e (no , i , Iex) ]
La puissance électromagnétique est Pem = e(n ,i , Iex).i d'où (7) Tem = k.I.Fch(i , Iex) .
Le couple de pertes est de sens opposé à la vitesse n, son signe change avec celui de n; nous pouvons écrire (8) Tp = | Tp |. n / | n |.
Le bilan des couples donne : (9)Tu = Tem - Tp .
La relation fondamentale de la dynamique donne, avec J = moment d'inertie de l'ensemble des parties tournantes ramené sur l'arbre : (10) J.d W/dt = Tu - Tr .
2.3 Régime permanent
En régime continu permanent, toutes les grandeurs sont constantes ; les équations (1) et (10) sont seules modifiées par annulation des dérivées :
u = e + R.i et Tu = Tr .
3 Caractéristiques statiques de la machine en fonctionnement moteur
3.1 Caractéristique de vitesse
L'équation (6) : n = no.(U - R.I) / [ Eo (no , Iex) - e(no , I , Iex)] nous permet de lier la vitesse aux grandeurs électriques.
Si nous fixons U et Iex, nous obtenons la caractéristique de vitesse n( I )
v Négligeons R et e : nous obtenons n = no.U / Eo(no , Iex ) = U / k'.Fp(Iex); à flux constant la vitesse est proportionnelle à la tension d'induit. A tension constante, la vitesse est inversement proportionnelle au flux donc varie en sens inverse du courant inducteur. Si nous supprimons le courant inducteur, le flux inducteur devient égal au flux rémanent quasi nul donc la vitesse atteint des valeurs dangereuses.
Il ne faut jamais supprimer le courant inducteur d'un moteur continu ayant son induit sous tension
v Tenons compte de R mais négligeons la réaction magnétique d'induit : l'expression de la vitesse devient
n = no.(U - R.I) / Eo( no , Iex). A flux constant, nous obtenons n = (U - RI) / K' avec K' = k'.Fp( Iex ); la caractéristique de vitesse est une fonction affine de pente (-R / K' ) inversement proportionnelle au flux. Cette pente est faible donc la vitesse est quasi indépendante du courant d'induit
v En tenant compte de tous les paramètres, nous obtenons une variation non linéaire de la vitesse ; lorsque I augmente le numérateur et le dénominateur de la fonction n(I) diminuent; aux faibles charges R.I augmente plus vite que e donc la vitesse diminue lorsque I augmente. Aux fortes charges la variation de e devient prépondérante donc la vitesse augmente avec la charge.
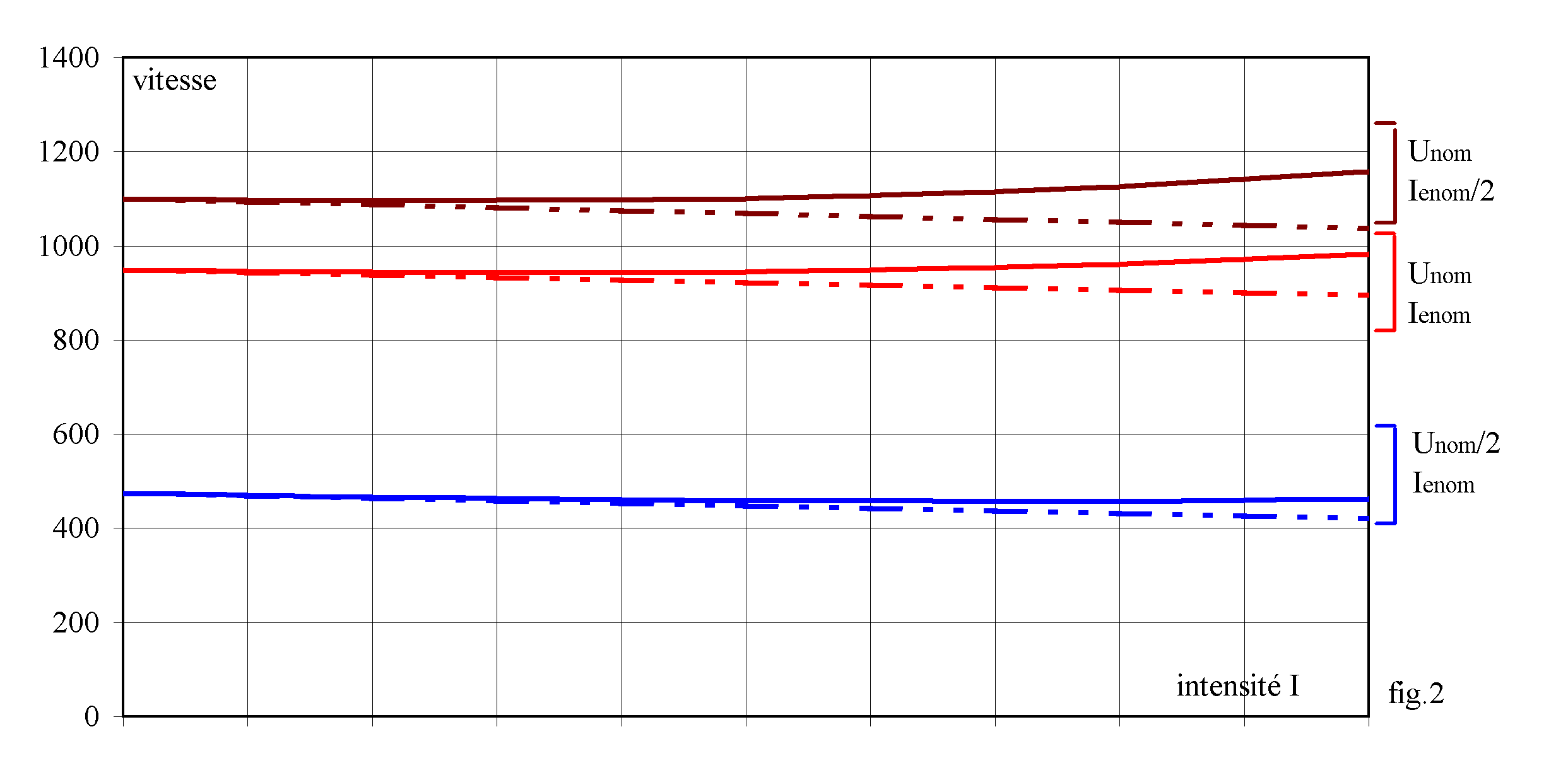
Nous traçons sur la fig.2 l'allure de la caractéristique de vitesse pour plusieurs fonctionnement. Les courbes en trait pointillé représentent les caractéristiques d'une machine compensée ( e = 0).
3.2 Caractéristique électromécanique
Le moment du couple électromagnétique Tem est relié aux grandeurs électriques par :
(7) Tem = k.I.Fch (Iex , I ) . Si nous fixons le courant inducteur, nous pouvons tracer la caractéristique électromécanique Tu ( I ).
v En négligeant la réaction d'induit, le flux en charge est égal au flux à vide donc est constant, il vient :
Tem = K.I , fonction proportionnelle;
v Si l'on tient compte de la réaction d'induit, pour une même valeur de I, le flux donc le moment du couple sont plus faibles.

Les courbes sans repérage correspondent à l'excitation nominale et les courbes avec marques correspondent à un courant d'excitation moitié .
3.3 Caractéristique mécanique
Si nous éliminons l'intensité d'induit entre les deux graphes précédents, nous obtenons la caractéristique mécanique T(n) représentée sur la fig.4:
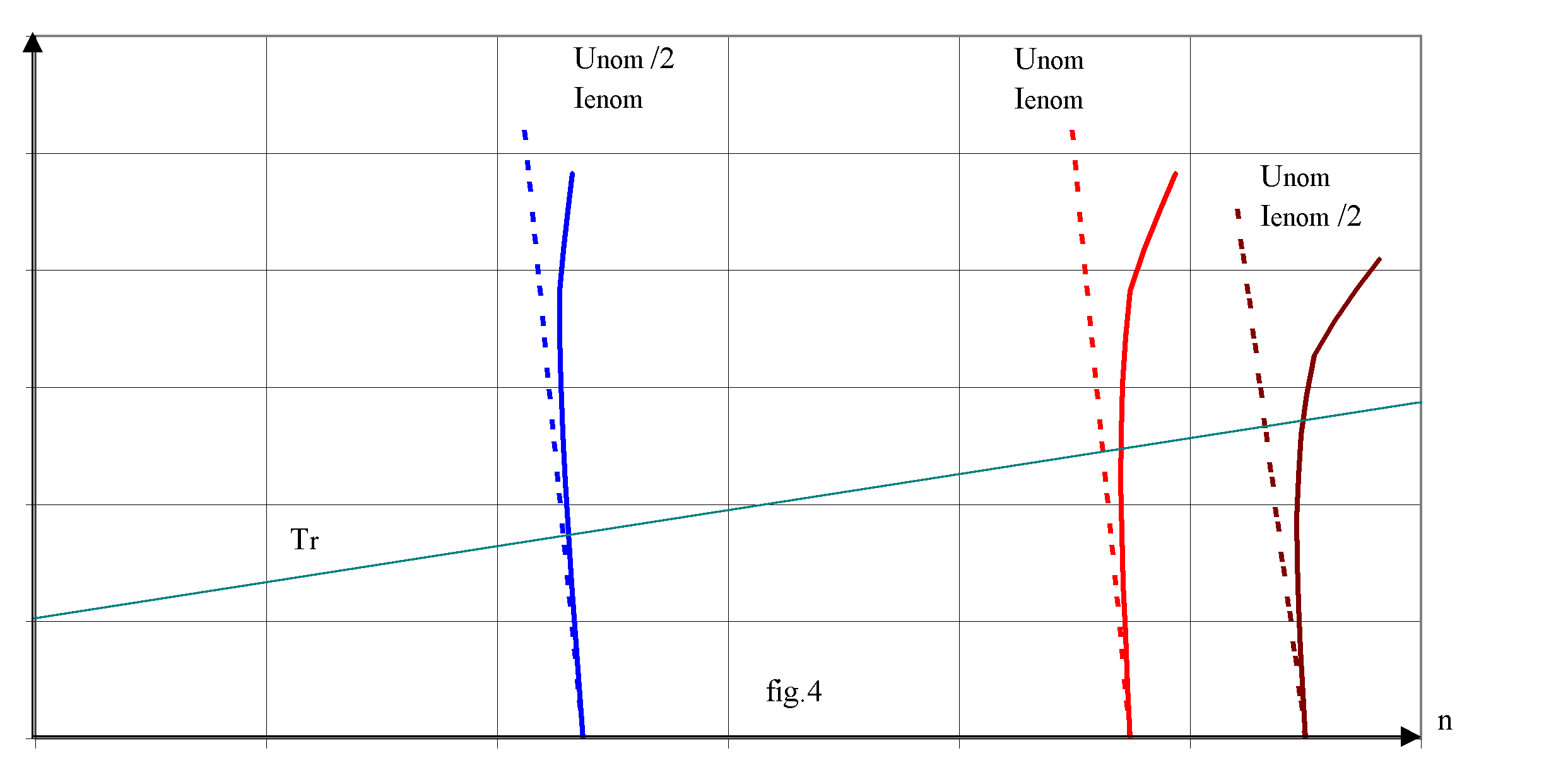
En examinant ce graphe, nous pouvons voir que la vitesse est quasi indépendante du couple.
Lorsque nous voulons régler la vitesse du moteur en maintenant le couple constant, nous pouvons agir sur la tension d'induit ou sur le courant inducteur.
v L'action sur la tension d'induit donne une plage de réglage de 0 à 1,2.nnom environ car la vitesse est quasi proportionnelle à la tension. A flux inducteur constant, le moment du couple est proportionnel à l'intensité; à couple résistant constant, la tension d'induit modifie la vitesse sans modifier le courant d'induit.
v L'action sur l'excitation donne une plage de réglage plus faible en raison de la non linéarité du circuit magnétique; l'augmentation de Iex augmente peu le flux en raison de la saturation donc diminue peu la vitesse (sur la fig.2 : en divisant Iex par 2 la vitesse n'augmente que de 16 %). L'action sur le courant d'excitation se répercute sur le couple; pour un même couple, le courant d'induit augmente si on diminue le courant d'excitation. Nous risquons de ne plus pouvoir fournir un couple suffisant si nous limitons le courant d'induit, par exemple à 1,25 fois sa valeur nominale .
Le réglage de vitesse du moteur continu en excitation séparée se fait principalement par la tension d'induit, le courant inducteur permet des réglages fins. A flux constant le courant d'induit est une image du moment du couple électromagnétique de la machine.
Le graphe ci-dessus montre que la réaction magnétique d'induit peut rendre le fonctionnement instable lorsque le couple augmente avec la vitesse: la machine fonctionne en régime stable avec Tu = Tr , c'est à dire au point d'intersection des graphes de Tu et Tr ; une augmentation de vitesse due à une cause quelconque augmente le couple moteur; celui-ci devenant supérieur au couple résistant, la vitesse augmente encore ; nous avons donc un effet cumulatif; le couple et la vitesse augmentent sans se stabiliser; l'augmentation du couple crée une augmentation du courant d'induit et il va y avoir surcharge électrique faisant disjoncter les protections de l'induit.
4.1 Schéma blocs
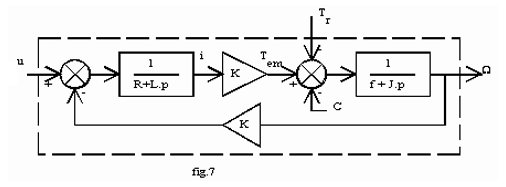
Compte tenu des équations de la machine, on peut modéliser la machine fonctionnant à flux constant suivant la figure 7
4.2 Identification des paramètres
Caractéristiques électriques de l'induit
La mesure avec un ohmmètre ne donne pas de résultat satisfaisant en raison de la faible valeur de cette résistance mais surtout de sa non linéarité à faible courant; lorsque le courant d'induit est faible, la résistance de contact entre les balais est le collecteur est de forte valeur et varie aléatoirement en fonction de l'état du collecteur. Cette résistance diminue dès que le courant atteint 10 à 20 % du courant noiminal.
èL'inductance L de l'induit peut être obtenue à partir de la réponse en courant à un échelon de tension u, rotor bloqué. Comme W = 0, on a : u = R.i + L.di/dt soit i + te.di/dt = u/R. La réponse est une exponentielle; si on mesure le temps Dt mis par le courant pour passer de 10 % de la valeur finale U/R à 90 % de cette valeur te = L / R = Dt /2,2.
Caractéristiques électromécaniques
On réalise un essai à vide du moteur sous tension continue u variable. Le régime permanent étant atteint, on mesure tension, courant et vitesse. On a E = U-R..I= K.W.
En traçant E(W), on calcule la constante de flux K en V.s.
On peut tracer Tem = K.I en fonction de W; comme le couple résistant est nul, Tem = Tp; on peut décomposer le couple de pertes en un couple de frottements secs C indépendant de la vitesse et un couple de frottements fluides f. W ; le tracé de Tp(W) permet de déterminer C = Tp(W=0) et f pente du graphe linéarisé.
Moment d'inertie
Plusieurs méthodes peuvent être utilisées pour déterminer J :
è Démarrage à courant constant : on peut alimenter le moteur à vide par une source continue à limitation de courant et enregistrer courant et vitesse durant le démarrage. Si le courant I = Id = Cste, on a J.dW/dt = K.Id - Tp. Si on considère que la variation de Tp = C+f.w est faible devant K.Id, l'accélération et constante donc la vitesse croît linéairement. Si la vitesse varie de DW = W1 - W2 durant un temps Dt, le couple de pertes moyen est
Tpmoy = [Tp(W1)+Tp(W2)]/2 et J = (K.Id - Tpmoy).Dt /DW .
è Ralentissement libre : on alimente le moteur sous une tension continue U; lorsque la vitesse de régime permanent est atteinte, on ouvre le circuit d'induit. Le courant d'induit s'annule et on a J.dW/dt = - Tp(W). La pente de la tangente à la vitesse Wo est - Tp(Wo) / J; on calcule Tp(Wo) et on en déduit J.
è Démarrage à vide : le moteur étant à vide et à l'arrêt, on applique une échelon de tension Uo.
On enregistre W(t). Si on néglige l'inductance d'induit , Uo = K.W+R.i ; Tem=K.i = K(Uo-K.W)/R ;
J.dW/dt = Tem-Tp-Tr = K.(Uo-K.W)/R- C - f.W ou J.dW/dt + (f+K²/R).W = K.Uo/R - C. La constante de temps électromécanique est tem = R.J/(R.f+K²). La réponse est une exponentielle; si on mesure le temps Dt mis par la vitesse pour passer de 10 % de la valeur finale à 90 % de cette valeur tem = Dt /2,2. On en déduit tem et on calcule J. L'hypothèse L négligeable est validée si te << tem .
5 Principes de commande à flux constant
Si nous négligeons la réaction magnétique d'induit et si nous fixons le flux , k.F(Iex)=K=Cste, les équations sont
(1) u = e + R.i + L.di/dt ; (2) e = K.W = K'.n avec K' = K.p/30
(3) Tem = K.i ; (4) Tp = n.|Tp/ n| (couple toujours résistant)
(5) Tu = Tem - Tp ; (6) J.dW/dt = Tu - Tr (J moment d'inertie des parties tournantes)
On suppose le couple résistant Tr (W ) et le couple de pertes Tp (W ) connus.
Les variables sont : u, i , e, Tem , Tu et W ou n. Avec six variables et cinq équations utilisables ( l'équation 4 ne permet pas le calcul d'une variable), il faut imposer une des variables pour pouvoir calculer les autres. On dit que l'on se fixe une loi de commande. Divers modes sont possibles suivant le choix de la variable.
5.1 Commande en tension
On impose la loi de commande u (t). Dans la majorité des fonctionnements n et u ont le même signe, on connaît donc le signe de Tp à chaque instant.
Les équations (3), (5) et (6) donnent: (7) ![]() ; en utilisant (1) et (2), nous obtenons:
; en utilisant (1) et (2), nous obtenons: ![]() .
.
Nous avons dT(W) /dt = (dT/dW).(dW/dt). Nous en déduisons l'équation de la vitesse :
(8) 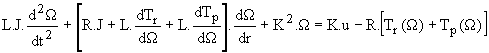
Cette équation permet de calculer la vitesse ; par l'équation (7) nous calculons l'intensité.
La résolution peut être impossible dans le cas où les couples Tp et Tr ne sont pas des fonctions affines de la vitesse. Nous pouvons simplifier la résolution en considérant dans un premier temps que les constantes de temps mécaniques et électriques sont d'ordre de grandeur différents:
v A vitesse nulle, nous avons R.i + L.di/dt = u , la constante de temps électrique est te = L/R. Nous disons que nous sommes en mode électrique.
v Si nous négligeons L, et que nous supposons Tp et Tr constants, l'équation (8) devient :
R.J.dW / dt + K².W = f (t); la constante de temps est tem = R.J / K² . R est un paramètre électrique, J un paramètre mécanique et K = E/W un paramètre mixte; la constante tem est dite électromécanique. Nous dirons que nous sommes en mode électromécanique.
Dans la plus part des cas tem est très grande devant te , nous pouvons considérer que L = 0 pour l'obtention de la vitesse par l'équation (8). Nous dirons alors que les modes électrique et électromécaniques sont découplés.
Ce mode de commande est le plus simple puisqu'il suffit de disposer d'une source de tension continue réglable. Le fonctionnement en boucle ouverte est théoriquement possible.
Le danger de ce mode réside dans le fait de ne pas contrôler le courant. Par exemple, si l'on applique un échelon de tension U au moteur à l'arrêt, nous avons quasi instantanément i =U/R, valeur pouvant être dangereuse électriquement pour la machine et pour la source, et mécaniquement pour les parties tournantes: un couple trop élevé avec une charge de forte inertie peut provoquer une rupture d'accouplement ou d'arbre.
En pratique toute commande en tension doit comporter une boucle de contrôle de courant.
5.2 Commande en vitesse
Nous imposons la loi n(t) ou la loi W(t). L'équation (7) donne la loi de courant i(t) et l'équation (1) la loi de tension u (t). Le calcul est plus simple que pour la commande en tension.
Le mode de commande a les avantages et inconvénients du précédent mais il ne peut fonctionner en boucle ouverte.
5.3 Commande en courant
Nous imposons la loi i(t). L'équation (7) permet alors de calculer la vitesse et l'équation (1) la tension.
Ce mode est complexe à réaliser car on dispose rarement de source de courant pilotée; il faut donc réaliser une boucle de courant pour piloter, à partir de l'erreur entre la consigne i(t) et le courant mesuré, la source de tension alimentant l'induit.
Ce fonctionnement a l'avantage d'écarter les risques électriques puisque le courant est constamment maîtrisé ainsi que les risques de rupture mécanique.
Il peut cependant être dangereux car on ne contrôle plus la vitesse. Avec un courant constant et un couple résistant constant tels que J.dW/dt = Tu - Tr = Cste > 0 la vitesse croît linéairement. Il faudra donc prévoir une limitation en vitesse.
Dans la plus part des cas , la commande comportera une boucle de vitesse et une boucle de courant.
La fig.8 donne l'organisation générale d'une commande en vitesse.
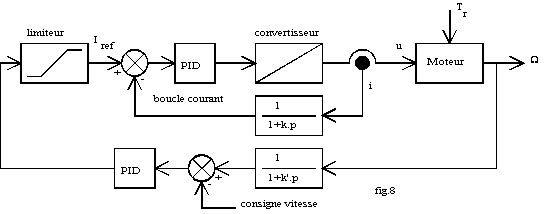
6 Étude du démarrage en moteur
Pour qu'un moteur démarre en partant de l'arrêt, il faut créer un couple moteur supérieur au couple résistant; pour diminuer le temps de démarrage, l'accélération doit être la plus grande possible ; dW/dt =(Tu - Tr )/ J montre qu'il faut créer le couple moteur maximal; pour une vitesse nulle les pertes dans le fer et les pertes mécaniques sont nulles donc Tu = Tem = k.F(Iex).I. Nous devons démarrer avec un courant d'excitation d'intensité maximale et avec un courant d'induit maximal.
Pour n = 0, la f.é.m du moteur est nulle donc U = R.I; le courant de démarrage est réglé par la tension d'induit et la résistance totale du circuit d'induit. Si nous alimentons le moteur sous tension nominale, nous aurons un courant de démarrage allant de 20 à 50 fois le courant nominal. Il faudra donc contrôler ce courant qui risque de détériorer la machine si les protections ne sont pas suffisantes. Pour cela nous pouvons augmenter la résistance du circuit en insérant un rhéostat de démarrage en série ou réduire la tension.
7.1 Principes
Si nous négligeons la résistance d'induit, la réaction magnétique d'induit et le couple de pertes nous avons:
n = nn.U / Eo(nn,Iex) = U / k'.Fp(Iex ) et Tu = Tem = k.I.Fp(Iex ) .
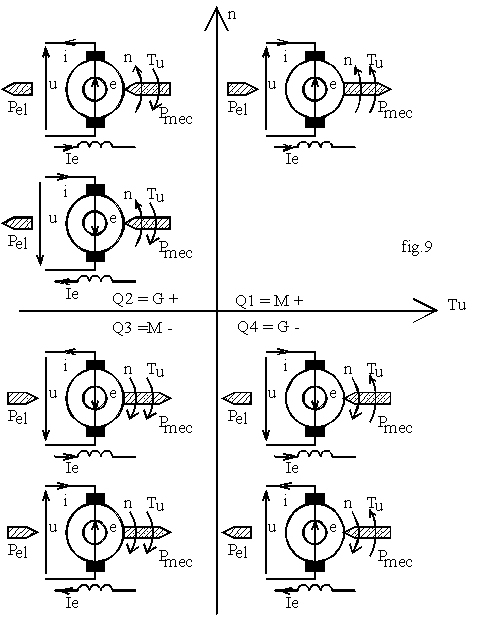
Nous envisageons un fonctionnement quatre quadrants de la machine, ce qui veut dire que dans le plan rapporté aux axes Tu en abscisse et n en ordonnée, le point de fonctionnement peut occuper successivement des positions dans les quatre quadrants du plan. Choisissons les conventions de signe pour les grandeurs de façon à ce qu'elles soient toutes positives dans le quadrant Q1 et que la machine fonctionne alors en moteur. Dans ce quadrant la représentation symbolique est celle de la fig.1.
Si nous voulons passer dans le deuxième quadrant Q2 , Tu devient négatif et n reste positive; la puissance mécanique change de signe et la machine fonctionne en générateur. Pour inverser le couple, il faut inverser une seule des grandeurs I ou Fp(Iex ) c'est à dire Iex ; si nous choisissons l'inversion de I, le signe de n est inchangé et nous ne devons pas modifier U; dans ce premier cas la source électrique ne change pas de polarité.
Si nous choisissons d'inverser le courant d'excitation pour inverser le couple, nous inversons simultanément la vitesse; pour garder n > 0, il faut simultanément inverser la tension U.
Pour passer du quadrant Q1 au quadrant Q3 nous devons inverser la vitesse et le couple; la puissance mécanique reste de même signe donc la machine fonctionne encore en moteur. Pour inverser la vitesse nous pouvons choisir d'inverser U ou Fp(Iex )c'est à dire Iex . Si nous choisissons d'inverser seulement U, le couple n'est pas modifié; pour l'inverser il faut inverser également l'intensité I.
Si nous choisissons d'inverser le courant inducteur pour inverser n, nous inversons simultanément le couple donc le courant I garde le même sens que dans le quadrant Q1.
Pour passer du quadrant Q1 au quadrant Q4, nous devons inverser seulement la vitesse donc U ou Fp(Iex ) c'est à dire Iex . La puissance mécanique change de signe donc la machine fonctionne en générateur. Si nous choisissons l'inversion de U, le couple n'est pas modifié donc il n'est pas nécessaire de modifier le sens de I. Si nous choisissons l'inversion du courant d'excitation, le couple s'inverse; pour garder son signe +, il faut inverser le courant d'induit I.
Les diverses possibilités sont représentées sur la fig.9.
7.2 Réversibilités en fonction de la source d'induit
Les modes à utiliser dépendent de la source disponible pour l'induit. Il est souhaitable d'éviter l'inversion du courant d'excitation; on sait en effet qu'on ne doit jamais annuler l'excitation lorsque l'induit de la machine est alimentée; si nous voulons inverser le courant inducteur, il faut d'abord annuler le courant puis la tension d'induit; il faut ensuite réduire le courant d'excitation pour limiter la surtension due à la forte inductance de l'inducteur, inverser l'alimentation de l'inducteur, rétablir le courant d'excitation puis rétablir les grandeurs d'induit; cette inversion peut prendre plusieurs secondes.
Pour avoir un fonctionnement quatre quadrants sans modifier les alimentations de l'induit et de l'inducteur, il faut disposer d'une source d'induit réversible en tension et en courant.
Si la source d'induit n'est réversible qu'en tension, on peut encore obtenir un fonctionnement quatre quadrants en inversant les bornes de l'induit lorsqu'on doit changer le sens du courant ( passage de Q1 à Q2 ou de Q3 à Q4); pour inverser l'induit, il faudra annuler le courant d'induit en réglant u = e , ouvrir le circuit, inverser les bornes, régler u = - e puis refermer le circuit d'induit; on aura alors i = 0 ; le réglage de u permettra le réglage de la vitesse.