"Machine 
à courant continu"

Chapitre 3.1

Constitution et principes

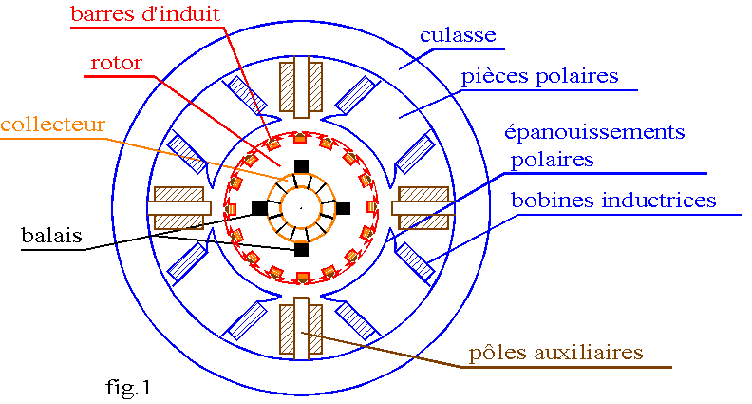
1 description de la machine continue

1.1 Circuit magnétique

èLe stator est l'inducteur de la machine; il réalise une armature fixe hétéropolaire à 2p pôles saillants. Il est formé:

vd'une culasse en acier coulé formant le bâti de la machine; elle est complétée par des pattes de fixation et par deux flasques portant les paliers de l'axe.

vde noyaux polaires en acier doux et massif, portant les bobines inductrices.

vd'épanouissements polaires en acier dur feuilleté; l'ensemble du pôle est vissé sur la culasse.

vde pôles auxiliaires intercalés entre les pôles principaux et portant des bobinages alimentés en série avec l'induit.

Dans les machines de petite puissance, les pôles peuvent être remplacés par des aimants permanents.

Le stator comporte également des porte-balais maintenant des balais en carbone frottant sur le collecteur.

èLe rotor est l'induit; il est formé d'un empilement de tôles en acier; chaque tôle est un cylindre de quelques millimètres d'épaisseur dans lequel sont découpées les encoches destinées à contenir le bobinage d'induit.

èLe collecteur solidaire du rotor est un cylindre formé de lames de cuivre isolées entre elles et placées parallèlement à l'axe.

La fig.2 donne une représentation développée de la machine. Le flux F créé par un pôle ne traverse pas totalement l'entrefer; il existe un flux de fuites caractérisé par le coefficient d'Hopkinson n = F / Fu ; ce coefficient varie de 1,1 à 1,2 suivant les machines. Dans la culasse et dans l'induit, le flux se divise dans deux circuits de même réluctance.

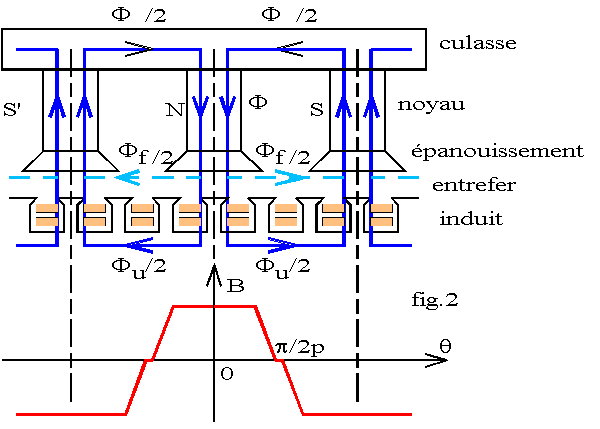
Étudions le circuit magnétique en écrivant le théorème d'Ampère le long d'une ligne de champ traversant un pôle Nord et un pôle Sud : E représente la f.m.m. d'un enroulement polaire: E =Np.Iex , Np est le nombre de spires par pôle et Iex l'intensité du courant inducteur.

Pour un élément du circuit magnétique, R_k représente la réluctance et Rk.Fk = Hk.Lk la d.d.p magnétique. Le théorème d'Ampère donne: 2.E = SHk.Lk ; cette équation permet de tracer la caractéristique magnétique du flux dans l'entrefer Fu = Fp en fonction de l'intensité du courant inducteur.

1.2 Bobinage induit

f.é.m. induite dans une barre

Considérons une barre c'est à dire un conducteur de l'induit situé dans une encoche. L'induit de la machine tourne à la vitesse angulaire W; sa vitesse tangentielle est v = ri.W avec ri rayon de l'induit; l'angle polaire de la barre repéré par rapport à l'axe d'un pôle du stator est q = W.t +qo. De façon approchée, nous pouvons dire que le circuit magnétique focalise les lignes de champ donc que le champ est normal à la barre d'induit ; ceci n'est qu'approximatif car la différence de perméabilité entre la dent et l'encoche déforme les lignes de champ; la f.é.m induite dans le conducteur est e = B.L.v avec L longueur de la barre.

Le champ étant variable avec l'angle polaire q, il vient : e =L.v.B(W.t +qo) = f (t). La f.é.m induite dans une barre est donc variable avec le temps; la fonction f (t) reproduit la répartition spatiale B(q) de l'induction (fig.3 en trait épais); sa pulsation est W pour une machine bipolaire et w = p.W pour une machine multipolaire; cette f.é.m est alternative .

Principe du bobinage

La f.é.m dans une barre étant alternative, nous ne pouvons connecter directement les barres en série pour réaliser le bobinage car la f.é.m de la machine serait alternative alors que nous la voulons continue; le bobinage sera fait en utilisant un collecteur pour recueillir la f.é.m redressée.

Considérons une machine bipolaire ayant deux encoches diamétralement opposées et contenant chacune deux barres (fig.4):

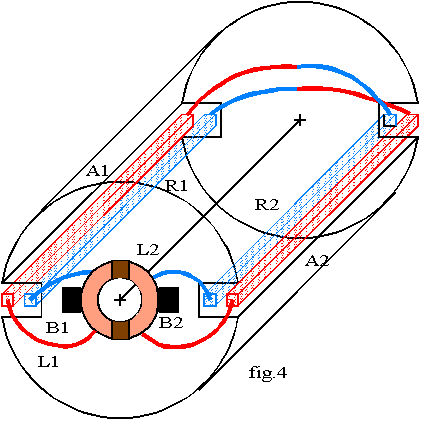
Si les conducteurs A1 et R1 sont situés sous un pôle Nord et ont une f.é.m dirigée de l'avant vers l'arrière, les conducteurs A2 et R2 sont situés sous un pôle Sud et ont donc une f.é.m opposée puisque le décalage des encoches est égal au pas polaire.

Partons du conducteur A1, relions le par la face arrière au conducteur R2 pour former une spire de f.é.m alternative 2e; le conducteur A1 est dit conducteur d'aller et le conducteur R2 est dit conducteur de retour ; nous formons de même une spire de f.é.m 2e avec les conducteurs A2 à l'aller et R1 au retour.

La face avant porte deux demi-cylindres coaxiaux en cuivre séparés par deux lames isolantes placées dans un plan orthogonal au plan des spires; l'organe ainsi réalisé est solidaire du rotor; il est appelé collecteur ; deux balais en carbone placés sur l'axe des pôles et solidaires du stator frottent sur ce collecteur, constituant les contacts glissants pour accéder au bobinage induit. Les extrémités de chacune des deux spires du bobinage sont reliées aux deux lames du collecteur.

Nous pouvons alors schématiser le bobinage suivant la fig.5.a où chaque générateur de tension a la même f.é.m alternative e. Nous constatons que le bobinage induit est fermé sur lui-même et formé de deux branches identiques en parallèle de f.é.m 2.e; chaque branche est appelée voie d'enroulement. Le balai B1 est relié aux pôles négatifs des générateurs et le balai B2 aux pôles positifs.

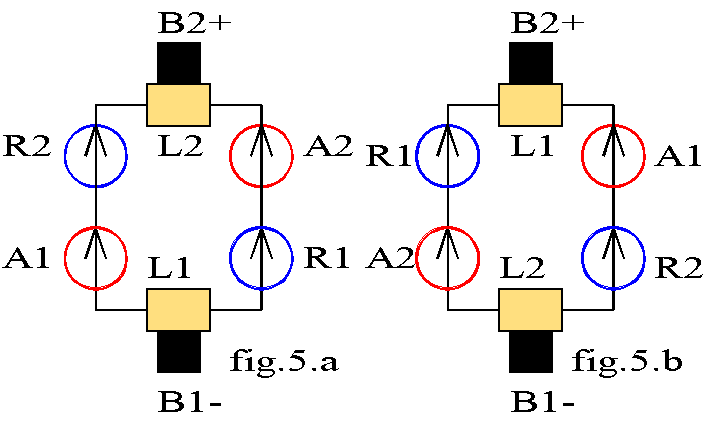
Supposons que l'induit effectue un demi-tour; durant ce demi-tour la f.é.m par barre évolue suivant

e(t) =L.v.B(W.t +qo); elle s'annule lorsque la barre passe sur la ligne neutre puis s'inverse lorsque celle-ci change de pôle; à la fin du demi-tour les conducteurs A1 et A2 d'une part, R1 et R2 d'autre part ont permuté; les lames du collecteur ont suivi la rotation du rotor donc ont permuté mais les balais sont restés fixes. Le bobinage peut alors être schématisé suivant la fig5.b; nous constatons que la polarité des balais est restée la même; par le jeu du collecteur, nous recueillons donc entre les balais une f.é.m égale à |2.e | représentée en trait fin sur la fig3. Cette f.é.m n'est pas continue mais est de valeur moyenne non nulle; le collecteur joue le rôle d'un redresseur double alternance.

Pour augmenter l'amplitude de cette f.é.m, nous devons augmenter le nombre de barres par encoches; pour pouvoir garder le même principe de bobinage, le nombre de barres par encoches 2.z est pair; dans chaque encoche, z conducteurs A1, ..., Az servent de conducteur d'aller et les z autres R1, ..., Rz servent de conducteurs de retour. L'ensemble de z conducteurs d'aller ou de retour forme un faisceau. Prenons les 2.z conducteurs de cette encoche et ceux A'1, ...,A'z, R'1, ..., R'z de l'encoche distante d'un pas polaire; le bobinage se fait en reliant A1 à la lame L1 par l'avant et à R'1 par l'arrière, R'1 à A2 par l'avant, sans passer par le collecteur ... A'z est relié par l'arrière à R'z et R'z est connecté par l'avant à la lame L2. On fait de même avec les conducteurs R1, A'1, R2, ... La f.é.m d'un faisceau est alors 2.z.e et celle de la machine |2.z.e| (fig.6a).

Pour diminuer l'ondulation, nous utilisons un grand nombre d'encoches par pôles; les f.é.m des conducteurs situés dans des encoches différentes sont déphasées en raison de la répartition spatiale. Prenons par exemple quatre encoches décalées de p /2. Les f.é.m des conducteurs de deux encoches consécutives sont en quadrature; si nous faisons des spires couvrant un pas polaire en bobinant un faisceau aller de l'encoche 1, un faisceau de retour de l'encoche 3 décalée de p , un faisceau aller de l'encoche 2 décalée de p /2 par rapport à 1 et un faisceau de retour de l'encoche 4 opposée à 2, la f.é.m de la voie sera obtenue en ajoutant deux tensions redressées du type de la f.é.m de voie de la fig.3 décalées d'un quart de période; sur la fig.6b nous obtenons la f.é.m de la machine:

Enroulement d'une machine bipolaire

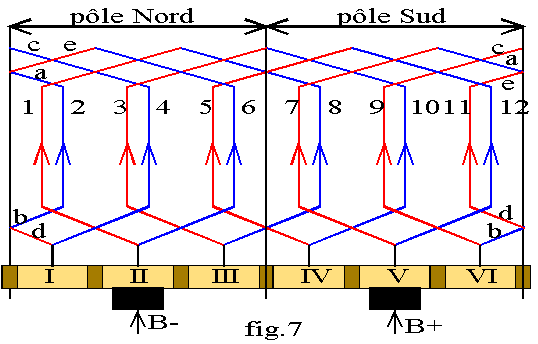
Nous représentons le bobinage d'une machine à 2 pôles en développant le cylindre d'induit; la machine à six encoches; dans chaque encoche nous représentons le faisceau d'aller et celui de retour en les décalant légèrement (fig.7). Les flèches représentent le sens positif de la f.é.m. par barre. Partant du faisceau d'aller 1 nous le relions par l'arrière au faisceau de retour diamétralement opposé soit le faisceau 8; la liaison par l'avant se fait sur la lame collecteur III; nous continuons le bobinage en utilisant le faisceau d'aller de l'encoche suivant la première utilisée soit le faisceau 3. Pour faire cette première spire, la liaison par l'arrière se fait en progressant de 7 faisceaux; nous dirons que le pas arrière est y₁= 7; la liaison par l'avant passe par le collecteur et recule de 5 faisceaux, nous dirons que le pas avant est y₂= -5 ; nous continuons le bobinage en utilisant ces pas: 3Þ10Þlame IVÞ5Þ12Þ lame VÞ7; nous avons alors relié deux conducteurs d'un même pôle; sur la lame V les f.é.m s'opposent; nous avons atteint l'extrémité d'une voie; cette lame est en contact avec le balai B +; nous continuons le bobinage: 7Þ7+7=14 =2 car la disposition des encoches est cyclique Þ lame VIÞ 2-5=-3=9

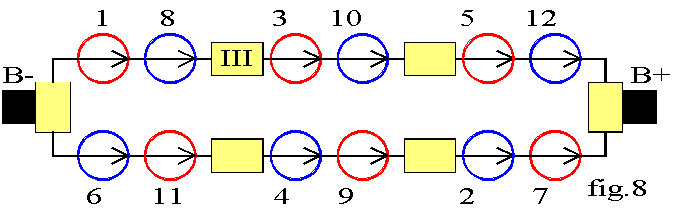
A la lame II sont reliés les faisceaux 1 et 6 du même pôle; c'est l'autre extrémité de la voie; cette lame est en contact avec le balai B -. Nous pouvons donner fig.8 une schématisation de l'enroulement. Ce type d'enroulement avec des pas arrière et avant de signes opposés est dit imbriqué . Il comporte toujours 2.a =2 voies en parallèle pour une machine à 2 pôles.

Enroulement de machine multipolaire

Plusieurs types d'enroulement sont alors possibles; nous pouvons réaliser une enroulement imbriqué simple du type de celui de la machine bipolaire. Un tel enroulement comporte toujours 2 voies; la f.é.m est donc créée par la moitié des faisceaux et le courant circulant I entre les balais se répartit par moitié entre les voies.

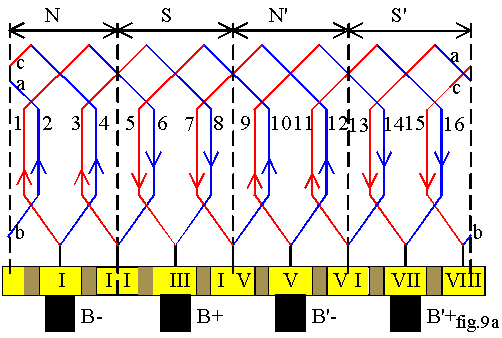
Nous pouvons réaliser un enroulement imbriqué multiple comme celui développé sur la fig.9a :

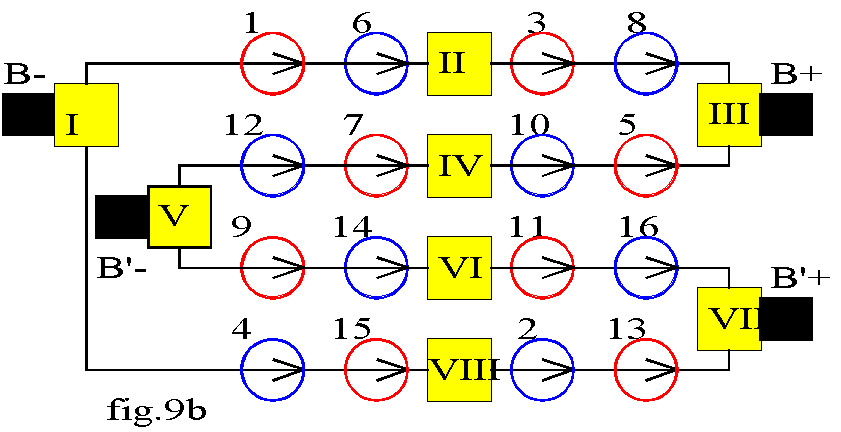
la machine possède 2p =4 pôles et 8 encoches; nous adoptons un pas arrière y1=5 et un pas avant y2= -3; nous réalisons le bobinage: 1Þ6 Þlame II Þ 3Þ 8 Þ lame IV Þ 5 ; 5 et 8 étant sous le même pôle S, la lame IV est en contact avec un balai B +. Nous poursuivons de même le bobinage. Nous obtenons un bobinage à 2a = 4 voies en parallèle ; chaque voie comporte quatre faisceaux ; il y a quatre balais reliés deux à deux (fig.9b).

Nous pouvons constituer un enroulement ondulé en utilisant deux pas de même signe; cette enroulement peut être simple avec 2 voies ou multiples avec plus de deux voies.

La fig.10 donne le développement d'un enroulement ondulé simple pour une machine à 4 pôles et 13 encoches;

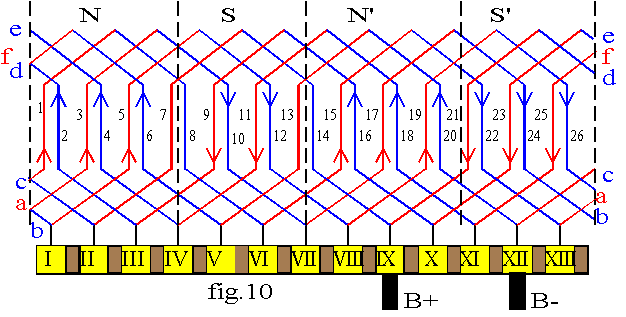
les conducteurs 7 et 8 d'une même encoche sont situés sous une ligne neutre; leur f.é.m. est nulle; il en est de même pour 13 et 14; le pas arrière est y₁= 7 et le pas avant y₂ = 7. Le faisceau 1 sous le pôle N est relié à 8 sous la ligne neutre; 8 est relié à 15 sous le pôle N' en passant par la lame VI du collecteur; 15 est relié à 22 sous le pôle S'; en passant par la lame XIII nous revenons à 3 sous le pôle N... Sur la lame IX sont reliés 14 et 21; nous avons alors changement de signe des f.é.m de barre donc une extrémité des voies reliées au balai B+; sur la lame XII sont reliés 20 du pôle N' et 1 du pôle N; nous avons donc l'autre extrémité des voies reliée au balai B-.

Cet enroulement ondulé simple possède donc bien deux voies.

Dans tous les cas :

Le bobinage d'induit est fermé sur lui-même. Il répartit les 2.Ne faisceaux des Ne encoches d'induit en 2.a voies d'enroulement de Ne/a faisceaux bobinés en série; les 2.a voies sont placées en parallèle entre les balais de la machine; la f.é.m. de la machine est égale à celle créée dans une voie et le courant d'induit I se répartit également entre les voies parcourues par l'intensité I / 2.a.

Pour une même machine l'augmentation du nombre de voies réduit la f.é.m. et le courant dans chaque conducteur; les machines haute tension auront donc généralement deux voies et les machines basse tension, fort courant, auront un nombre de voies plus élevé.

Pour une machine ayant un nombre d'encoches et un nombre de pôles fixés, tous les modes de bobinages ne sont pas possibles; chaque type de bobinage impose une relation entre le nombre d'encoches et le nombre de pôles.

2.1 Machine bipolaire

Soit une machine à 2.p = 2 pôles; le nombre de voies est toujours 2.a = 2. Soit Ne le nombre d'encoches; chaque encoche contient deux faisceaux de z conducteurs chacun.

La f.é.m E de la machine est créée par les conducteurs d'une voie, c'est à dire par la moitié des conducteurs; on peut considérer que tout se passe comme si tous les conducteurs situés sous le même pôle formaient la voie.

Lorsque le rotor tourne à la vitesse angulaire W les encoches défilent devant les pôles du stator; supposons qu'à l'instant t = 0, les encoches 1, 2,..., Ne/2 soient sous le pôle Nord et les encoches (Ne/2)+1,..., Ne sous le pôle Sud; les encoches étant régulièrement réparties, elles sont décalées angulairement de l'angle a = 2.p/Ne ;

à l'instant Dt = a/W, le rotor a tourné de l'angle a; l'encoche 1 a pris la place de l'encoche 2, 2 de 3, ..., Ne de 1. Il y a toujours Ne /2 encoches sous le pôle Nord avec une répartition spatiale identique à celle de l'instant t = 0; si le nombre d'encoches est suffisamment élevé a est très petit devant 2.p et Dt est très petit devant la période de rotation ; durant ce temps les encoches se déplacent en bloc donc la f.é.m de la machine varie légèrement puis

E(0) = E(Dt).

La répartition des encoches peut être considérée comme quasi stationnaire.

La barre numéro i placée en un point d'angle polaire q sous le pôle Nord coupe durant Dt le flux stator DFi ; la f.é.m induite dans cette barre est en valeur absolue: ei = DFi(q)/Dt ; tous les conducteurs d'un faisceau de cette encoche ont le même angle polaire et sont bobinés en série; la f.é.m créée par ces z barres est donc:

efi = z.ei = z.DFi(q)/Dt ; la f.é.m des conducteurs de l'encoche i est eei = 2.z.DFi(q)/Dt ; la f.é.m E de la machine est la somme des f.é.m des faisceaux des encoches 1 à Ne/2. Il vient donc E = S eei pour i variant de 1 à Ne/2. D'où : E =2.z.Sei soit : E= 2.z.S[DFi(q)/Dt].

Lors du déplacement angulaire a les encoches de la voie balayent la surface totale d'un pôle; il vient donc SDFi(q) = Fp flux utile créé par un pôle; nous obtenons la f.é.m : E = 2.z.Fp /Dt ; Dt = a /W = 2.p/W.Ne ; en utilisant la vitesse de rotation n exprimée en tr.min^-1, il vient W = 2.p.n / 60 et Dt = 60/n.Ne ; d'où E = (2.z.Ne).(n/60).Fp ; chaque encoche contenant 2.z barres, (2.z.Ne) = N nombre total de conducteurs du bobinage induit.

Nous obtenons l'expression finale de la f.é.m : E = N.(n/60).Fp

2.2 Machine multipolaire

Soit une machine ayant 2.p pôles et 2.a = 2 voies; le raisonnement mené ci-dessus reste inchangé en raisonnant en angle électriques; le décalage en angle électrique entre deux encoches est ae = p.a ; il vient alors Dt = a / W = ae/p.W ; Dt devient donc p fois plus petit; cette quantité intervenant au dénominateur dans l'expression de E, la f.é.m devient p fois plus grande:

Lorsque le bobinage contient 2.a voies au lieu de 2 voies, le nombre de conducteurs par voie est divisé par a; la f.é.m est donc aussi divisée par a; il vient: E = (p/a).N(n/60).Fp .

Soit une machine possédant 2p pôles dont les N conducteurs de l'induit sont répartis en 2.a voies; le flux Fp est le flux utile créé par un pôle du stator; le rotor tournant à la vitesse n exprimée en tours par minute , la f.é.m mesurée à vide entre les balais est :

2.3 Caractéristique à vide

Pour une machine donnée, le coefficient k' = p/60.a est constant; il vient alors :E = k'.n.Fp .

Si nous voulons utiliser la vitesse angulaire W = 2.p.n / 60, il vient:

E = (30.k'/p).Fp = k.W.Fp en posant k = 30.k'/p.

Pour une machine excitée par des aimants permanents le flux F_p est constant; dans ce cas la f.é.m est directement proportionnelle à la vitesse: E = K'.n = K.W avec K= k.Fp .

Pour une machine à stator bobiné et alimenté par un courant continu d'intensité Iex , le flux est fonction de cette intensité; nous avons alors E = k'.n.f(Iex ). La fonction f(Iex) liant le flux utile par pôle et le courant créateur est donnée par la caractéristique réluctive du circuit magnétique; c'est une caractéristique magnétique présentant les phénomènes de saturation et d'hystérésis; la réluctance de l'entrefer étant prépondérante dans celle du circuit total, ces phénomènes sont peu marqués en particulier celui d'hystérésis.

A vitesse constante, la caractéristique à vide E(Iex) reproduit la caractéristique réluctive (fig.11) avec son hystérésis.

La caractéristique à vide Cv est la caractéristique moyenne du cycle. Pour un courant d'excitation nul, les pôles gardent une aimantation rémanente qui crée la f.é.m rémanente Er

3 Principe de fonctionnement

3.1 Existence d'un couple électromagnétique

La machine étant excitée, un flux par pôle Fp existe dans l'entrefer; créons un courant continu d'intensité I entre les balais de l'induit. Chaque conducteur d'une voie est parcouru par un courant d'intensité Ib = I/2.a. Par le jeu du collecteur, tous les conducteurs sous un pôle sont parcourus par un courant de même sens et ce sens change lorsque le nom du pôle change. Si l'induit tourne, les conducteurs défilent devant les pôles mais comme pour la répartition des f.é.m., la répartition des courants de barre est quasi stationnaire : sous un pôle donné il y a toujours le même nombre de conducteurs ayant les mêmes courants.

Représentons fig.12 une machine bipolaire;

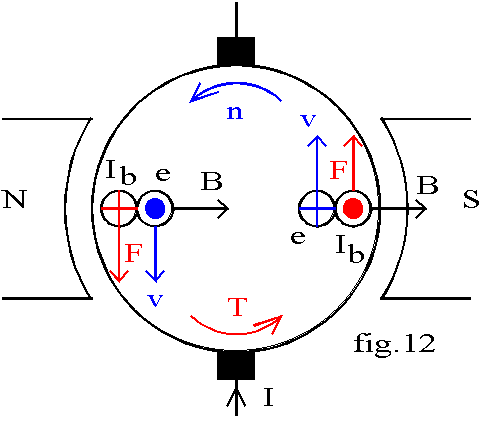
Supposons que l'intensité du courant induit soit dirigée vers l'arrière sous le pôle Nord donc vers l'avant sous le pôle Sud. Le vecteur champ B est de direction radiale, sortant du pôle Nord pour rentrer par le pôle Sud. Par la règle des trois doigts, nous traçons la direction et le sens de la force électromagnétique F exercée sur chaque barre; l'intensité de cette force est F = B.Ib.L où L représente la longueur de la barre. Les forces sur les conducteurs de deux pôles sont de même direction mais de sens opposés; elles constituent un couple de moment T = 2.ri.F avec ri rayon de l'induit. Ce couple tend ici à faire tourner l'induit dans le sens direct.

Notons que le moment du couple ne dépend que de paramètres géométriques, de l'induction et du courant induit; il est indépendant du mouvement de l'induit puisque la répartition des courants est quasi stationnaire.

3.2 Réversibilité des échanges d'énergie

La charge mécanique exerce sur l'arbre de la machine un couple dont le moment compté positivement dans le sens inverse est T' . Soit J le moment d'inertie, par rapport à l'axe de rotation, de l'ensemble des parties tournantes (machine et charge). La relation fondamentale de la dynamique des corps en rotation donne : J.dW/dt = T - T' , W et T étant comptés positivement dans le sens direct.

La machine étant initialement à l'arrêt , nous avons alors deux cas:

si T - T' > 0 ; nous avons alors dW/dt > 0; la vitesse angulaire augmente et la machine démarre dans le sens direct (flèche n dans le même sens que flèche T). Les conducteurs ont à un instant donné la vitesse tangentielle

v = ri.W représentée sur la fig.12. Le déplacement des barres dans le champ B crée une f.é.m induite e =B.L.v; d'après la loi de Lenz, cette f.é.m. a un sens tel qu'elle s'oppose par ses effets à la cause lui donnant naissance c'est à dire à la rotation de l'induit; elle tend donc à créer un courant de sens opposé à Ib dans chaque barre; d'où le sens de e indiqué sur la fig.12; cette f.é.m. est ici une force contre-électromotrice et la machine fonctionne en récepteur d'énergie électrique (e et Ib de sens opposés) et en générateur d'énergie mécanique ( n et T de même sens). La tension à appliquer entre les balais pour faire circuler le courant I est donnée par la loi de Pouillet:

U = E +R.I avec R résistance du bobinage induit. Si la tension U est maintenue constante dans le temps l'augmentation de vitesse augmente la f.é.m. donc réduit l'intensité et le couple. Si nous supposons le couple de charge T' indépendant de la vitesse, T-T' diminue et s'annule à un instant t >0; à cet instant dW/dt =0 donc la vitesse devient constante; le régime permanent est atteint.

si T - T' < 0: nous avons dW/dt < 0 donc démarrage de la machine dans le sens trigonométrique négatif ; le sens du courant étant inchangé, le sens du couple reste inchangé et se trouve opposé à celui de la vitesse n. Le vecteur vitesse v s'inverse donc la f.é.m induite dans chaque barre aussi pour créer une force de sens opposé à v; dans une barre f.é.m. e et intensité I_b ont le même sens; la machine fonctionne en générateur d'énergie électrique (e et Ib de même sens) et en récepteur d'énergie mécanique ( n et T de sens opposés). La tension à appliquer entre les balais pour faire circuler le courant I est donnée par la loi de Pouillet; en gardant le même sens conventionnel pour U, il vient: U = -E -R.I soit U < 0.

Dans une machine à courant continu dont le flux est imposé, l'intensité du courant induit fixe en grandeur et signe le moment du couple T créé ; si T' est le moment du couple de charge, le signe de T-T' fixe alors le sens de rotation de l'arbre et le signe de la f.é.m induite E. Si nous nous imposons une valeur de la vitesse n, celle-ci fixe la valeur de E donc la valeur de la tension d'induit U. La machine fonctionne en moteur si T et n ont le même sens et en générateur si T et n sont de sens opposés.

Si nous imposons le flux inducteur et la tension d'induit U, la f.é.m E est peu différente de U donc est quasi constante; par E = K'.n , nous voyons que la tension impose quasiment la vitesse n; supposons n positive par exemple. La charge et la vitesse étant connues, le couple de charge T' est connu. En régime permanent, la charge imposera donc T = T'; le couple est alors fixé donc le courant d'induit est imposé.

4 Fonctionnement en charge

4.1 Réaction magnétique d'induit

Lorsque la machine fonctionne en charge, les conducteurs de l'induit sont parcourus par le courant continu I/2.a; le sens de ce courant est opposé à celui de la f.é.m dans le cas d'un fonctionnement moteur (f.c.é.m. d'un récepteur) ou dans le sens de la f.é.m. pour un fonctionnement générateur; la répartition de courant est donc identique au sens près à celle de la f.é.m.; en particulier le sens des courants de barre change sous chaque pôle; par le jeu du collecteur la répartition des courants induits est quasi stationnaire.

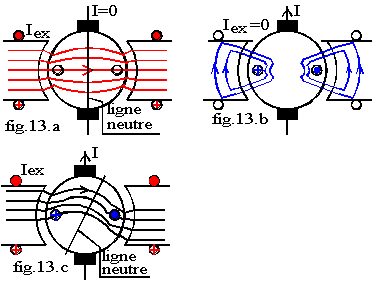
Du point de vue magnétique l'induit se comporte comme une armature fixe à 2.p pôles alimentée par un courant continu. Il crée donc un champ fixe dans le temps et variable dans l'espace de même type que le champ créé par le stator. Ces deux champs se combinent pour donner le champ résultant en charge. Le champ magnétique en charge est différent de celui à vide; cette modification du champ donc du flux modifie la f.é.m de la machine. Cette modification de flux est appelée réaction magnétique d'induit.

La fig.13 donne l'allure du spectre magnétique de la machine: sur la fig.13.a le stator est seul alimenté, nous voyons le spectre du champ inducteur; sur la fig.13.b le rotor est seul alimenté, nous voyons le spectre du champ de l'induit; la fig.13.c donne le spectre résultant des précédents lorsque la machine est excitée et en charge.

Si la machine fonctionne en moteur, les sens des courants étant ceux de la fig.13.c, l'induit tourne dans le sens direct. La distorsion des lignes de champ par réaction magnétique d'induit crée dans un moteur :

un renforcement du champ sous les cornes polaires d'entrée, c'est à dire sous la pointe du pôle par laquelle les conducteurs d'induit rentrent sous le pôle; inversement le champ est affaibli sous les cornes polaires de sortie.

une rotation de la ligne neutre, sur laquelle le champ est nul, dans le sens inverse du sens de rotation

4.2 f.é.m. en charge de la machine continue

La distorsion du champ crée un affaiblissement global du flux par pôle; en effet en raison de la saturation, les ampères-tours d'induit qui s'ajoutent aux ampères-tours inducteurs sous les cornes d'entrée ne compensent pas la différence des ampères-tours sous les cornes de sortie (fig.14).

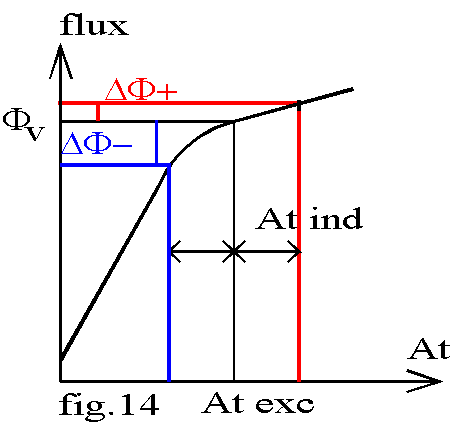
Pour un même courant inducteur le flux résultant en charge est toujours inférieur au flux à vide.

Les balais sont calés sur l'axe des pôles ; à vide, ils sont sur la ligne neutre et tous les conducteurs d'un pôle donc d'une voie ont la même f.é.m eb ; la rotation de la ligne neutre en charge, modifie le sens de la f.é.m. dans les conducteurs de la voie qui sont proches de la ligne neutre. Sur la fig.15 , les conducteurs de 1 à 9 appartiennent toujours à la même voie mais ont des f.é.m. opposées; la f.é.m. de la machine est la somme de celles de ces conducteurs; en admettant que le champ est constant sous un pôle tous les conducteurs ont en valeur absolue la même f.é.m. eb. A vide la f.é.m. de la machine est celle de 9 conducteurs donc Ev = 9.eb. En charge la f.é.m sera: Ech = 8eb - eb = 7.eb .

La rotation de la ligne neutre réduit également la f.é.m. en réduisant le nombre de conducteurs efficaces pour créer la f.é.m de la voie.

La réaction magnétique d'induit réduit le flux dans la machine; à vide le flux est Fp sous un pôle; en charge il sera Fch < Fp ; la différence entre les flux est une fonction croissante du courant d'induit I; la f.é.m est proportionnelle au flux; elle sera donc plus faible à vide qu'en charge; à vide la f.é.m est Ev = k W Fp ; en charge elle devient Ech = k W Fch ; nous posons e = Ev - Ech = k.W.(Fp - Fch); cette d.d.p. e est toujours positive; elle est appelée chute de tension par réaction d'induit.

Cette quantité est proportionnelle à la vitesse et fonction par les flux des intensités des courants Iex dans l'inducteur et I dans l'induit. La chute est maximale lorsque le courant d'excitation correspond au coude de la caractéristique à vide.

4.3 Compensation de la réaction d'induit

Pour compenser la modification du flux en charge, il faut disposer d'un enroulement auxiliaire créant une induction opposée à celle de l'induit. Pour avoir une répartition semblable à celle de l'induit, on découpe des encoches parallèles à celles de l'induit dans les épanouissements polaires; les barres placées dans ces encoches sont connectées en série avec l'induit avec un sens tel qu'elles créent des ampères tours opposés à ceux de l'induit. On dit alors que la machine est compensée. Le flux est alors quasi indépendant de la charge; l'augmentation de la résistance d'induit apportée par le bobinage de compensation fait perdre une partie de l'avantage obtenu en compensant la machine.

5 Phénomènes de commutation

5.1 Mise en évidence

Lorsqu'une barre change de pôle, l'intensité du courant dans la barre doit s'inverser; nous dirons qu'il faut commuter l'intensité dans la barre. La commutation se fait en trois phases suivant fig.16.

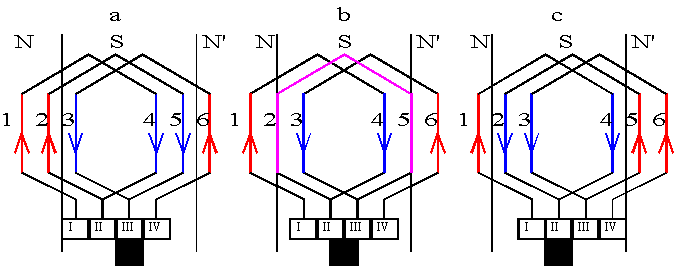
Sur la fig.16.a, la spire 2-5 a une f.é.m. indiquée par les flèches dans le sens horaire; pour un moteur, elle est parcourue par une intensité dans le sens inverse, le balai est sur la lame III du collecteur. L'induit se décalant vers la droite par rapport aux pôles, sur la fig.16.b, les conducteurs 2 et 5 sont chacun sous une ligne neutre; la f.é.m. de la spire est nulle; le balai est à cheval sur les lames II et III et court-circuite la spire 2-5; sur la fig.16.c les conducteurs 2 et 5 ont changé de pôle, la f.é.m et l'intensité se sont inversées dans la spire.

La commutation c'est à dire le passage de a à c dure environ 1ms; pendant la phase b, la f.é.m est nulle dans la spire étudiée mais pas l'intensité; en effet l'inductance propre de la spire s'oppose à la variation du courant. Lorsque le balai quitte la lame III, il force le courant à s'inverser; si l'inversion n'est pas finie avant cet instant, le courant varie très rapidement donc la f.é.m. d'auto-induction très élevée crée une étincelle d'extra-rupture entre la lame III et le balai; ces étincelles de commutation détériorent balai et collecteur et génèrent des parasites radioélectriques.

5.2 Amélioration de la commutation

Les défauts de commutation viennent de la difficulté à inverser rapidement l'intensité dans un circuit très inductif. Pour faciliter cette inversion nous pouvons essayer de créer, lors du passage des barres sous la ligne neutre, une f.é.m. ayant le sens de l'intensité après la commutation; durant la phase b, cette f.é.m. s'opposera au courant et donc le fera diminuer plus rapidement. Dans le cas de la figure, la f.é.m. doit avoir le sens trigonométrique inverse dans la spire 2-5; pour créer cette f.é.m. nous utilisons des pôles auxiliaires de faible section et placés sur les lignes neutres donc entre les pôles principaux (fig.1). Sous un pôle N, la f.é.m. est donc dirigée de bas en haut; dans la position b, le pôle auxiliaire doit créer en 2 une f.é.m. vers le haut, ce doit donc être un pôle Nord; de même un autre pôle auxiliaire doit créer dans 5 une f.é.m vers le bas; ce doit donc être un pôle Sud. En moteur le pôle auxiliaire doit avoir le nom du pôle que l'on vient de quitter. Pour adapter automatiquement l'effet des pôles auxiliaires au courant d'induit à commuter, ces pôles sont excités par le courant d'induit; ils sont donc connectés en série avec l'induit. Ils vont augmenter la résistance de l'induit mais aussi les fuites magnétiques entre les pôles principaux: la présence de fer dans le circuit de fuites réduit sa réluctance donc augmente le flux; malgré ces défauts, les pôles auxiliaires sont indispensables dès que la puissance de la machine est de l'ordre du kW.

6 Bilan des pertes de la machine continue

6.1 Pertes mécaniques

Les pertes mécaniques se décomposent en:

è pertes par frottements secs sur les paliers portant l'arbre rotor et entre balais et collecteur. Ces pertes sont proportionnelles à la vitesse de rotation n: pmf = a.n.

è pertes par ventilation dues aux frottements fluides dans l'écoulement de l'air dans l'entrefer et à l'éventuel ventilateur porté par l'arbre pour un refroidissement plus efficace des conducteurs. Ces pertes sont proportionnelles au carré de la vitesse : pmv =a'.n^² .

Les pertes mécaniques globales sont donc pmec = pmf + pmv = a.n +a'.n^² .Nous supposons ces pertes indépendantes de la charge mécanique de la machine ce qui n'est pas tout à fait exact car le couple modifie l'effort sur les paliers donc pmf et l'intensité du courant modifie la température donc l'écoulement de l'air donc pmv .

6.2 Pertes dans le circuit magnétique

Ces pertes se décomposent en :

è pertes par hystérésis : chaque point du rotor de la machine est soumis à une induction périodique; l'induction reprend la même valeur lorsque le rotor a tourné de deux pas polaires soit de 2.p/ 2.p = p/p; à la vitesse angulaire W le temps mis pour tourner de cet angle est T = p/p.W période temporelle de l'induction en un point du rotor; la fréquence de variation du champ est donc : f = p.W /p = p.n/30 = a n. Les pertes par hystérésis sont de la forme

ph = hh.V.f.Bmax² où hh est le coefficient de Steinmetz des tôles du rotor et V le volume des tôles; ces pertes sont proportionnelles à la vitesse par la fréquence f et au carré du flux par l'induction maximale: ph = c.n.F^² En faisant intervenir la f.é.m E = k'.n.F , nous obtenons ph = d.E^²/ n .

è pertes par courants de Foucault ; ces pertes se localisent dans le fer du rotor, dans les barres de l'induit et dans les épanouissements polaires à cause du papillotement des lignes de champ dû à la succession des dents et des encoches devant les pôles; la réluctance des encoches étant très grandes devant celles des dents, les lignes de champ ont tendance à suivre la dent dans sa rotation puis à sauter brusquement sur la dent précédente. Ces pertes sont de la forme: pcF = h'.V.f^².Bmax^² ; nous pouvons donc, comme ci-dessus écrire: pcF = c'.n^².F^² = d'.E^² .

Les pertes dans le fer dépendent donc de la vitesse n et du flux donc des intensités des courants inducteur et induit (par réaction magnétique d'induit). Nous pouvons écrire : pfer = ph +pcF = (c.n +c'.n^²).F^² = d.E^² /n+ d'.E^² .

Ces relations ne sont valables que si la machine n'est pas trop saturée; pour une forte saturation les pertes dans le fer augmentent avec le flux plus fortement que suivant la relation pfer = b.F^².

6.3 Pertes par effet Joule

Ces pertes dans les conducteurs de la machine se décomposent en:

è pertes dans l'inducteur : ces pertes comprennent les pertes dans la résistance de l'inducteur Re.Iex^² et les pertes dans les organes de réglage du courant inducteur: rhéostat d'excitation ,redresseurs ...

è pertes dans l'induit : ces pertes comprennent les pertes dans le bobinage, le collecteur, les balais, les pôles auxiliaires et les connexions. Elles sont de la forme: pja = R.I^² avec R résistance totale entre bornes d'induit parcouru par le courant d'intensité I. La résistance de l'induit est fonction de la température de fonctionnement donc de la charge; la résistance de contact balai-collecteur dépend du courant I traversant le contact; elle est beaucoup plus élevée à faible courant qu'à fort courant.

6.4 Pertes supplémentaires

Ces pertes n'existent qu'en charge; elles prennent en compte toutes les pertes que l'on ne sait classer ailleurs Par exemple la modification des pertes mécaniques avec la charge, la modification des pertes par effet Joule due à l'effet de peau dans les conducteurs de l'induit. . .

6.5 Bilan des puissances

Faisons le bilan des puissances dans l'induit de la machine continue:

ven moteur : le réseau fournit la puissance électrique Pelec = U.I . Après décompte des pertes par effet Joule dans l'induit, il reste la puissance électromagnétique Pem = U.I - R.I^² = E.I

Les pertes dites constantes : pc = pmec+ pfer sont ensuite décomptées pour obtenir la puissance mécanique utile

Pu = Pmec .

Le rendement d'induit est ha = Pu / Pelec.

Pour obtenir le rendement de la machine, il faut ajouter à la puissance absorbée, les pertes d'excitation :

h = Pu / (Pelec + Pex ).

Aux puissances, nous pouvons associer des couples par la relation P = T.W ; nous définissons ainsi

è le couple électromagnétique de moment Tem = Pem / W

è le couple de pertes de moment Tp = pc / W

è le couple utile de moment Tu = Pu / W .

Le bilan de puissance donne la relation sur les couples : Tu = Tem - Tp .

ven génératrice : le bilan de puissance s'inverse ; la puissance mécanique est la puissance absorbée, la puissance électrique Pelec = Pmec - pc - pja = U I.

Le rendement est : h = Pelec / (Pmec + Pex ). Le couple absorbée sur l'arbre est Tab = Tem + Tp.