"Machine asynchrone"

Chapitre 4.1

Principes

1 Principe

1.1 Constitution

rotor bobiné : le bobinage est alors semblable à celui du stator : il comporte q' phases (généralement q' = 3) et obligatoirement le même nombre de pôles que le stator. Ce bobinage, le plus souvent couplé en étoile, est relié à des bagues de cuivre solidaires du rotor sur lesquelles frottent des balais solidaires du stator.

1.2 Principe de fonctionnement

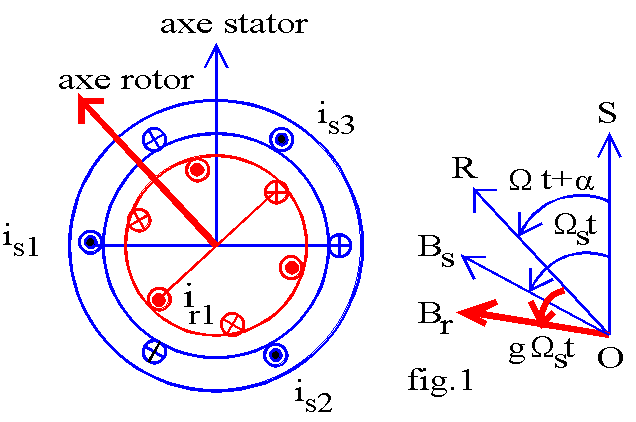
Le stator alimenté par un réseau triphasé équilibré de fréquence f crée un champ B_s tournant à la vitesse de synchronisme

n_s = 60.f / p.

Comparé au transformateur statique, le transformateur à champ tournant à l'inconvénient de pertes plus élevées en raison de l'entrefer qui augmente le courant magnétisant; il a l'avantage de permettre un déphasage quelconque entre les f.é.m. primaires et secondaires.

Cet avantage est utilisé dans le régulateur d'induction pour réaliser un transformateur à rapport variable; le stator est alimenté par un réseau triphasé, la charge est branchée aux bornes du stator et du rotor connectés en série; en négligeant les chutes de tension, la tension aux bornes de la charge est E₂ + E₁ = ( 1 + m ).E₁. Pour m = 1, en faisant varier le décalage mécanique a de p à 0, la tension charge varie de 0 à 2.E₁. Pour interdire la rotation du rotor en charge, un système de vis sans fin permet de décaler le rotor tout en interdisant sa rotation.

Au synchronisme, le glissement est nul et à l'arrêt le glissement est égal à 1. Lorsque le moteur fonctionne à vide, le glissement varie de 0,1 à 2 % et en charge nominale de 1 à 15 %; ce glissement est d'autant plus faible que la puissance nominale est élevée

1.3 Champs magnétiques en charge

Le stator crée le champ B_s tournant à la vitesse angulaire de synchronisme W_s par rapport au stator; le rotor tournant à la vitesse W dans le sens de B_s, ce champ tourne à la vitesse W_s - W soit g.W_s par rapport au rotor. Les courants induits au rotor sont de pulsation électrique w' = p.g.W_s = g.w_s donc de fréquence f ' = g.f.

Le champ rotorique B_r créé par ces courants tourne à la vitesse w' / p = g.W_s par rapport au rotor donc à la vitesse g.W_s + W = Ws par rapport au stator. On retrouve le principe fondamental des machines : une machine ne peut fonctionner que si le rotor et le stator crée des champs de même nature.

Si nous négligeons l'impédance interne du stator, la f.é.m par phase est égale à la tension simple :

V₁ = 2,22.K₁.N₁.f.F; le flux par pôle est F = k.(V₁ / f ) . Le flux ne dépend donc que du réseau alimentant le stator ; comme un transformateur statique, la machine asynchrone fonctionne à flux forcé. Il n'y a donc pas de réaction magnétique d'induit; en charge, le courant stator appelé est la somme du courant magnétisant et du courant de travail qui compense les ampères-tours rotoriques.

La f.é.m induite au rotor est E₂ = 2,22.K₂.N₂.f '.F; le rapport de transformation est alors :

E₂ / E₁ = K₂.N₂.f ' / K₁.N₁.f = g.m ; il est proportionnel au glissement.

La machine asynchrone est une machine à flux forcé par la tension statorique : F = k.( V₁ / f ); les champs créés par le stator et le rotor sont synchrones : ils tournent à la vitesse de synchronisme n_s par rapport au stator et à la vitesse g.n_s par rapport au rotor; les grandeurs induites au rotor sont de fréquence f ' = g.f.

2.1 Équations du stator

Le modèle équivalent à une phase du moteur asynchrone est identique à celui du primaire d'un transformateur statique ( fig.2)

j₁₀ est le courant stator lorsque le courant rotor est nul c'est à dire lorsque rotor est ouvert ou lorsqu'il tourne au synchronisme.

Les équations sont :

2.2 Équations du rotor

Le rotor tournant à la vitesse g.Ws par rapport aux champs stator et rotor est le siège de pertes dans le fer; les pertes sont proportionnelles à la fréquence pour les pertes par hystérésis et au carré de la fréquence pour celles par courants de Foucault; dans la plupart des cas, le glissement est petit devant 1 donc la fréquence rotorique f ' = g.f est petite devant f : nous négligeons les pertes dans le fer du rotor lorsque le glissement est petit devant 1

Le rotor admet alors le schéma équivalent de la fig.3 :

Les équations sont :

2.3 Modèle équivalent à une phase

Contrairement à l'étude faite pour le transformateur statique, nous ne pouvons pas rassembler les modèles et les équations du stator et du rotor car les grandeurs n'ont pas toutes la même fréquence. Divisons les équations (4) et (5) par le glissement; il vient :

En valeur efficace, nous avons un rapport de transformation g.m donc E₂ / E₁ = g.m d'où E₂ / g = m.E₁. Nous pouvons alors interpréter les équations (6) et (7) comme les équations au secondaire d'un transformateur statique de rapport m et de résistance par phase R₂ / g, toutes les grandeurs ayant la fréquence f. Pour rassembler les grandeurs sur un même schéma, nous remplaçons j₂ de fréquence g.f par j'₂ de fréquence f et de même valeur efficace, e₂ par e'₂ de fréquence f et de valeur efficace E₂ / g. L'équation électrique devient alors :

.

Nous pouvons maintenant modéliser une phase suivant le modèle du transformateur statique (fig.4):

TP représente le couplage entre le stator et le rotor; c'est un transformateur parfait de rapport constant m.

Le modèle d'une machine asynchrone est identique à celui du transformateur statique, à condition de diviser la résistance secondaire par le glissement g.

Ce modèle ne peut être utilisé en pratique en raison de la difficulté à connaître les inductances de fuites. Comme pour le transformateur statique, nous pouvons utiliser l'hypothèse de Kapp, c'est à dire transférer la bobine modélisant le circuit magnétique "en tête "; nous obtenons la fig.5.

Cette hypothèse consistant à négliger la chute de tension créée au stator par j₁₀ est moins bien vérifiée que dans le transformateur statique; la présence de l'entrefer augmente le courant magnétisant qui peut atteindre 40 à 60 % du courant nominal; elle est cependant fréquemment utilisée en raison de la simplicité des calculs. Faire cette hypothèse de Kapp revient à supposer que le flux est forcé; comme elle n'est pas parfaitement exacte, en particulier aux faibles fréquences où les résistances deviennent prépondérantes devant les inductances, il ne faut pas s'étonner de trouver des écarts entre les grandeurs calculées par le modèle et les grandeurs mesurées en réalité.

Sur le modèle de la fig.5, il est alors possible de grouper les impédances primaires et secondaires; le rotor étant

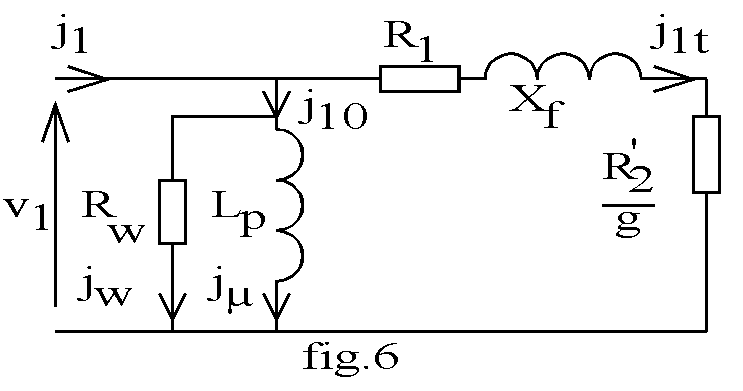
le plus souvent inaccessible à la mesure, nous donnons fig.6 le modèle obtenu en ramenant les impédances au primaire : R'₂ = R₂ / m^² est la résistance rotorique ramenée au stator et X_f est la réactance totale de fuites ramenée au stator; ce modèle est aussi appelé modèle à impédances groupées ou modèle en gamma.

3.1 Calcul en puissances complexes

En utilisant le modèle de la fig.4, nous allons exprimer la puissance complexe consommée par une phase

p₁ = p₁ + j.q₁ = V₁.J₁* ( le signe * marque le conjugué du nombre complexe).

En utilisant l'équation (1) du stator, il vient : p₁ = [(R₁ + j.X₁).J₁ +E₁] . J₁*; J₁. J₁* = J₁^² , carré de la valeur efficace; p_js = R₁.J₁^² représente les pertes par effet Joule dans une phase du stator et q_fuis = X₁.J₁^² représente la puissance réactive pour magnétiser le circuit de fuites du stator. Nous en déduisons : p₁ = E₁. J₁* + p_js + j.q_fuis .

L'équation des courants : J₁ = J₁₀ + J_1t = J_w + J_µ +J_1t donne :

E₁. J₁* = E₁.J_w* +E₁.J_µ* +E₁.J_1t* = R_w.J_w.J_w* +X_p.J_µ.J_µ* +E₁.J_1t* ; R_w modélisant les pertes dans le fer du stator et X_p la réactance de magnétisation, les deux premiers termes représentent les pertes dans le fer respectivement actives et réactives. Il vient donc : p₁ = (p_js +p_fers ) + j.( q_fuis + q_fers) +E₁. J_1t*

Le dernier terme p_em = E₁.J_1t* est la puissance complexe transmise au rotor appelée encore puissance électromagnétique. Le transformateur parfait transmettant intégralement la puissance, nous avons

p_em = E'₂.J'₂* = (R₂ /g + j.X₂).J'₂.J'₂* . J'₂.J'₂*= J₂^², carré de la valeur efficace du courant rotorique (par définition j₂ et j'₂ ont la même valeur efficace). p_jr = R₂.J₂^² représente les pertes par effet Joule dans une phase du rotor et

q_fuir = X₂.J₂^² représente la puissance réactive nécessaire pour magnétiser le circuit des fuites rotoriques. Il vient donc :

p_em = p_em + j q_em = p_jr / g + j.q_fuir .

La puissance électromagnétique active est égale au quotient des pertes par effet Joule au rotor par le glissement.

Cette relation est fondamentale pour l'étude du moteur asynchrone car dans les machines à rotor à cage elle représente le seul moyen de calculer les pertes par effet Joule au rotor dont on ne peut mesurer ni la résistance ni le courant.

La puissance active disponible pour entraîner le rotor est p_mot = p_em - pertes rotoriques; si nous négligeons les pertes dans le fer au rotor, il vient : p_mot = p_em - p_jr = (1 - g ).p_em. Pour obtenir la puissance utile, il suffit de retirer à cette puissance motrice les pertes mécaniques .

3.2 Bilan de puissance active

Si nous considérons les puissances pour les trois phases de la machine, il suffit de multiplier chacune des puissances calculées par 3. Nous obtenons alors le schéma ci-dessous

Le rotor tournant à la vitesse W = ( 1 - g) .W_s, le couple utile a pour moment T_u = P_u / W .

Le bilan peut être schématisé par la figure ci-contre :

Ce bilan de puissance appelle quelques remarques spécifiques à la machine asynchrone :

4.1 Séparation des pertes

Plusieurs méthodes peuvent être utilisées pour séparer les pertes mécaniques des pertes dans le fer.

Dans cet essai, le courant rotorique est nul ainsi que le couple; on doit entraîner la machine asynchrone par un moteur auxiliaire; on fournit électriquement au stator les pertes par effet Joule et les pertes dans le fer active et réactive : P_1syn = 3.V₁^² / R_w +3.R₁.J_1syn^² et Q_1syn = 3.V₁^² / X_p . Le moteur auxiliaire fournit les pertes mécaniques.

Esssai en moteur à vide

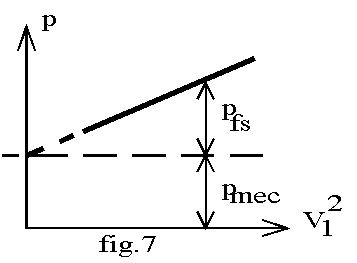
Pour séparer les pertes, il suffit de faire varier la tension au stator. Si la tension reste supérieure à 20 % environ de la tension nominale, la vitesse reste proche du synchronisme; les pertes mécaniques sont constantes et les pertes dans le fer varient proportionnellement au carré de la tension. Le graphe représentant p = P_1v - p_jsv en fonction de V₁^² est donc une droite. En extrapolant la droite à V₁ = 0, nous obtenons les pertes mécaniques.

Méthode des trois essais

Pour les machines à rotor bobiné, nous pouvons effectuer les trois essais suivants :

Dans cet essai, la puissance fournie au rotor se décompose en pertes par effet Joule que nous calculons, en pertes dans le fer stator et en pertes dans le fer du rotor. A l'arrêt, le champ stator tourne à la vitesse de synchronisme par rapport au rotor et induit des pertes p'_fr non négligeables. Nous en déduisons p' = p_fs + p'_fr .

Avec p' - p" = p_fs - p_mec et p =p_fs + p_mec , nous calculons p_fs = (p +p' -p") / 2 et p_mec = (p -p' +p") / 2

4.2 Obtention du modèle

L'essai à vide avec séparation des pertes permet de calculer R_w = 3.V₁^²/p_fs et X_p = 3.V₁^²/Q_vide.

Un essai en court-circuit rotor calé est identique à l'essai en court-circuit du transformateur. Nous devons réduire la tension stator pour limiter le courant à une valeur proche de la valeur nominale. Nous avons P_1cc =3.V₁^² / R_w +P_1t et Q_1cc =3.V₁^² / X_p + Q_1t . Nous pouvons en déduire P_1t = 3.R'₂.J_1t^², Q_1t = 3.X_f.J_1t^², et S_1t = 3.V_1cc.J_1t. Nous en déduisons J_1t , R'₂ et X_f. Le plus souvent les pertes dans le fer active et réactive peuvent être négligées et J_1t confondu avec J_1cc.

5 Calcul du moment du couple électromagnétique

Nous utilisons le schéma en gamma. Il vient :

En négligeant la résistance du stator devant la réactance de fuites et en multipliant numérateur et dénominateur par

g / R'₂, nous obtenons l'expression simplifiée du couple :

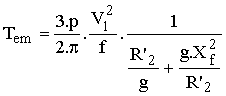
Lorsque le glissement varie, seul le dénominateur varie; ce dénominateur est la somme de deux termes dont le produit est constant; il est minimal, donc le couple est maximal, lorsque les deux termes sont égaux soit pour la valeur de g : g_max = R'₂ / X_f = R'₂ / 2.p.f.L_f.

La valeur maximale du couple est :

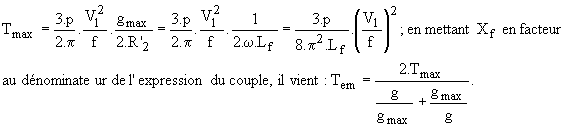
5.2 Influence de la résistance du stator

En reprenant l'expression du couple sans négliger la résistance R₁, il vient

T_em = (3.p.V₁^² / 2.p.f).y(g). Etudions la fonction y(g) = ( g / R'₂ ).[ (R₁ +R'₂ / g)^² + X_f^² ]; sa dérivée est dy / dg =(R₁^² +X_f^² ) /R'₂ -R'₂ / g^²; elle s'annule pour la valeur du glissement g'_max = R'₂ / (R₁^² +X_f^² ); pour cette valeur, le moment du couple est maximal avec T'_max = (3.p.V₁^² /2.p.f) / 2.[R₁ + Ö(R₁^² +X_f^² )].

5.3 Caractéristique mécanique

Pour une machine donnée alimentée par un réseau de tension et de fréquence fixe, le moment du couple ne dépend

que du glissement. Les relations ci-dessus permettent de tracer la caractéristique T_em (g) et en remplaçant g par

1-n/n_s la caractéristique mécanique T_em (n).

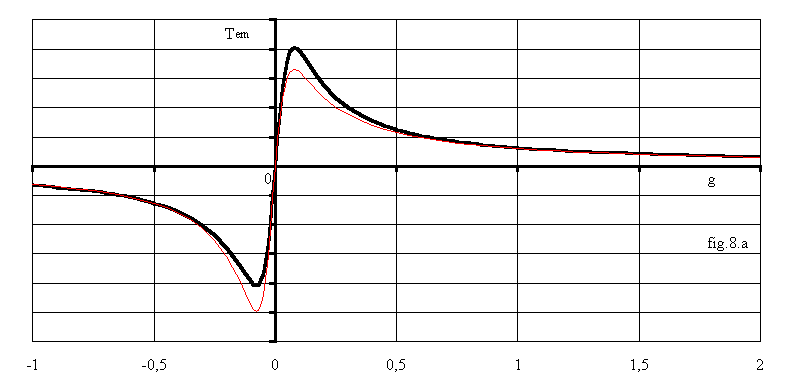
La fig.8.a montre que la courbe obtenue par la formule approchée est peu différente de celle obtenue en tenant compte de R₁ (graphe en trait fin rouge). Pour les faibles valeurs du glissement, g / g_max est très petit devant g_max / g et le couple est peu différent de 2.T_max.g / g_max = k.g; le graphe est donc linéaire au voisinage de g = 0. Pour les forts glissements g / g_max est très grand devant g_max / g et le couple est peu différent de 2.T_max.g_max / g = k' / g; le graphe est alors de forme hyperbolique.

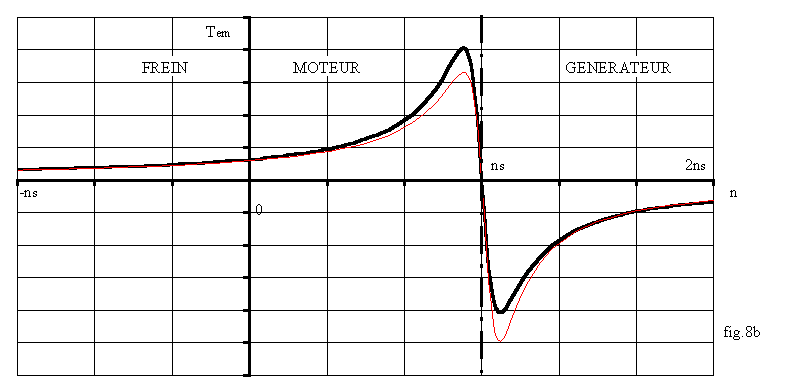
Sur la fig.8.b, on peut distinguer trois zones de fonctionnement; en négligeant les pertes autres que par effet Joule au rotor, nous avons T_u = T_em et P_u = T_em .2.p.n / 60 et P_a = P_u / (1- g)

è pour 0 < n < n_s soit 0 < g < 1, T_u est positif, n et 1- g sont positifs; les puissances utile et absorbée sont positives : la machine fonctionne en moteur

5.4 Stabilité du fonctionnement

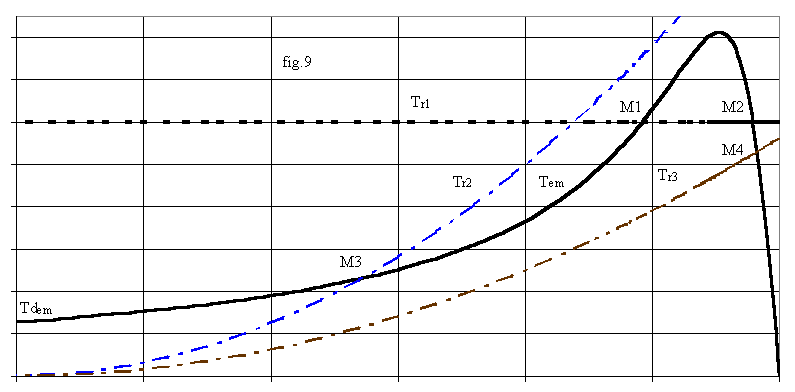
La charge imposant un couple résistant T_r(n), en régime permanent le point de fonctionnement est à au point d'intersection de la caractéristique mécanique avec celle de couple résistant.

v aucun point de fonctionnement si T_r > T_max

vun point de fonctionnement si T_r < T_dem ou si T_r = T_max

vdeux points de fonctionnements dans les autres cas ; pour un couple T_r1 la fig.9 donne les deux points possibles M1 avec un glissement g₁ > g_max et M2 avec un glissement g₂ < g_max .

Montrons que seul le point M2 est stable. En M1 une augmentation de la vitesse due à une cause quelconque déplace le point de fonctionnement vers la droite. Dans ce cas on a T_u > T_r; la relation fondamentale de la dynamique,

J.dW / dt = T_u - T_r montre que la dérivée est positive donc la vitesse croît. Une augmentation de vitesse fait augmenter encore plus la vitesse, il y a bien instabilité. De même une diminution de vitesse à partir de M1 créerait une dérivée négative; le moteur cale.

Au point M2 en revanche, une augmentation de la vitesse crée un couple moteur inférieur au couple résistant; la dérivée de la vitesse est négative; la vitesse diminue et on revient en M2 .

Le point de fonctionnement est stable si la dérivée par rapport à la vitesse du couple résistant est supérieure à celle du couple moteur. Pour les charges à couple constant ou faiblement variable avec la vitesse, seuls les points de fonctionnement correspondant à g < g_max sont stables.