Les bases de Windows XP

4 3

Électrotechnique

x x Module 4: x

"Machine asynchrone"

Chapitre 4.1

Principes

Choix : cliquez sur la flèche

Plaque signalétique

Modèle

Bilan de puissance

Caractéristique mécanique

Une machine asynchrone triphasée porte sur sa plaque signalétique : 230/400 V - 70/40 A - 50 Hz - 9 80 tr/min - 20 kW Le rotor bobiné à bagues est couplé en étoile On donne : la résistance d'une phase du stator R1= 120 mW la résistance d'une phase du rotor R2 = 200 mW les pertes mécaniques pmec = 800 W
1 Étude de la plaque signalétique
1.1 Quelle est la tension nominale par enroulement	La plus faible marquée sur la plaque donc 230V Réponse
1.2 Quel est le courant nominal par enroulement		Le plus faible marqué sur la plaque soit 40 A Réponse
1.3 Quel est le nombre de pôles de la machine ?	La vitesse de synchronisme ne peut être que 1000 tr/mn donc p = 3 ; la machine a 6 pôles Réponse
1.4 Que représente la puissance 20 kW ?	La puissance utile en moteur Réponse
1.5 Quel doit être le couplage sur un réseau 130/230 V ?	Vnom = Uréseau donc couplage triangle Réponse
2 Modèle équivalent
L'essai en moteur à vide, stator couplé en étoile, sous tension nominale donne : I10 = 15 A et P10 = 1,7 kW
2.1 En considérant que le glissement est négligeable, calculer les pertes fer stator	P10 = pjst+pfst+pmec Aide	pjst = 3.R1.J10² = 81 W pfst = 819 W Réponse
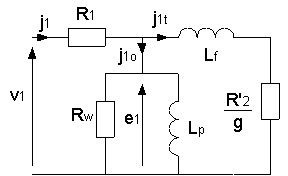
2.2 Calculer la f.é.m E1	Utiliser le théorème de Boucherot Attention : les pertes mécaniques ne sont pas modélisées sur le schéma A ide	une phase consomme : V10 = 400/Ö3=231 V ; J10 = 15 A ; s10 = 3464 VA q10 = Ö(s1o²-p1o²)=3417 VAR g = 0 donc J1t = 0 Rw consomme pfst/3 = 273 W ; Lp consomme q10 = qfst le circuit magnétique consomme sfer = Ö(pfst²+qfst²)=3428 VA E1 = sfer/J1o = 229 V Réponse
2.3 Calculer Rw et Lp		Rw = E1²/pfst = 192 W Xp =E1²/qfst = 15,3W ; Lp = 48,9 mH Réponse
L'essai en court-circuit rotor calé, stator couplé en étoile, donne : U1cc =104 V ; I1cc = 38 A et P1cc = 1,1 kW
2.4 Calculer E1 puis J1t	Utiliser la méthode de Boucherot, calculer p, q, s après R1, en déduire E1cc puis après le circuit magnétique, en déduite J1tcc Aide	V1cc = 60 V ; J1cc = 38 A ; p1cc = 367 W ; q1cc = 2250 VAR Après R1 : p'1cc = p1cc - R1.J1cc² = 193 W; q'1cc = q1cc ; s'1cc = 2260 VA ; E1cc = s'1cc/J1cc = 59,4 V pfst = E1cc²/Rw = 18 W ; qfst = E1cc²/Xp = 231 VAR Après le circuit magnétique : pem = p'1cc-pfst = 175 W; qem = q'1cc-qfst = 2019 VAR ; sem = 2027 VA ; J1tcc = sem/E1cc =34 A Réponse
2.5 Calculer Lf et R'2	n = 0 donc g = 1 pem = 3.R'2.J1tcc² donc R'2 = 0,15 W qem = 3.Xf.J1tcc² donc Xf = 1,74 W ; Lf = 5,53 mH Réponse
2.6 Calculer le rapport de transformation à l'arrêt de la machine		R'2 est la résistance R2 ramenée au primaire donc R'2=R2/m² d'où m = Ö(R2/R'2)=1,15 Réponse
3 Bilan de puissance au point nominal *On utilisera les données de la plaque signalétique et les résultats acquis ci-dessus*
3.1 Calculer la puissance motrice		Pmot = Pu + pmec = 20,8 kW Réponse
3.2 Calculer les pertes par effet Joule au rotor et le courant rotorique	Relation fondamentale de la machine asynchrone pjr = g.Pem Aide	g = (1000 -980)/1000 = 2 % Pmot = (1-g).Pem ; pjr = g.Pmot/(1-g) = 420 W pjr = 3.R2.J2² donc J2 = I2 = 26,5 A Réponse
3.3 Calculer la puissance électromagnétique		Pem = Pmot + Pjr = 21,22 kW Réponse
3.4 Calculer la puissance absorbée et le facteur de puissance stator		P1 = Pem + pfst +pjst pjst = 3.R1.J1² = 580 W ; P1 = 22,62 kW cos j1 = P1/ Ö3.U1.I1 = 0,816 AR Réponse
3.5 Calculer le rendement		h = Pu / P1 = 88,4 % Réponse
3.6 Calculer les moments des couples utile et électromagnétique		Tu = Pu / W = 195 Nm Tem = Pem / Ws = 203 Nm Réponse
4 Caractéristique mécanique *On néglige la résistance du stator pour le calcul du couple électromagnétique* *La machine est alimentée sous tension et fréquence nominale* *Le stator est couplé en triangle*
4.1 Calculer la valeur maximale Tmax du moment du couple électromagnétique et le glissement gmax correspondant		Voir les formules dans le cours Tmax = (3.p/8.p².Lf).(V1/f)² ; gmax = R'2/2.p.f.Lf p = 3 (6 pôles) ; Lf =5,53 mH; R'2 = 0,15 W ; V1 = 230 V Tmax = 436 Nm ; gmax = 8,63 % Réponse
4.2 Calculer le moment du couple pour une vitesse de 985 tr/min		g = 1,5 % T=2.Tmax/(g/gmax+gmax/g)=147 Nm Réponse
4.3 Pour le couple précédent, calculer le courant en ligne	Pem = 3.R'2.J1t²/g donne J1t utiliser le modèle et le théorème de Boucherot pour calculer E1 puis J1 Aide	Pem = Tem.Ws = 15,41 kW ; J1t = 22,7 A Qem = 3.Xf.J1t²; = 2,68 kVAR ; Sem = 15,64 kVA E1=Sem/3.J1t = 230 V pfst = 3.E1²/Rw = 827 W ; qfst = 3.E1²/Xp = 10,37 kVAR P = Pem+pfst = 16,24 kW ; Q = Qem+qfst = 13,05 kVAR S = 20,83 kVA ; J1 = S/3E1 = 30 A I1 = 52 A ; cos j1 = P/S = 0,78 AR Réponse
4.4 Calculer la vitesse pour un couple électromagnétique de moment Tem = 100 Nm	Résoudre l'équations g² -(2.Tmax.gmax/Tem).g +gmax² = 0 Aide	On a deux solutions : 74,3 % et 1 % Seuls les points tels que g < gmax sont stables donc g = 1 % et n = ns.(1-g) = 990 tr /min Réponse
4.5 Calculer le moment du couple au démarrage		Au démarrage g = 1 Tdem = 2.Tmax/(1/gmax+gmax) = 75 Nm Réponse
4.6 On ajoute au rotor un rhéostat triphasé de résistance Rh = 100 mW par phase. Calculer la vitesse pour un couple électromagnétique de moment Tem = 100 Nm	Le couple maximal ne change pas et gmax est multiplié par (R2+Rh)/R2 Aide	Tmax = 436 Nm ; gmax = 13,9 % g² -(2.Tmax.gmax/Tem).g +gmax² = 0 On a deux solutions : 120 % et 1,6 % Seul la deuxième valeur correspond à un fonctionnement moteur g = 1,6 % et n = ns.(1-g) = 984 tr /min Réponse