L'écriture de la série peut prendre deux formes:

Le terme de fréquence f est appelé harmonique de rang 1 ou fondamental; le terme de fréquence n.f est appelé harmonique de rang n ou en abrégé harmonique n.

1.2 Calcul des coefficients

Calcul du terme constant

nous calculons la valeur moyenne de y(t) : Y_o = Y_moy.

Calcul des termes An et Bn

_et

Calcul des coefficients de la deuxième forme

1.3        Influence des symétries de la fonction

Si une fonction présente des symétries, tous les termes de la série de Fourier doivent présenter les mêmes symétries. Tout terme n'ayant pas les mêmes symétries que la fonction doit s'annuler par annulation du coefficient A_n ou B_n.

Les symétries possibles sont :

Ø      fonction paire = symétrie par rapport à l'axe Oy; y(-t) = y(t);

tous les coefficients B_n sont nuls

Ø      fonction impaire = symétrie par rapport à l'origine O; y(-t) = -y(t);

tous les coefficients A_n sont nuls.

Ø      fonction alternative : symétrie par rapport au point (T/2; 0); y(t+T/2) = -y(t)

tous les harmoniques de rang pair sont nuls : A_2p = B_2p = 0.

Ø      fonction "redressée" : symétrie par rapport à l'axe t = T / 2 : y(t+T/2) = y(t);

tous les harmoniques de rang impair sont nuls : A_2p+1 = B_2p+1 = 0.

 

1.5 Caractéristiques du signal

Ø      La valeur efficace du signal en fonction de la valeur des harmoniques : .

Ø      L'amplitude de chaque harmonique peut être caractérisée par son rapport à celle du fondamental,

exprimé en %; le taux d'harmonique n est : TH_n = 100*Y_n / Y_o.

Ø      Le taux global d'harmonique ou taux de distorsion harmonique est en % :

Plus ce taux est grand, plus le signal s'écarte de la forme sinusoïdale pure.

Ø      le spectre du signal représente l'amplitude des harmoniques en fonction du rang.

2 Puissances électriques

2.1 Cas général

On étudie un dipôle alimenté par un signal non sinusoïdal. Tension et courant sont des grandeurs non sinusoïdales de même fréquence:

2.2 Cas d'une tension sinusoïdale

On rencontre souvent le cas où un dipôle non linéaire est alimenté par une tension purement sinusoïdale. Dans ce cas, la tension ne comporte pas d'harmoniques alors que le courant déformé par la charge en comporte.

Expression des puissances

On appelle puissance déformante D, la quantité : ; c

ette puissance s'exprime en VA comme la puissance apparente.

Elle est nulle en régime purement sinusoïdal et augmente avec la déformation du courant, d'où son nom.

Le facteur de puissance peut s'écrire :

La valeur du facteur de puissance résulte donc de deux phénomènes :

v     la distorsion harmonique rendant I₁ / I < 1

v     la consommation d'énergie réactive, correspondant au terme cosj₁ appelé

déplacement du facteur de puissance, car il est dû au déphasage courant fondamental - tension.

Exemple

Soit un redresseur PD2 mixte alimentant une charge suffisamment inductive pour assurer un filtrage parfait du courant (fig.5a).

 

 

 

 

Les formes d'onde sont données par la fig.5b pour un retard à l'amorçage a des thyristors.

Le réseau fournit la tension v=V.Ö2.sinq. = 8,16 A ; J1 = 7,8 A ; cos j1 = 0,866

P = 1 553 W ; Q = 897 VAR ; S = 1 878 VA;

Le facteur de puissance est Fp = 0,827 inférieur de 4,5 % au facteur de déplacement.

Le taux global d'harmoniques du courant j est de 31,1 % et la puissance déformante D =  557 VA.

 

3 Effets polluants d'une charge non linéaire  

3.1 Effets sur la tension

Principe

Une charge non linéaire ou polluante est un récepteur qui alimenté par une tension sinusoïdale absorbe un courant alternatif non sinusoïdal. C'est par exemple le redresseur étudié au paragraphe 2.2.2.

On peut schématiser le fonctionnement d'un réseau alimentant une charge polluante par le modèle équivalent de la fig.6:

Le réseau fournit en tête de ligne la tension sinusoïdale v de fréquence f. La ligne est modélisée par une résistance en série avec une inductance. La charge est modélisée par des générateurs de courants en parallèle, chaque générateur correspondant à un harmonique du courant absorbé i.

Pour calculer la tension v' en bout de ligne, nous utilisons le théorème de superposition. A chaque étape du calcul, nous ne gardons que les générateurs de même fréquence n.f et les éléments passifs.

Nous constatons que chaque courant harmonique de la charge crée un harmonique proportionnel de tension. La tension en bout de ligne comportera donc des harmoniques de même rang que ceux du courant.

Exemple

Soit une salle informatique comportant 20 ordinateurs connectés en parallèle sur une ligne.

Les alimentations continues des boîtiers et des écrans forment une charge polluante.

L'analyse harmonique du courant consommé par la salle donne les résultats suivants:

La valeur efficace du courant est : I = 13,8 A et le taux global d'harmoniques THD = 130 %.

Pour une alimentation sous V = 230 V, les puissances consommées en négligeant les harmoniques de la tension sont : P = 1 670 W ; Q = 966 VAR ; S = 3 170 VA et D = 2 515 VA. Le facteur de puissance est F_p = 0,55. Le déplacement du facteur de puissance est cosj1 = cos[arctg(Q/P)] = 0,87.

Le réseau alimentant la charge a une puissance de court-circuit S_cc= 100 kVA; le courant de court-circuit est I_cc = 435 A; à f = 50 Hz, l'impédance de la ligne est donc Z_cc = 0,529 W. Si on estime à 10 le rapport entre partie imaginaire / partie réelle, j_cc = arg Z_cc = 84,3 °; la ligne peut donc être modélisée par une résistance R_cc = 53 mW en série avec une inductance L_cc = 1,68 mH.

Calculons les harmoniques de la tension v' côté salle informatique de la ligne :

       

Nous constatons que la tension v' est déformée par des harmoniques; son taux global d'harmoniques est égal à 13 %.

La fig.7 donne l'allure des grandeurs

3.2 Inconvénients des harmoniques

Ø      La présence d'harmoniques détériore le facteur de puissance donc, pour une tension et une puissance données, augmente le courant en ligne.

Ø      Les harmoniques du courant donnent à celui-ci un facteur de crête F_c = I_max/I_eff élevé; dans l'exemple traité au paragraphe 3.1.2, F_c = 44 /13,2 = 3,33 au lieu de 1,4 en régime sinusoïdal. Ces pointes de courant peuvent causer le déclenchement intempestif des disjoncteurs du circuit.

Ø      En distribution triphasé, les harmoniques peuvent créer un fort courant dans le conducteur de neutre même pour un récepteur équilibré. Ce courant est dû aux harmoniques de rang multiple de 3. En régime équilibré, les harmoniques n des trois courants de ligne sont déphasés de n*120°.

Ø      La déformation de la tension crée des perturbations dans le fonctionnement des équipements placés au voisinage de la charge polluante. Dans les machines électriques, les harmoniques de tension augmentent les pertes magnétiques. Dans les machines triphasées, l'analyse des déphasages faite ci-dessus montre que les harmoniques 1, 7, 13, … créent des champs tournants directs, les harmoniques multiples de 3 ne créent pas de champ tournant car ils sont en phase et les harmoniques 5, 11, 17… créent des champs tournants inverses donc des couples résistants. Les harmoniques perturbent le couple moteur et créent des vibrations mécaniques dues aux champs tournants de vitesse élevée.

Ø      Les condensateurs sont des composants particulièrement sensibles aux harmoniques puisque le courant croît inversement proportionnellement à la fréquence. La présence d'harmoniques peut créer un échauffement excessif et un vieillissement accéléré.

Ø      On utilise souvent des condensateurs en parallèle pour améliorer le facteur de puissance de l'installation; l'inductance de ligne peut créer avec ces condensateurs un circuit résonnant accordé sur la fréquence n.f d'un harmonique. L'impédance devient alors très faible à cette fréquence et il circule un courant harmonique i_n de valeur très élevée.

Reprenons les données de l'exemple ci-dessus. Pour compenser la puissance réactive, il faut un condensateur de capacité C = Q / w.V² = 58 µF. Utilisons un condensateur C = 50 µF.

Avec L = 1,68 mH, la fréquence de résonance est 549 Hz, fréquence voisine de celle de l'harmonique 11. On obtient les grandeurs de la fig.8:

On constate que la tension et le courant augmentent de façon dangereuse. Le courant efficace est multiplié par 3,6 alors qu'il devrait diminuer !

 

4 solutions à apporter

4.1 Normes

Afin d'éviter une pollution excessive des réseaux, une norme définit les limites à ne pas dépasser pour les harmoniques. Par exemple la norme CEI 61000-3-2 définit les valeurs harmoniques à ne pas dépasser pour les appareils électriques consommant moins de 16 A par phase :

 

 

4.2 Limitation de l'effet des charges polluantes

Ø      Un récepteur raccordé sur la ligne à proximité de la charge polluante sera alimenté sous une tension déformée. Pour limiter les effets de la charge polluante, il vaut mieux connecter le récepteur en tête de ligne.

Ø      On peut limiter la transmission des harmoniques en plaçant un inductance en série avec la charge polluante et en raccordant les autres récepteur en amont de cette inductance.

4.3 Filtrage passif

On peut piéger les harmoniques du courant en plaçant en parallèle avec la charge un circuit résonnant série R_F - L_F - C_F accordé sur la fréquence n.f de l'harmonique à atténuer. Ce circuit présente une impédance faible à la fréquence n.f et donc constitue un court-circuit pour le courant harmonique i_n; on évite ainsi la propagation dans la ligne. Aux autres  fréquences, l'impédance est élevée et modifie peu le comportement du circuit.

Reprenons l'exemple de la salle informatique et utilisons un filtre accordé sur la fréquence 150 Hz de l'harmonique 3. Nous gardons C = 50 µF pour compenser la puissance réactive; nous en déduisons

L =22,5 mH et nous prenons R = 0,1 ohm.

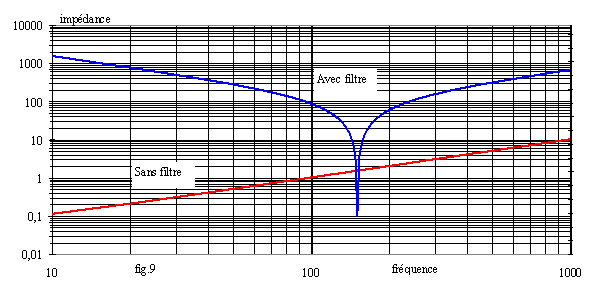
La fig.9 donne l'allure du module de l'impédance vue de la charge; sans filtre, cette impédance est celle de la ligne Z_L = R+j.L.w. L'impédance du filtre est Z_F = R_F+j(L_F.w-1/C_F.w). L'impédance vue de la charge est équivalente à Z_L et Z_F en parallèle.

L'analyse du réseau donne les harmoniques de la fig.10 (pour la tension en bout de ligne, on n'a pas représenté le fondamental car les harmoniques sont faibles et l'échelle à utiliser ne permettrait pas la visualisation précise des harmoniques) : en rouge plein on donne les valeurs sans filtre et en hachuré bleu, les valeurs avec filtre.

On constate pour le courant en ligne, un réduction de 94 % de l'harmonique 3 et de 7 à 10 % pour les autres harmoniques.

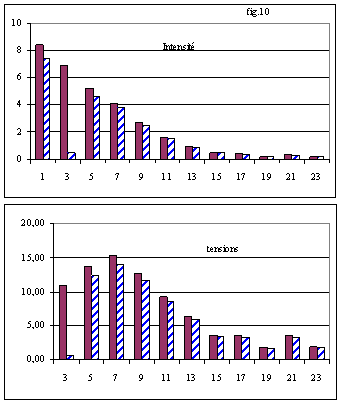
On retrouve des résultats similaires pour la tension v'.

Le taux global d'harmoniques passe de 121 à 92 % pour le courant et de 47 à 11 % pour la tension.

Les puissances consommées sont : P = 1 691 W , Q = 0,6 VAR. Le facteur de forme passe de 0,55 à 0,74.

La fig.11 donne l'allure des grandeurs.

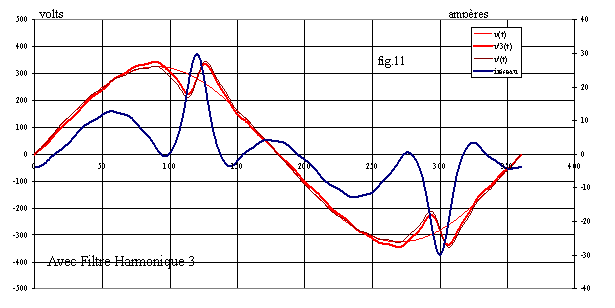
Sur ces graphes, on ne peut constater une amélioration sensible des formes d'ondes car le signal reste riche en harmoniques.

On peut encore améliorer le fonctionnement en plaçant en parallèle des filtres accordés sur les harmoniques 3, 5, 7, …Pour choisir les composants, on partage la capacité nécessaire pour compenser la puissance réactive entre les trois filtres inversement proportionnellement à la fréquence; on en déduit la valeur des trois inductances.

 

 

 

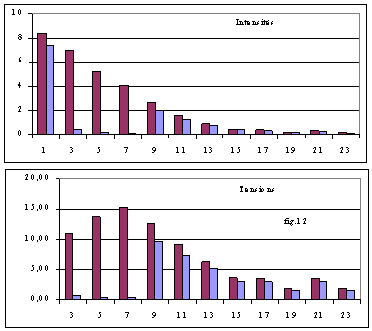
La fig.12 donne les spectres du courant réseau et de la tension v' en bout de ligne avec trois filtres accordés sur les harmoniques 3, 5 et 7 avec les valeurs du tableau ci-dessus.

La fig.13 donne l'allure du courant en ligne et de la tension en bout de ligne.

On observe encore un courant loin d'une forme sinusoïdale; en revanche, la forme de tension s'est améliorée.

Cette étude montre la difficulté de respecter la norme lorsque le signal est riche en harmoniques.

Il faudrait rajouter des filtres accordés sur les rangs 9, 11, 13 pour rester dans la norme ce qui donne un minimum de six filtres donc un montage complexe et cher.

Cette méthode de filtrage passif pourra s'appliquer lorsque il y a peu d'harmoniques importants de rang faible.

4.4 Filtrage actif

Le principe du filtrage actif est de mesurer la différence i_h = i - i₁ entre le courant en ligne pollué et sa composante fondamentale puis de générer par un convertisseur, un courant - i_h que l'on réinjecte dans la ligne. On annule ainsi tous les courants polluants.

Le synoptique d'un tel montage est donné fig.14 :

On prélève le courant charge et on retire sa composante fondamentale par un filtre réjecteur.

Le signal i_h pilote un onduleur de courant asservi de façon à générer le courant opposé.

L'onduleur doit être alimenté en continue. Cette tension est créée par un redresseur et un hacheur élévateur piloté de façon à absorber un courant sinusoïdal : un simple redresseur suivi d'un filtre par condensateur générerait des harmoniques supplémentaires !

4.5 Conclusion

Cette étude montre :

Ø      l'importance des problèmes de distribution créés par les harmoniques et leurs inconvénients sur le fonctionnement des équipements.

Ø      la difficulté d'éliminer les harmoniques pour respecter les normes : montages complexes et coûteux

On peut en conclure qu'il vaut mieux essayer de ne pas générer des harmoniques plutôt que de tenter de les éliminer.

Les principales sources d'harmoniques sont :

Ø      les alimentations continues avec redresseur et filtrage par condensateur pour alimenter des équipements tels que les ordinateurs ou des onduleurs.

Ø      les gradateurs de conversion alternative - alternative pour alimenter des systèmes d'éclairage ou des machines asynchrones.

Dans le premier cas, on peut remplacer le redresseur et le filtre par un ensemble redresseur - hacheur élévateur piloté pour absorber un courant quasi sinusoïdal ( système PFC ou PMFC).

Dans le deuxième cas, on peut rechercher des structures et des modes de commande limitant la génération d'harmoniques.