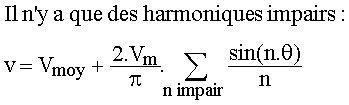Les bases de Windows XP

4 3

Électrotechnique

x x x

Module 7

Chapitre 7.1

CEM conduite

Choix : cliquez sur la flèche

Tension et courant déformés

Tension sinusoïdale et courant déformé

Pour le calcul des harmoniques, on pourra consulter la table obtenue en cliquant ici

Exercice 1 On considère un dipôle monophasé dont on donne ci-dessous la tension et le courant avec Vm = 200 V et Im = 10 A
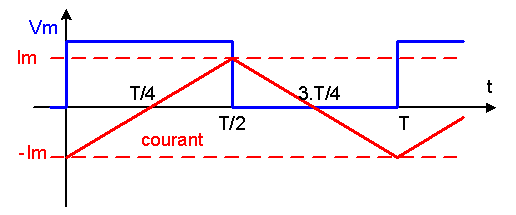
1 Étude de la tension
1.1 Calculer les valeurs moyenne et efficace de la tension	Vmoy = Vm/2 = 100 V Veff = Vm/Ö2 = 141,4 V Réponse
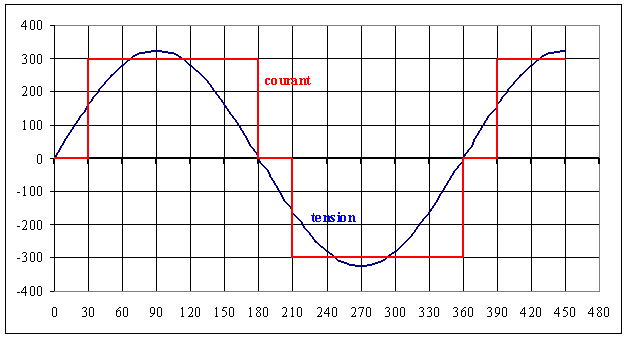
1.2 Décomposer la tension en série de Fourier jusqu'au rang 10	Utiliser la fonction rectangulaire du tableau avec YM = Vm, Ym = 0 et a = 1/2 Aide	Réponse
1.3 Calculer le taux global d'harmoniques		THD = 42,9 % Réponse
2 Étude de l'intensité
2.1 Calculer les valeurs moyenne et efficace de l'intensité	i est alternative donc Imoy = 0 Ieff = Vm/Ö3 = 57,7 A Réponse
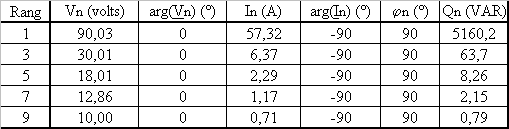
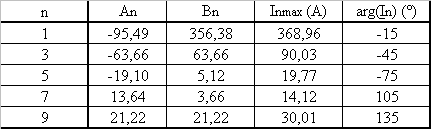
2.2 Décomposer l'intensité en série de Fourier jusqu'au rang 10	Utiliser la fonction triangulaire du tableau avec YM = Im, Ym = - Im et a = 1/2 Aide	Fonction alternative donc que des harmoniques impairs pour n impair Inmax = 2.Im/p².n² i = 81,1.cos(w.t-180) +9,01*cos(3.w.t-180)+3,24.cos(5.w.t-180) +1,65.cos(7.w.t-180)+1.cos(9.w.t.-180) Réponse
2.3 Calculer le taux global d'harmoniques		THD = 12,1 % Réponse
3 Étude des puissances . On se limitera au rang 10
3.1 Calculer la puissance active	P = S(Vn.In.cos jn) Comme il y un déphasage de 90° entre cosq et sin q on a P = 0 Réponse
3.2 Calculer la puissance réactive	Q = S(Vn.In.sin jn)/n = 5 235 VAR Comme il y un déphasage de 90° entre cosq et sin q Réponse
3.3 Calculer la puissance apparente	*S = V. I =141,4 57,7 = 8159 VA** Réponse
Exercice 2 Un réseau sinusoïdal monophasé de tension efficace V = 230 V et de fréquence f = 50 Hz alimente par une ligne une charge consommant l'intensité ci-dessous :
1 Étude de l'intensité
1.1 Calculer les valeurs moyenne et efficace de l'intensité	Fonction alternative donc Imoy = 0 Ieff = Im/Ö(150/180) = 274 A Réponse
1.2 Décomposer l'intensité en série de Fourier jusqu'au rang 10	Utiliser la fonction créneau décalé du tableau avec YM = Im, Ym = - Im a = p/6 et b = p Aide	Fonction alternative donc il n'y a que des harmoniques impairs Réponse
1.3 Calculer le taux global d'harmoniques	THD = 25,6 % Réponse
2 Étude des puissances On néglige l'impédance de la ligne
2.1 Calculer les puissances active et réactive	Seul le fondamental du courant compte : P = V.I1.cos j1 = 58 kW Q = V.I1.sinj1 =15,5 kVAR avec I1 = 369/Ö2 = 261 A et j1 = argV-argI1 = 15° Réponse
2.2 Calculer le facteur de puissance	Fp = P / S = 0,92 *avec S = V.I = 230 274 = 63 kVA** Réponse
2.3 Calculer le déplacement du facteur de puissance	DPF = cos j1 = 0,966 Réponse
2.4 Calculer la puissance déformante	D = Ö(S² - P² - Q²) = 19,1 kVA Réponse
2.5 Calculer la capacité du condensateur qui compense la puissance réactive de la charge	La charge consomme Q = 15,5 kVAR Qc = -Q = -C.w.V² donc C = 933 µF Réponse
2.6 Le facteur de puissance avec le condensateur est-il égal à 1 ?	Non car le courant est toujours déformé donc il y a toujours de la puissance déformante Réponse
3 Déformation de la tension La tension en tête de ligne est sinusoïdale de valeur efficace V = 230 V et la ligne est modélisée par une résistance R = 50 mW en série avec une inductance L = 0,4 mH
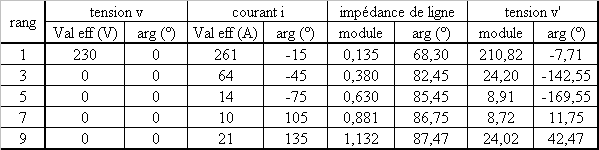
3.1 Calculer les harmoniques de la tension en bout de ligne (côté charge)	Appliquer le théorème de superposition en gardant dans chaque état un seul harmonique de v et de i Aide	V'n = Vn - Zn.In avec Zn = R+j.n.L.w Réponse
3.2 Calculer le taux global d'harmoniques de la tension en bout de ligne	THD = 25,2 % Réponse
3.3 Si on branche le condensateur du 2.5, y-a-t-il un risque de résonance ?	La fréquence de résonance avec l'inductance de ligne est f = 1/2.p.Ö(L.C) = 260 Hz Cette fréquence est proche de celle de l'harmonique 5 donc le risque de renforcer cet harmonique existe Réponse
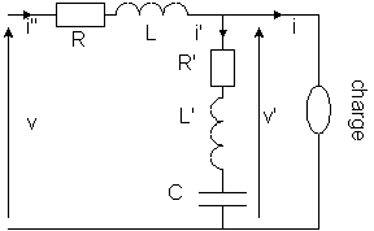
4 Filtrage des harmoniques On étudie le réseau avec filtre modélisé ci-dessous :
4.1 Pour C = 933 µF, calculer L' pour accorder le filtre sur l'harmonique 3; calculer R' pour que la bobine ait un facteur de qualité Qo = 10 à la résonance	A la fréquence f' =150 Hz, il vient L' = 1/C.w'² = 1,21 mH Qo = L.w'/R' donc R' = 110 mW Réponse
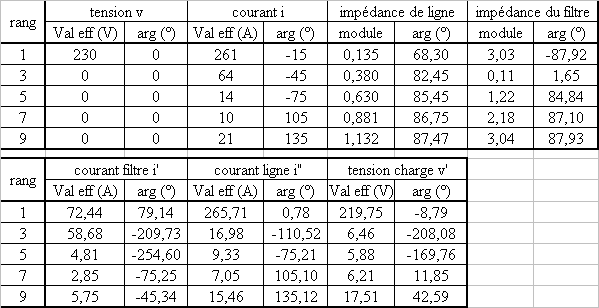
4.2 Calculer les harmoniques de i', i" et v'	Appliquer le théorème de superposition en gardant dans chaque état un seul harmonique de v et de i Écrire les équations en complexe Aide	Vn = Zn.I"n +Z'n.I'n ; I"n =I'n + In ; V'n = Z'n.I'n Zn = R+j.n.L.w et Z'n = R'+j.(n.L'w-1/n.C.w) I'n = (Vn-Zn.In)/(Zn + Z'n) Réponse
4.3 Calculer les taux globaux d'harmoniques de i" et v'. Que peut-on en conclure ?	THDi" = 9,7 % et THDv' = 9,3 % Le taux d'harmoniques de i" a diminué de 62 % et celui de v' de 63 % Cela correspond à la diminution des harmoniques en particulier l'harmonique 3 qui est divisé à peu près par 10 Réponse
4.4 Calculer les puissances active, réactive, apparente et déformante en tête de ligne	P = V.I"1.cos j"1 = 61,1 kW Q = V.I"1.sinj"1 =-0,83 kVAR avec I"1 = 266 A et j"1 = argV-argI"1 = -0,78 ° S = V.I" = 61,4 kVA avec I" = Ö(I"n²) = 267 A D = 5,93 kVA Réponse
4.5 Calculer le facteur de puissance et le déplacement du facteur de puissance en tête de ligne	Fp = P / S = 0,995 DPF = cos(-0,78°) =0,99991 AV Réponse