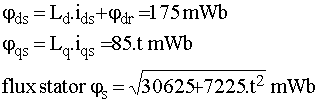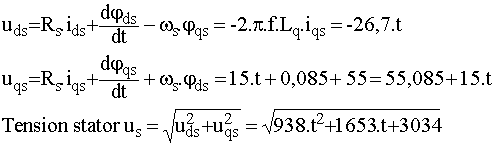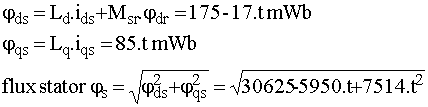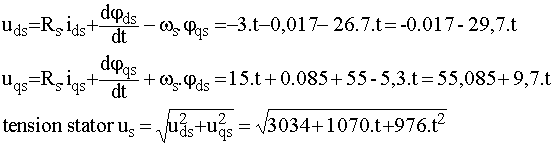Électrotechnique
Module 7 :
"Modèles avancés"
|
Chapitre 7.2
Commandes avancées
|
1 Commande à ids = 0 : on applique un courant iqs = 10.t |
||
1.1 Comment doit-on adapter les équations de la machine dans le cas d'un rotor à aimants permanents |
Dans les équations du cours, le flux rotor d'axe d s'écrit Msr.ir, nous remplaçons cette expression par jr |
|
1.2 Donner l'expression du couple en fonction du temps |
Tsy = (3.p/2).jr .iqs p = 2 paires de pôles donc Tsy = 5,25.t Trel = (3.p/2).(Ld-Lq).ids.iqs = 0 Tem = Tsy + Trel = 5,25.t
|
|
1.3 Donner l'expression de la valeur efficace du flux stator |
|
|
1.4 Donner les expressions des tensions stator uds et uqs en fonction du temps; en déduire l'expression de la valeur efficace de la tension stator |
|
|
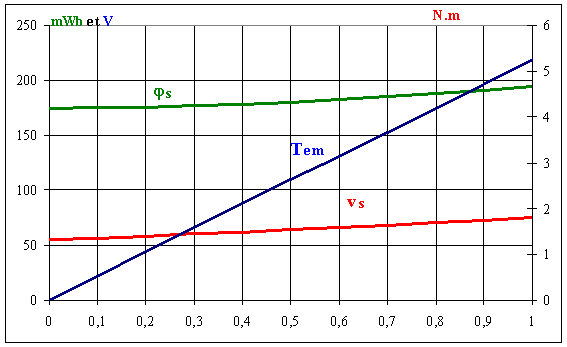
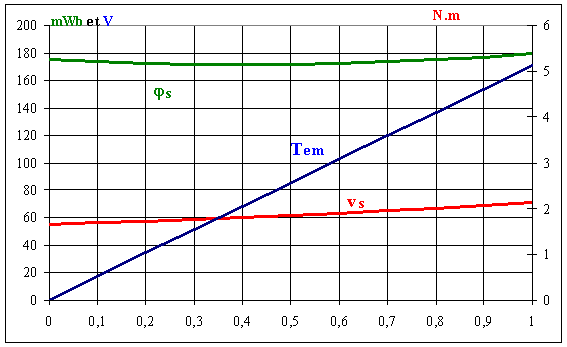
1.5 Représenter les graphes du couple, du flux et de la tension stator en fonction du temps variant de 0 à 1 seconde. |
Tsy = (3.p/2).jr .iqs = 5,25.t Trel = (3.p/2).(Ld-Lq).ids.iqs = -0,12.t Tem = Tsy + Trel = 5,13.t
|
|
2 on applique les courants ids = -2.t et iqs = 10.t |
||
2.1 Donner l'expression du couple en fonction du temps |
|
|
2.2 Donner l'expression de la valeur efficace du flux stator |
|
|
2.3 Donner l'expression de la valeur efficace de la tension stator |
|
|
2.4 Représenter les graphes du couple, du flux et de la tension stator en fonction du temps variant de 0 à 1 seconde. |
g = (1500 - 1448)/1500 = 0,13 % ; on en déduit que le courant rotorique est négligeable ; si on confond E et Vs, Ps = 3.Rs.Js² + 3.Vs² /Rw + pmec pjs = 68,4 W ; pfer = 109,3 W On en déduit les pertes mécaniques : pmec = 32,3 W |
|
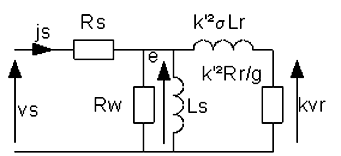
1.1 On réalise un essai au synchronisme, stator couplé en triangle sous tension nominale. On mesure Is = 3,7 A et Ps = 170 W. Montrer que l'on peut en déduire Rw et Ls. |
|
|
1.2 On réalise un essai en moteur à vide, stator couplé en triangle sous tension nominale. On mesure la vitesse n = 1 498 tr/min et Is = 3,9 A , Ps = 210 W. Que peut-on en déduire ? |
J.dW/dt = Tu - Tr = Tem -Tp -Tr A vide Tr = 0 , l'alimentation étant coupée Tem = 0 donc J.dW/dt = -Tr Tr est le couple dû aux pertes mécaniques Le ralentissement étant linéaire, le couple de pertes est constant; de la question 1.2, on déduit Tr = pmec /W = 32,3/(p. 1498/30) = 0,17 Nm dW/dt = (p/30).(dn/dt) = -7,85 rd/s² d'où J = 0,022 kg.m² En 120 ms, la vitesse a diminué de 75*0.12/60 = 0,15 tr/min; on peut donc considérer qu'elle reste constante
|
|
1.3 On effectue un essai en moteur en charge, stator couplé en étoile sous tension nominale. On mesure Is = 3,4 A, Ps = 1 780 W et n = 1 450 tr/min Montrer que l'on peut en déduire R' = k'².R r et L'r = k'². s .L r |
Le courant stator étant nul, le champ stator est nul; la f.é.m. du stator ne peut-on être due qu'au champ du rotor donc au courant rotor; le rotor étant en court-circuit, ce courant décroît avec la constante de temps tr = Lr /Rr . |
|
1.4 La machine fonctionnant à vide sous tension nominale, on coupe l'alimentation et on observe que la vitesse diminue linéairement avec une pente de -75 tr/min par seconde. Montrer que l'on peut en déduire le moment d'inertie J de la machine. |
v = e = Vmax.exp(-t/tr).cos w.t. On en déduit : exp(-10.T/ tr) = 0,26 donc tr = 148 ms
|
|
Cliquez ici pour voir la figure us(t)
|
||
1.5 Que peut-on dire de la vitesse durant le relevé de us(t)? |
L'r / R' = k'². s.Lr / k'².Rr = s . tr d'où s = 0,1 s = 1-M²/(Ls.Lr) = 1 - k donc k = 1 – s = 0,9
|
|
1.6 Montrer que la tension us décroit avec la constante de temps rotorique tr = Lr /Rr |
Réponse |
|
1.7 Sachant qu'à la 10 ème période après la coupure, l'amplitude est passée de 100% à 26 %, en déduire tr. |
Réponse |
|
1.8 En déduire la valeur de s et de k = M²/(Lr.Ls) |
Réponse |
|