1 généralités

Un circuit magnétique est un ensemble de matériaux assemblés pour former un ou plusieurs chemins fermés pour la circulation du champ magnétique. Ce champ est créé par un ou plusieurs bobinages portés par des portions du circuit appelées noyaux. Les noyaux sont reliés par des culasses.

Nous étudions des circuits de forte perméabilité relative et de géométrie telle que le champ soit canalisé à l'intérieur du circuit, ce qui veut dire que le champ magnétique est considéré comme nul à l'extérieur du circuit magnétique. Nous supposons de plus que B et H sont normaux à la section droite de toute portion du circuit et ont un module constant sur toute la surface de cette section.

2 circuit magnétique linéaire

Nous étudions dans ce paragraphe des circuits magnétiques formés de matériaux linéaires c'est à dire de perméabilité µ indépendante de l'excitation. Ces circuits ont peu d'intérêt en pratique en raison de la faible valeur de µ mais leur étude permet une première approche simple de l'étude

2.1 Circuit magnétique homogène

Nous disons qu'un circuit magnétique est homogène s'il est formé d'un seul matériau de section constante et qu'il offre un seul circuit fermé pour la circulation du champ

Appliquons le théorème d'Ampère au contour G formé par la ligne de champ moyenne orientée dans le sens direct. La circulation de l'excitation de direction parallèle à ce contour de longueur l est H.l ; elle est égale à la somme des courants enlacés. La bobine de n spires crée un champ de sens opposé à G et la bobine de n' spires crée un champ dans le sens de G, nous aurons donc H.l = n'.I' - n.I. Le champ magnétique est B = µ.H et le flux à travers la section droite est F = B.S ; nous en déduisons :

F = µ.S.( n'.I' - n.I) /l.

De manière générale, nous appelons

force magnétomotrice (en abrégé f.m.m.) la somme des courants enlacés; pour chaque bobine de n_i spires parcourue par le courant d'intensité I_i ,la f.m.m. est e_i.n_i.I_i , avec e_i = +1 si la bobine crée un champ dans le sens de parcours de G et e_i = -1 si la bobine crée un champ dans le sens opposé au sens de parcours de G .

réluctance du circuit la quantité R =l / µ.S exprimée en inverse d'henry (H^-1)

loi d'Hopkison la relation entre le flux et la f.m.m. : E = R .F .

2.2 Différence de potentiel magnétique

Soit un noyau de longueur l, de section S et de perméabilité µ, portant un bobinage de n spires parcourues par le courant d'intensité I.

Par analogie avec les circuits électriques, créons un modèle pour ce noyau. La grandeur qui circule dans le noyau est le flux analogue au courant électrique. Orientons arbitrairement le flux (fig.2). La bobine est modélisée par sa f.m.m. E = n..I orientée dans le sens du champ créé par ce bobinage (règle du tire-bouchon ou du bonhomme d'Ampère); cette f.m.m. se représente comme une f.é.m. électrique. Le matériau magnétique est caractérisé par sa réluctance R =l / µ.S représentée comme une résistance électrique R. La différence de potentiel magnétique (d.d.p.m. en abrégé) se calcule comme la d.d.p. électrique V = ± E ± R I par : V = ± E ± R F ; on prend le signe + pour E si elle est orientée dans le sens de V, - dans le cas contraire; comme en électricité on prend le signe +R.F si V est de sens opposé à F et - R.F dans le cas contraire; par exemple pour la fig.2, nous écrivons : V = E + R.F = H.l

2.3 Association en série de tronçons homogènes

Nous étudions le cas ou le circuit magnétique est composé de plusieurs tronçons homogènes associés de façon à créer un seul chemin de circulation du flux

Chaque tronçon T_i est caractérisé par sa longueur moyenne l _i , sa section S_i et sa perméabilité µ_i. La conservation du flux impose B_i.S_i = Cste.

Pour l'exemple de la fig.3, la circulation de l'excitation est : H₁.l₁+ H₂.l ₂+ H₃.l ₃ = n₁.I₁-n₂.I₂= E , f.m.m. totale.

Nous avons: H_i = B_i / µ_i = F_i / µ_i.S_i ; d'où H_i. l _i = F_i.( l _i / µ_i.S_i ) ; R_i = l _i / µ_i.S_i est la réluctance du tronçon T_i.

Il vient donc F.(R₁+ R₂ + R₃) = E.

Les réluctances des tronçons placés en série s'ajoutent comme les résistances dont elles sont l'analogue dans les circuits magnétiques.

Si nous modélisons chaque tronçon par le modèle équivalent décrit au paragraphe précédent et en comptant les d.d.p.m en sens inverse du contour G, nous avons : V₁ = -n₁.I₁ + R₁.F ; V₂ = n₂.I₂ + R₂.F et V₃ = R₃.F ; l'équation du théorème d' Ampère peut aussi s'écrire : V₁ + V₂ +V₃ = 0, équation analogue à la loi des mailles en électricité.

2.4 Association en parallèle de tronçons homogènes

Soit deux tronçons T₂ et T₃ en parallèle, c'est à dire deux tronçons offrant deux chemins différents pour le flux à partir du tronçon T₁.

Le flux F₁ dans T₁ se divise en deux flux tout en se conservant: F₁ = F₂ + F₃ . La d.d.p. magnétique V est la même pour les deux tronçons : V = H₂.l ₂ = H₃.l ₃ ou V = R₂.F₂ = R₃.F₃.

Nous en déduisons : F = V .( 1/R₂ +1/R₃ ) . Les deux tronçons en parallèle sont donc équivalents à un seul tronçon de réluctance R telle que : 1/R = 1/R₂ +1/R₃ . Nous obtenons une loi d'association analogue à celle des résistances en parallèle.

Pour les flux la loi de conservation est analogue à la loi des nœuds en électricité.

2.5 Exemple de calcul

Soit le circuit magnétique de la fig.5; on donne:

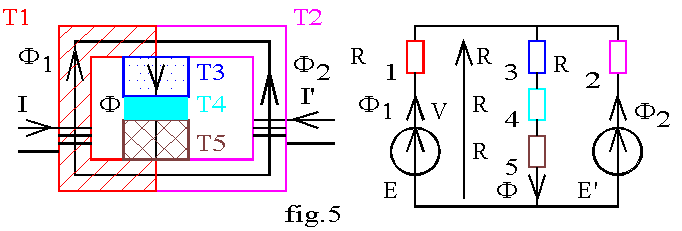
tronçon T₁: longueur l₁ = 80cm ; section S₁=10cm^² ; perméabilité relative µ_r1 =1 000;

tronçonT₂ : longueur l₂ =110cm ; section S₂= 10cm^² ; perméabilité relative µ_r2 =1 500;

tronçon T₃: longueur l₃ = 15cm ; section S₃ =12cm^² ; perméabilité relative µ_r3 = 800;

tronçonT₄ : longueur l₄ = 1mm ; section S₄=12cm^² ; perméabilité relative µ_r4 = 1 (air);

tronçon T₅: identique au tronçon T₃.

La bobine du noyau T₁ comporte n = 1 000 spires parcourues par un courant continu d'intensité I. La bobine du noyau T₂ comporte n' = 800 spires parcourues par un courant continu d'intensité I' = 2 A.

Nous voulons calculer l'intensité I pour avoir un champ magnétique B = 1T dans l'air du tronçon T4.

Le flux F commun aux tronçons T₃, T₄, T₅ placés en série est F =B.S₄ = 1,2 mWb.

Calculons les réluctances des cinq tronçons en utilisant R_i = l_i /(µ_o.µ_ri.S_i ):

Tronçon 1: R₁= 636 620 H^-1; Tronçon 2: R₂ = 583 568 H^-1;

Tronçon 3 = Tronçon 5: R₃ = 123 340 H^-1 = R₅ ; Tronçon 4: R₄ = 663 146 H^-1.

En utilisant l'analogie avec les circuits électriques nous pouvons donner le modèle équivalent du circuit magnétique représenté fig.5. Exprimons la d.d.p magnétique V :

v pour le tronçon central V =R₃.F₃ + R₄ .F₄ + R₅.F₅ =1 094 At.

v pour le tronçon de droite V = - E ‘ - R₂.F₂ (1) avec E ‘= n'.I'= 1 600 At.

3.1 Circuit magnétique homogène

Nous reprenons le circuit de la fig.1 avec un matériau magnétique non linéaire. Ce matériau est caractérisé par sa courbe d'aimantation B(H) en négligeant le phénomène d'hystérésis. Par le théorème d'Ampère la f.m.m. totale E = n'.I'- n.I est égale à la circulation de l'excitation: E = H.l ; le flux magnétique à travers la section droite est F = B.S. Avec un changement d'échelle la caractéristique B(H) représente le flux F en fonction de la f.m.m. E. La caractéristique F( E ) ainsi obtenue est appelée caractéristique réluctive du circuit. Dans les circuits non linéaires, la notion de réluctance perd son intérêt car elle dépend de la perméabilité µ elle-même fonction de l'excitation.

3.2 Association en série de tronçons homogènes

Reprenons le circuit magnétique de la fig.3; chaque tronçon est caractérisé par sa caractéristique magnétique B_i(H_i) . Nous en déduisons la caractéristique réluctive CM_i représentant F_i(E_i ).

Les tronçons en série étant parcourus par un même flux F représenté graphiquement en OF, nous en déduisons en FM_i la f.m.m. nécessaire pour magnétiser le tronçon T_i. L'association en série impose d'ajouter les f.m.m. pour obtenir en FM la f.m.m. totale. Nous pouvons ainsi tracer point par point la caractéristique réluctive CM du circuit complet.

3.3 Association en parallèle de tronçons homogènes sans bobinages

Reprenons le circuit de la fig.4. Chaque tronçon homogène est caractérisé par sa caractéristique réluctive CM_i.

Les deux tronçons T₂ et T₃ en parallèle sont soumis à la même d.d.p magnétique représentée par OM. Le flux total est la somme des flux représentés par OF₂ et OF₃; le flux résultant est donc représenté par OF; nous pouvons ainsi tracer point par point la caractéristique réluctive CM du circuit équivalent aux deux tronçons en parallèle.

3.4 Circuit magnétisé par un seul bobinage

Lorsque le circuit magnétique comporte un seul noyau portant un bobinage de n spires parcourues par un courant d'intensité I et un ensemble de culasses, il est possible de tracer la caractéristique réluctive résultante de ce circuit par des réductions alternatives des culasses en série et en parallèle. Cette caractéristique donne alors le flux dans le noyau en fonction de la f.m.m totale E = ± n I.

3.5 Exemples de calculs de circuits magnétiques

Prenons par exemple le circuit magnétique de la fig.5 .

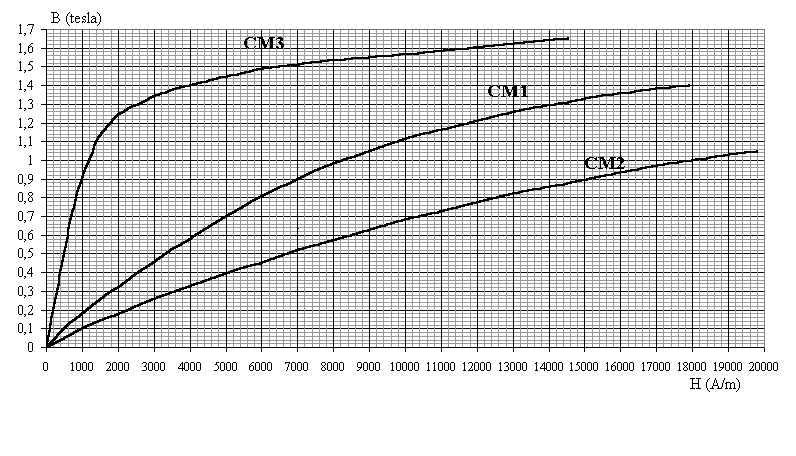
Les caractéristiques B(H) des tronçons sont donnés par la fig..8: CM1 pour T₁, CM2 pour T₂, CM3 pour T₃ et T₅; T₄ est un entrefer de perméabilité relative égale à 1.

fig.8

3.5.1 Pour I' =2A, calculons I pour avoir B₄ = 1 T dans l'entrefer

Nous avons H₄= B₄ /µ_o= 795 775 A.m^-1. B₃ = B₄ = B₅ =1T ; sur CM3 nous lisons:

H₃ = H₅ =1 100 A.m^-1 . Nous pouvons alors calculer la d.d.p magnétique V :

V = H3.l ₃ + H4.l ₄ + H5.l ₅ = 1 126 At. Le théorème d'Ampère appliqué à la ligne de champ moyenne du circuit T₂, T₃, T₄, T₅ donne : n'.I'= S H_i.l _i = H₂.l ₂ + V; nous en déduisons H₂ = 431 A.m^-1 ; sur CM2 nous lisons le champ B₂ = 0,04 T; nous calculons le flux F₂ = B₂.S₂ = 0,048 mWb. La conservation du flux donne: F = F₁+F₂ soit F₁ = 1,152 mWb. Le champ dans le tronçon T₁ vaut donc : B₁= F₁/ S₁= 1,152 T. Sur CM1 nous lisons l'excitation H₁= 10 650 A.m-1.

Le théorème d'Ampère appliqué au circuit T₁, T₃, T₄, T₅ donne: n.I= S H_i.l _i = V +H₁.l ₁ = 9 646 At;

le courant cherché a pour intensité I = 9,65 A.

3.5.2 Donnons nous I =I'= 2A et cherchons l'induction B4 dans l'entrefer

Nous ne pouvons ici résoudre directement: nous ne connaissons aucun des trois flux donc aucun champ et aucune excitation; les équations du circuit ne peuvent permettre le calcul puisque les perméabilités donc les réluctances sont inconnues. Nous avons vu ci-dessus que la connaissance de F permet de calculer I en connaissant I'; nous allons, suivant la méthode ci-dessus, tracer le graphe de I en fonction de B₄ :

Nous pouvons par interpolation entre les derniers points, calculer B₄ pour I = 2A:

B₄=0,35 + (0,4 - 0,35) (2,36 - 2) / (2,36 - 1,94) = 0,393 T.

Dans de nombreux cas nous devrons employer une méthode semblable à celle-ci: nous cherchons la grandeur qui nous permet de calculer toutes les autres de proche en proche. Nous écrivons les formules de calcul; nous abandonnons alors une des données, généralement un courant magnétisant, et nous traçons le graphe des variations de cette donnée en fonction de la grandeur choisie. Sur ce graphe nous pouvons lire pour la valeur de la donnée de l'énoncé la grandeur de départ et donc calculer toutes les autres grandeurs.

4 fuites magnétiques

Nous avons considéré dans les paragraphes précédents que le champ était parfaitement canalisé par le circuit magnétique; en réalité il n'en est pas ainsi. Le flux créé par les bobines ne passe pas entièrement dans le circuit magnétique; une partie se referme par l'air autour des spires du bobinage; il y a des fuites magnétiques

.

Une bobine de n spires parcourue par le courant I crée un flux total j_t à travers sa section droite; une partie j de ce flux est canalisée par le circuit magnétique et l'autre partie j_f se ferme autour des spires, formant le flux de fuites.

Nous pouvons caractériser la canalisation du flux par le coefficient d'Hopkinson n = j_t / j . Ce coefficient est supérieur ou égal à 1; n = 1 si le bobinage n'a pas de fuites.

Le trajet du flux de fuites est composé d'une partie dans le matériau et d'une grande partie dans l'air. La réluctance d'un tronçon étant inversement proportionnelle à la perméabilité relative µ_r, la réluctance de l'air sera très grande devant celle du matériau; nous pouvons donc considérer que le flux de fuites a un trajet dans un matériau non saturable de perméabilité µ_o constante. Le flux dans une section droite j_f est alors proportionnel à l'intensité du courant magnétisant: j_f = k. I. Le flux total de fuites à travers la bobine de n spires est: j_tf = n.j_f = k.n.I = L_f .I. La grandeur L_f est appelée inductance de fuites de la bobine.

5 énergie magnétique

Soit un circuit magnétique magnétisé par une bobine de n spires parcouru par un courant d'intensité I. Nous négligeons la résistance du bobinage et les fuites. Traçons sur la fig.10.a la caractéristique réluctive idéalisée du circuit.

Faisons croître le courant I de 0 à I₁; le flux dans la section droite croit de 0 à F₁. La croissance du flux crée dans la bobine une f.é.m induite e, comptée positivement dans le sens de I, de valeur e = -n.dj/dt. La puissance instantanée reçue par la bobine est p = -e.i ; le signe - vient de la convention générateur adoptée pour e et de la convention récepteur pour la puissance. Durant l'intervalle de temps dt, l'énergie reçue par la bobine est dw = p.dt = n.i.dj. Lorsque F croit de 0 à F₁, l'énergie totale fournie à la bobine est : ; cette intégrale est égale à l'aire hachurée sur la fig.10.a. Si nous travaillons dans la partie linéaire de la caractéristique, nous pouvons introduire l'inductance de la bobine L = n.j / i ; il vient n.dj =L.di, soit dw = L.i.di et W₁= L.I₁^² / 2.

Cette énergie est emmagasinée dans la circuit sous forme d'énergie magnétique. Elle reste stockée tant que nous maintenons le courant magnétisant; lorsque nous annulons le courant cette énergie sera restituée et pourra être transformée en une autre forme d'énergie.

Ajoutons un entrefer dans le circuit magnétique précédent; la caractéristique réluctive devient celle de la fig.3.10 .b: le flux de saturation est inchangé mais dans la partie linéaire l'entrefer augmente la réluctance. Pour magnétiser ce nouveau circuit avec une flux F₁ , il faut donc une f.m.m plus élevée: I₂ > I₁.

Lorsque nous faisons croître le courant de 0 à I₂, l'énergie fournie à la bobine est W₂, représentée par l'aire hachurée de la fig.3.10.b; nous constatons que W₂ > W₁.

La présence d'un entrefer permet d'augmenter l'énergie magnétique emmagasinée dans un circuit magnétique.

Dans toutes les applications où nous désirons stocker temporairement de l'énergie magnétique, nous utiliserons des circuits magnétiques avec entrefer; c'est par exemple le cas dans les bobines de lissage de courant.