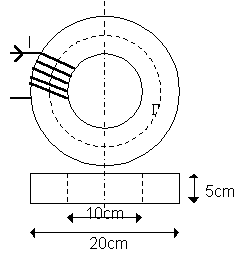
On étudie le circuit magnétique ci-dessous :
|
Le matériau est linéaire de perméabilité relative µr = 2500 |
| Calculer la longueur L de la ligne moyenne de champ G et la section droite S du tore |
Diamètre moyen D = 15 cm. L = p.D = 47 cm
Section : S = 25 cm²
Réponse |
| Calculer la réluctance du circuit magnétique |
R = L/µ.s = 60 000 1/H
µ=µo.µr = p/1000
Réponse |
| Calculer l'intensité I pour avoir B = 0,8 T |
H = B/µ = 255 A/m et H.L = N.I soit I = 80 mA
ou
F = B.S = 2 mWb ; E = N.I = R. F= 120 A.t
Réponse |
| On enlève une longueur L' = 1 cm de matériau pour former une entrefer de perméabilité relative 1. Calculer les nouvelles valeurs de la réluctance et de l'intensité pour B = 0,8 T |
On a deux tronçons en série :
T de longueur L = 46 cm perméabilité µr = 2500
T' de longueur L' = 1 cm et de perméabilité µ'r=1
Appliquer la loi d'association des réluctances
Aide |
R = L/µ.S = 58 600 1/H
R' = L'/µ'.S = 3 183 000 1/H
Rt = R + R' = 3 242 000 1/H
F = B.S = 2 mWb ; E = N.I = Rt. F= 6484 A.t
I = 4,3 A
Réponse |
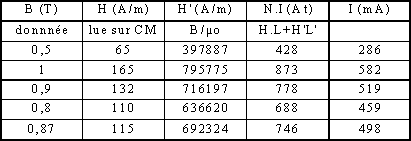
La matériau est ferromagnétique avec la caractéristique CM |
| Le circuit étant sans entrefer, calculer I pour avoir B = 0,8 T |
Lire sur CM H = 110 A/m et H.L = N.I
soit I = 34,5 mA
Réponse |
| Calculer le champ B pour un courant I = 500 mA et un circuit sans entrefer |
H = N.I / L = 1596 A/m
CM donne B = 1,42 T
Réponse |
| Calculer le champ B pour un courant I = 500 mA et un circuit avec entrefer L' = 1 mm. |
H.L + H'.L' = N.I est la seule équation disponible mais impossible de connaître à priori H/H' = µr.
Il faut donc procéder par essais successifs :
on se donne B = B' on en déduit H et H' donc I et on compare avec la valeur donnée
Aide |
|
Exercice 2 : On étudie le circuit magnétique ci-dessous :
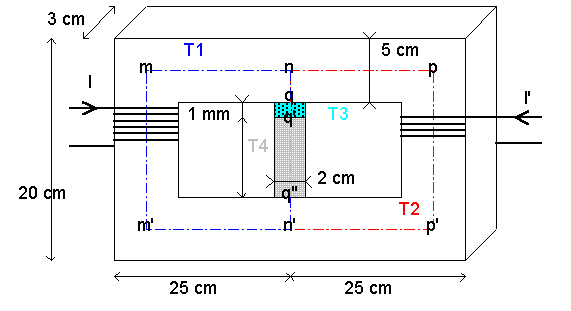
Les tronçons T1, T2 et T4 sont en matériau ferromagnétique de caractéristique CM; T3 est un entrefer.
Le circuit est magnétisé par une bobine de N = 200 spires parcourue par le courant I et une bobine de N' = 50 spires parcourue par un courant I'. |
On impose I = 5 A et on veut un champ magnétique B3 = 0,5 T dans T3 dirigé de q vers q' |
| Calculer la d.d.p.m. entre q et q" |
Pour une culasse V = H.L
avec H = B/(µo.µr)
Aide |
V = H3.L3+H4.L4 = 404 At
Pour T3 : B3 = 0,5T ; µr3 = 1 : H3=397887 A/m ; L3 = 1 mm
Pour T4 : B4 = 0,5T ; CM donne H4=60A/m ; L4 = 9,9 cm
Réponse |
| Calculer l'excitation H1 dans le tronçon T1 |
Appliquer le théorème d'Ampère au parcours q"n'm'mnqq'q"
Aide |
H1.L1+H3.L3+H4.L4 = N.I
L1 = 60 cm ; H1 = 993 A/m
Réponse |
Calculer le flux F2 circulant dans T2 de n vers p |
D'après CM B1 = 1,37 T ; F1 = B1.S1 = 2,1 mWb
Conservation du flux : F2 = F1 - F3 = 1,8 mWb
Réponse |
Calculer la valeur du courant I' |
Appliquer le théorème d'Ampère au parcours pp'n'q"q'qnp
Aide |
H2.L2-H3.L3-H4.L4 = N'.I'
L2 = 60 cm ;B2 =1,2 T ; H2 = 300 A/m
I ' = -4,48 A
Réponse |
On impose I = 4 A et I' = 1 A; on désire calculer le champ B3 dans le tronçon T3 |
| Quelle méthode doit-on employer ? |
Comme on ne connaît aucun champ, on ne connaît aucune excitation donc on ne peut exploiter les équations déduites du théorème d'Ampère
On doit donc procéder par essais successifs :
se donner B3 et calculer I' comme ci-dessus -comparer à la valeur donnée I' = 1 A
Réponse |
Calculer B3. Pour plus de précision, utiliser le zoom sur CM en cliquant ici |
1 - se donner B3=B4
2- calculer H3=B3/µo et lire H4 sur CM
3 - calculer la ddpm V = H3.L3+H4.L4
4 - Calculer H1 = (N.I - V)/L1 en déduire B1
5 - calculer F2, B2, H2
6 - Calculer I' = (H2.L2 - V)/N'
Aide |
Réponse |