Électrotechnique
x x Module 1: x
"Magnétisme" |
Chapitre 1.5
Magnétisation
des machines tournantes
|
En magnétisme, on appelle armature, l'ensemble d'un circuit magnétique et des bobinages qu'il porte.
Une machine tournante comporte deux armatures cylindriques coaxiales séparées par un entrefer:
![]() une fixe ou stator
une fixe ou stator
une tournant autour de l'axe de la machine ou rotor.
Nous étudions les armatures hétéropolaires comportant une succession de pôles magnétiques Nord et Sud. Les pôles ne pouvant exister que par paires, le nombre pair de pôles est appelé 2.p (p = Paire).
La machine possédant une symétrie cylindrique, un point M de l'entrefer sera défini par sa position angulaire mécanique qm repérée par rapport à un axe fixe généralement aligné sur l'axe d'un pôle Nord.
Nous appelons pas polaire l'écart angulaire a entre les axes de deux pôles consécutifs, donc de noms contraires; les 2.p pôles couvrant l'angle total 2.p , nous avons: a = 2.p /2.p = p / p. Tous les pôles ayant la même géométrie, le champ magnétique B créé dans l'entrefer aura la période spatiale 2.a donc la pulsation spatiale 2.p/2.a = p.
Nous supposons les machines peu ou pas saturées; dans ce cas la perméabilité magnétique µ = µo.µr du matériau magnétique est très grande devant celle µo de l'entrefer. Ceci impose:
v un champ magnétique radial dans l'entrefer, c'est à dire porté par un axe perpendiculaire à l'axe de rotation du rotor.
v une réluctance du circuit magnétique négligeable devant celle de l'entrefer; nous dirons que "la force magnétomotrice est localisée dans l'entrefer".
La succession des pôles Nord et Sud peut être obtenue de deux façons:
èpar la distribution des courants dans les conducteurs du bobinage placés dans des encoches parallèles à l'axe. L'épaisseur d de l'entrefer est alors faiblement modulée par la profondeur des encoches: nous dirons que l'armature est à pôles lisses.
èpar des pièces polaires saillant radialement de l'armature et portant des bobines coaxiales de la pièce polaire. L'épaisseur de l'entrefer est alors variable suivant la position par rapport aux pièces polaires: nous dirons que l'armature est à pôles saillants.
Le champ créé par une armature dépend :
du nombre de pôles et de phases
de la nature du courant magnétisant : continu ou alternatif
de la nature des pôles : lisses ou saillants
du mouvement de l'armature : fixe ou tournante
Nous allons étudier les principales armatures rencontrées dans les machines tournantes.
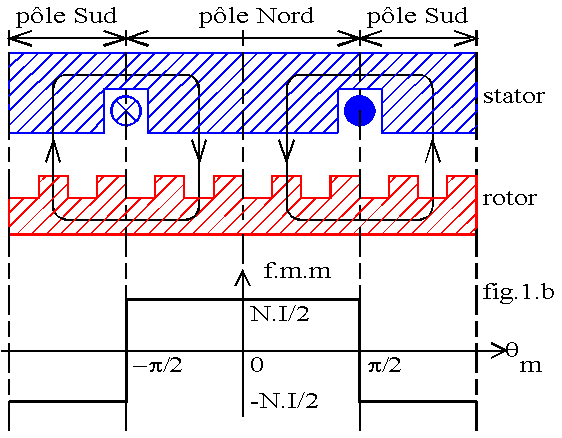
2.1 Stator à pôles lisses, bipolaire et à bobine diamétrale
Le stator de la machine comporte une bobine de N spires contenue dans deux encoches diamétralement opposées (fig.1.a). Cette bobine, alimentée par un courant continu d'intensité I, crée une excitation H canalisée par le circuit magnétique. L'allure des lignes de champ est donnée sur la figure 1a.
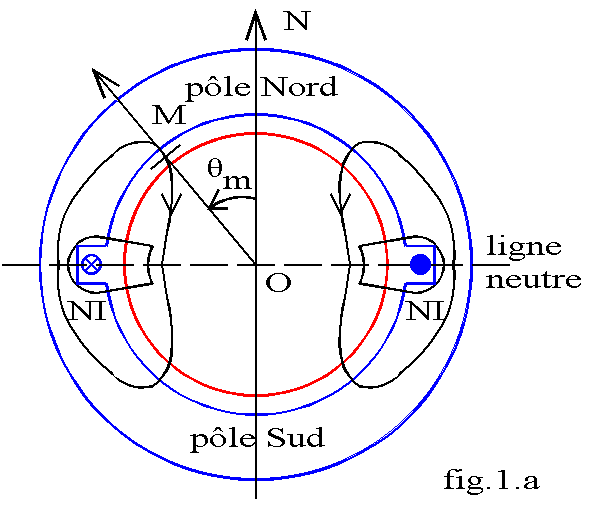
En négligeant la réluctance du fer devant celle de l'entrefer d'épaisseur d et en appliquant le théorème d'Ampère le long d'une ligne de champ il vient: ![]() .
.
La force magnétomotrice (en abrégé f.m.m.) est E(M) = H.d = N.I/2.
La force magnétomotrice est quasi constante sous un pôle et change de signe lorsqu'on franchit la ligne neutre séparant les pôles. Le graphe E (qm) est donc un créneau de période 2.p (fig.1b).
2.2 Stator à pôles lisses, bipolaire à enroulement réparti
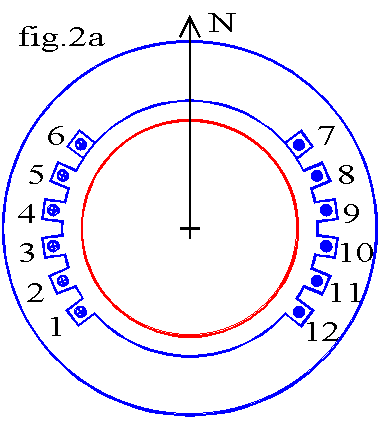
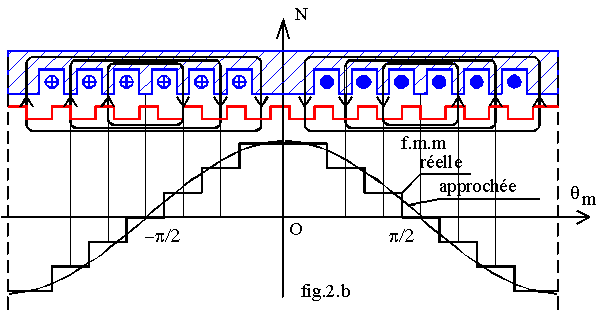
Pour des raisons technologiques, les N conducteurs de la bobine ne sont pas situés dans la même encoche mais répartis dans plusieurs encoches (fig.2a). La fig.2.a donne une représentation développée de la machine. Les points de l'entrefer placés au voisinage de qm = p/2 ne voient aucune ligne de champ, donc E = 0; lorsque qm diminue, les lignes de champ bouclent d'abord les deux conducteurs 3 et 4 : soit E = I;. ensuite les lignes bouclent les quatre conducteurs 2, 3, 4, 5 : E = 2.I ; Enfin pour q voisin de 0, les six conducteurs sont bouclés: E = 3.I. Le champ est représenté par une fonction constante par intervalles.
En disposant judicieusement les encoches, nous pouvons obtenir une fonction très voisine d'une sinusoïde.
Si nous adoptons la forme approchée dite f.m.m à répartition sinusoïdale, nous avons :
E (qm) = 2.K.N.I.cos(qm), K étant le facteur de bobinage dépendant de la répartition des encoches sur le stator.
On peut définir la f.m.m. dans un espace électrique de représentation vectorielle (fig.2.b):
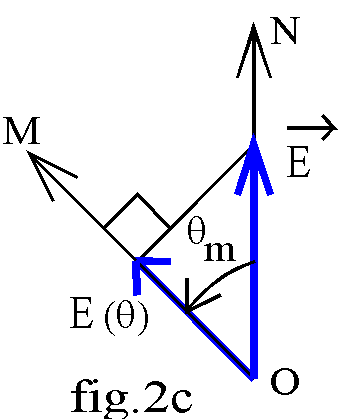
ON représente l'axe du bobinage ou l'axe d'un pôle Nord, le vecteur f.m.m.
![]() . Si nous projetons ce vecteur sur l'axe OM représentant la position du point M dans l'entrefer, nous obtenons la f.m.m. E(qm) = ||
. Si nous projetons ce vecteur sur l'axe OM représentant la position du point M dans l'entrefer, nous obtenons la f.m.m. E(qm) = || ![]() ||.cos(qm).
||.cos(qm).
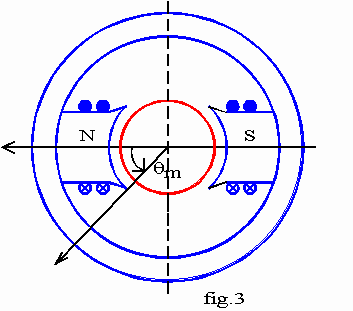
2.3 Stator à pôles saillants, bipolaire
La fig.3 donne un exemple de machine bipolaire à pôles saillants. La f.m.m. est quasi constante sous un pôle saillant et nulle en dehors des pôles.
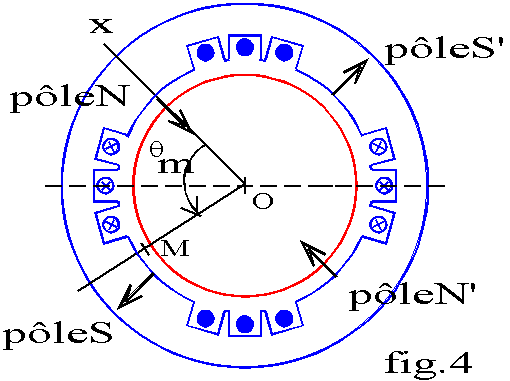
2.4 Stator multipolaire à pôles lisses
Si le stator possède 2p pôles (fig.4), nous obtenons le même type de répartition de la f.m.m. que pour la machine bipolaire. Le champ magnétique change de sens, chaque fois que l'on change de pôle, c'est à dire lorsqu'on parcourt un pas polaire. La période de la f.m.m devient donc 2.a = 2.p/ p et la pulsation p
Pour une répartition sinusoïdale, nous avons, E(qm) = || ![]() ||.cos(p.qm), le vecteur f.m.m. gardant la même valeur.
||.cos(p.qm), le vecteur f.m.m. gardant la même valeur.
En appelant qe = p.qm l'angle électrique, la forme de la f.m.m. est la même quel que soit le nombre de pôles.
Pour la suite, nous étudierons les machines en angles électriques, ce qui évite d'envisager diverses valeurs du nombre 2.p de pôles.
2.5 Expression de la force magnétomotrice
Toutes les armatures ci-dessus donnent une f.m.m constante dans le temps et variable dans l'espace. La répartition spatiale de la f.m.m E(qm) a une période égale à deux pas polaires; pour avoir une étude indépendante du nombre de pôles, nous utilisons l'angle électrique.
La fonction E(qe) a la période 2.p quel que soit le nombre de pôles. Cette fonction étant périodique, nous pouvons la décomposer en série de Fourier; l'origine étant prise sur l'axe d'un pôle Nord, la fonction est paire et alternative, son développement ne contient que des termes en cosinus de rang impair:
E(qe) = E1.cos(qe)+ E3.cos(3.qe)+E5.cos(5.qe)+ ... +E2k+1.cos[(2k+1).qe ]+...
Un stator à 2p pôles , alimenté en courant continu, crée dans l'entrefer une f.m.m constante dans le temps et variable dans l'espace; la fonction E(qm) a pour période deux pas polaires 2.a = 2.p / p
3.1 Rotor à répartition sinusoïdale de f.m.m
Nous raisonnons en angles électriques donc sur une machine bipolaire. Le rotor représenté sur la fig.5.a, porte un bobinage semblable à celui du stator de même type (cf ¶ 2.2); nous ne représentons qu'une encoche par pôle pour alléger le dessin. Le rotor tourne à la vitesse mécanique angulaire W dans le sens direct.
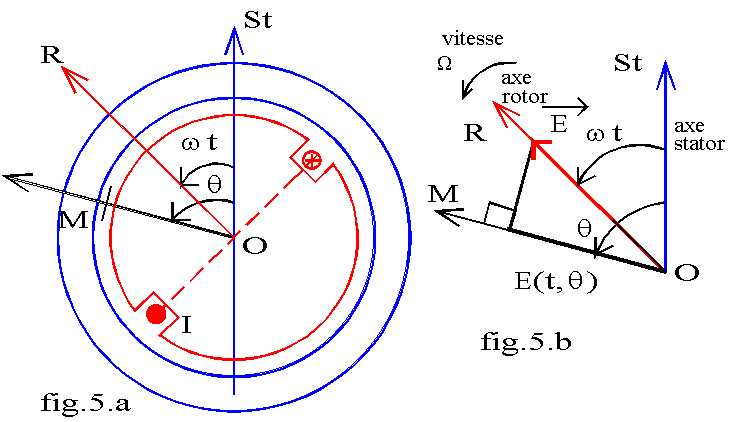
Pour un observateur tournant avec le rotor, la f.m.m. apparaît constante dans le temps et variable dans l'espace : elle est maximale sur l'axe OR du pôle N du rotor, nulle sur la ligne neutre. Nous supposons que le bobinage crée une répartition spatiale sinusoïdale. La f.m.m. peut donc être représenté par le vecteur ![]() porté par l'axe OR ( fig.5.b). Soit OSt un axe fixe lié au stator, l'angle mécanique (OSt,OR) est W.t, l'angle électrique correspondant est W.t/p = w.t en appelant w la pulsation électrique. En un point M de l'entrefer repéré par l'angle électrique qe = ( Ost,OM), la f.m.m est représentée par la projection de
porté par l'axe OR ( fig.5.b). Soit OSt un axe fixe lié au stator, l'angle mécanique (OSt,OR) est W.t, l'angle électrique correspondant est W.t/p = w.t en appelant w la pulsation électrique. En un point M de l'entrefer repéré par l'angle électrique qe = ( Ost,OM), la f.m.m est représentée par la projection de ![]() sur OR; nous avons
sur OR; nous avons
E (qe , t) = || ![]() ||.cos(OR,OM) = ||
||.cos(OR,OM) = || ![]() ||.cos(.qe - w.t).
||.cos(.qe - w.t).
Cette f.m.m. a une double périodicité :
![]() dans le temps : la pulsation est w et la période 2p / w
dans le temps : la pulsation est w et la période 2p / w
 dans l'espace: la période est 2p en angles électriques donc 2p / p en angles mécaniques
dans l'espace: la période est 2p en angles électriques donc 2p / p en angles mécaniques
Si le rotor tourne à vitesse - W , l'expression de la f.m.m est : E (qe , t) = || ![]() ||.cos(.qe + w.t).
||.cos(.qe + w.t).
3.2 Répartition quelconque de f.m.m.
Un rotor à 2.p pôles, alimenté en continu et tournant à la vitesse angulaire W crée dans l'entrefer une f.m.m. tournante variable en fonction du temps et de l'espace E(t ,q) de pulsation spatiale p et temporelle w = p.W; sa décomposition en série de Fourier est de la forme : E(t ,qm) = S E2k+1.cos[(2k+1).p(qm - W.t) ]. Chaque harmonique de rang n impair peut être considéré comme créé par un rotor à 2.n.p pôles et tournant à vitesse angulaire W.
Un rotor à 2.p pôles , alimenté en courant continu, tournant à la vitesse mécanique W, crée dans l‘entrefer une f.m.m. variable dans le temps et dans l'espace; la fonction E (t ,qm) a pour pulsation temporelle la vitesse électrique w = p. W et pour pulsation spatiale le nombre de paires de pôles
4.1 Force magnétomotrice
Nous reprenons l'armature fixe à 2.p pôles décrite au ¶2 ; cette armature alimentée par un courant d'intensité continue I, crée une f.m.m. fixe dans le temps et variable dans l'espace; en supposant la machine peu ou pas saturée, la réluctance du fer est négligeable devant celle de l'entrefer et l'amplitude de l'induction est proportionnelle au courant créateur: E(q) = c.I.f(q).
Nous alimentons maintenant le bobinage par un courant sinusoïdal d'intensité instantanée
i(t) = Im.cos(w.t). La f.m.m dépend maintenant de l'angle q mais aussi du temps puisque le courant magnétisant varie. Nous avons E(t ,q) = c.i(t).f(q) = c.Im.f(q).cos w.t.
La répartition spatiale c.f(q) de période 2.p / p en angle mécanique peut être décomposée en série de Fourier sous la forme c.f(q) = S C2k+1.cos[(2k+1).p.qm] ; nous pouvons donc écrire:
E(t ,q) = S [ Im.C2k+1.cos [(2k+1).p.qm].cos w.t ].
4.2 Répartition sinusoïdale : théorème de Leblanc
Etudions le cas d'une répartition sinusoïdale de la f.m.m ; dans l'expression ci-dessus, nous ne conservons que le terme fondamental : E(t ,q)= Im. C1.cos (p.qm ).cos w.t.
Utilisons la représentation graphique dans l'espace électrique (fig.6). La f.m.m peut être représentée par un vecteur porté par l'axe du stator OSt.
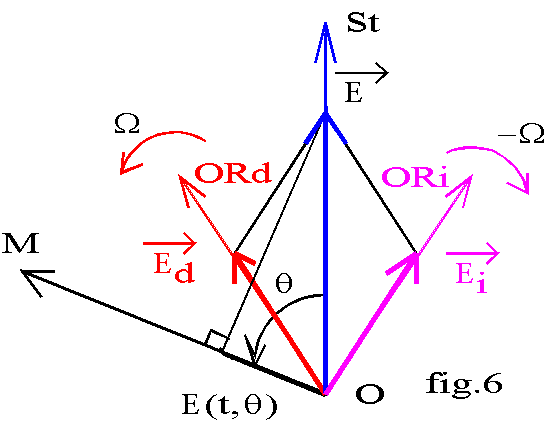
Ce vecteur est de module ||![]() || = Im.C1.cos w.t. La f.m.m au point M de l'entrefer est représentée par la projection de ce vecteur sur OM. Nous avons :
|| = Im.C1.cos w.t. La f.m.m au point M de l'entrefer est représentée par la projection de ce vecteur sur OM. Nous avons :
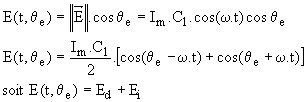
Le premier terme Ed est la f.m.m. d'un rotor alimenté par le courant Im / 2 et tournant à la vitesse mécanique W = w/p. Le deuxième terme Ei est la f.m.m d'un rotor alimenté par le courant Im / 2 et tournant à la vitesse mécanique -W = - w/ p.
A t = 0, nous avons i(0) = Im , et à cet instant les vecteurs tournants ![]() d et
d et ![]() i sont portés par l'axe OSt.
i sont portés par l'axe OSt.
Théorème de Leblanc : un stator alimenté par un courant sinusoïdal de pulsation w est équivalent à deux rotors à répartition sinusoïdale de f.m.m. Les deux rotors tournent à vitesse mécanique |W| = w / p , l'un dans le sens direct, l'autre dans le sens inverse. Les axes ORd et ORi de ces rotors passent sur l'axe OSt de la phase statorique lorsque le courant y est maximal.
4.3 Répartition quelconque de f.m.m
Si la répartition spatiale n'est pas sinusoïdale, nous pouvons décomposer la f.m.m. en série de Fourier sous la forme :
E(t ,q) = S C2k+1.cos[(2k+1).p.qm].Im. cos(p.W.t). L'harmonique 2k+1 s'écrit :
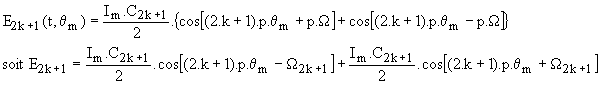
en posant W2k+1= W / (2.k+1).
Cette f.m.m. peut être considérée comme résultant de la superposition des f.m.m. de deux rotors à répartition sinusoïdale à (2k+1).2.p pôles tournant en sens inverse à la vitesse W2k+1= w /(2.k+1)p.
Une armature triphasée est formée de trois bobinages à 2.p pôles, identiques, dont les axes ON1, ON2 et ON3 sont décalés mécaniquement de 2.p/3.p donc électriquement de 2.p/3.
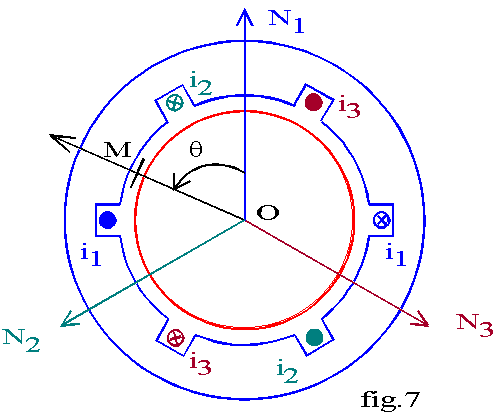
Ces bobinages sont parcourus par un système de courants sinusoïdaux triphasé équilibré direct d'amplitude Im et de pulsation w .
Un point M de l'entrefer est défini par son angle polaire électrique q = (ON1,OM) = q1. Par rapport aux autres phases, nous avons : q2 = (ON2,OM) = q - 2.p/3 et q3 = (ON3,OM) = q - 4.p/3 .
Suivant les résultats du paragraphe 4, nous pouvons écrire les f.m.m créées par les trois phases en M:
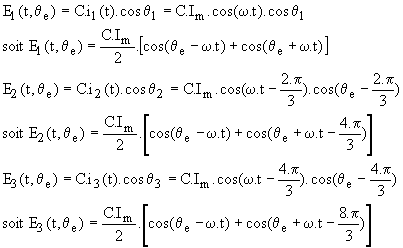
La f.m.m résultante est la somme de celles créées par les trois phases. Nous avons :
cos(a - 4.p/3) = cos(a + 2.p/3) et cos(a - 8.p/3) = cos(a - 2.p/3); la somme de trois grandeurs triphasées équilibrées cos(a)+ cos(a - 2.p/3)+ cos(a +2.p/ 3) est nulle. Nous en déduisons :
![]()
Chaque phase est équivalente à deux rotors tournant en sens inverses. Les trois rotors tournant dans le sens direct sont en phase et passent sur l'axe de chaque phase à l'instant où le courant y est maximal. Les trois rotors tournant dans le sens inverse sont triphasés dans l'espace et créent une f.m.m résultante nulle.
Théorème de Ferraris : un stator triphasé à deux p pôles et à répartition sinusoïdale de f.m.m, parcouru par un système de courants sinusoïdaux triphasés équilibrés de pulsation w, crée une f.m.m. unique tournant à la vitesse mécanique W = w / p. L'axe du rotor équivalent au stator rencontre l'axe des phases dans l'ordre de succession des courants (sens direct = système direct, sens inverse = système inverse) et passe sur l'axe de chaque phase lorsque le courant y est maximal.
La fig.8 montre l'évolution du champ avec le temps :
![]() à t = 0, le courant est maximal dans la phase 1 donc l'axe du pôle Nord est sur l'axe ON1 de la phase 1.
à t = 0, le courant est maximal dans la phase 1 donc l'axe du pôle Nord est sur l'axe ON1 de la phase 1.
 à t = T/3, le courant est maximal dans la phase 2 donc l'axe du pôle Nord est sur l'axe ON2 de
à t = T/3, le courant est maximal dans la phase 2 donc l'axe du pôle Nord est sur l'axe ON2 de
la phase 2.
 à t = 2.T/3, le courant est maximal dans la phase 3 donc l'axe du pôle Nord est sur l'axe ON1 de la phase 3.
à t = 2.T/3, le courant est maximal dans la phase 3 donc l'axe du pôle Nord est sur l'axe ON1 de la phase 3.
En un point M de l'entrefer repéré par l'angle q1 = (ON1,OM), le champ magnétique a une direction OM fixe et un module variable. Ce type de champ est dit tournant. En fait la répartition de B glisse plutôt le long de la surface du stator puisque la direction du champ est toujours radiale.
