è L'alimentation se fait par une source de tension idéale et un diviseur capacitif.

è La charge est formée de trois branches de type courant sinusoïdal triphasé

è La conversion est assurée par trois bras d'onduleur en parallèle

è La commande de chaque bras est de type adjacente, c'est à dire que chaque interrupteur est fermé sur une demie période, et les commandes des bras sont décalées d'un tiers de période

è Lorsque K1 est fermé, van = E/2 et lorsque K'1 est fermé,

van = -E /2

è Les tensions composées se calculent par différence :

uab = van - vbn

è Le courant source est is = ik1 + ik2 + ik3 ; il est de période T/6. Si le déphasage j = (ia, van) < p /3, is > 0 et si j > p/3, le courant is est d'abord négatif puis positif; pour des courants charge équilibrés, sa valeur moyenne est 3.Imax.cosj /p

Les graphes de vk1 et ik1 montrent que K1 doit être commandé à l'ouverture et à la fermeture

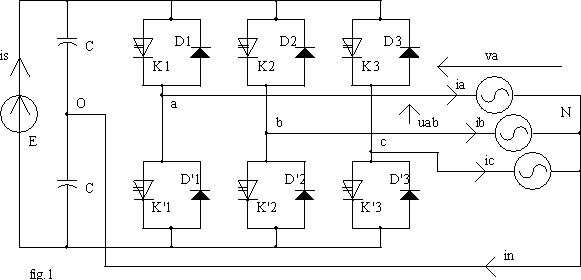
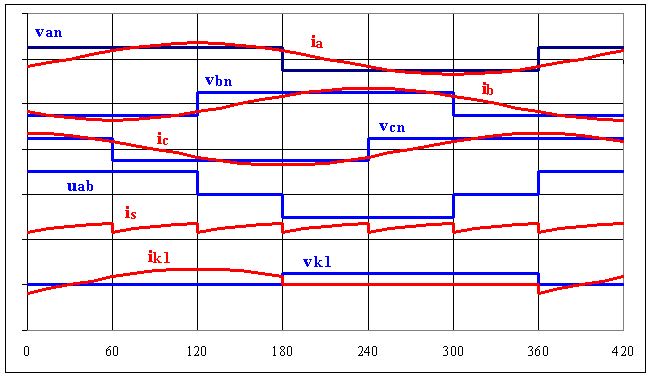
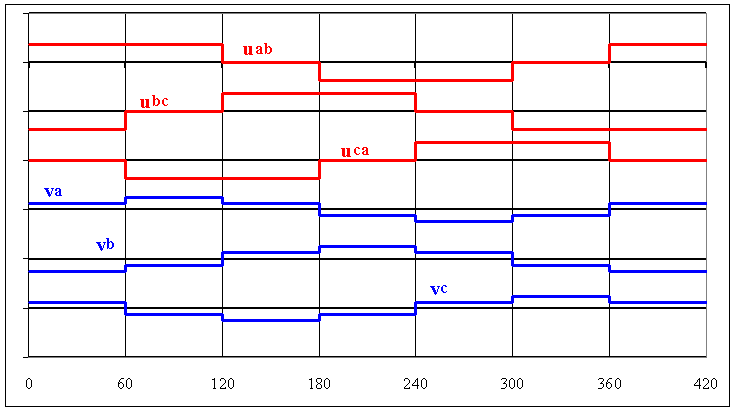
On utilise la méthode harmonique

è La tension simple est alternative donc n'a que des harmoniques impairs.

è L'harmonique de rang n = 2.k+1 de la tension va est :

van = [2.E /(p.n)].sin(n.q) ; celui de la tension vb est déphasé de

a = - 2.p.n/3 et celui de vc est déphasé de b = 2.p.n/3

Si n = 1, 7,13, 19, .... , 6.p+1 : a = - 2.p.n/3 et b = 2.p.n/3; van, vbn, vcn forment un système triphasé d'ordre direct

Si n = 3, 9,15, 18, .... , 6.p : a = 2.pet b = 2.p; van = vbn = vcn forment un système homopolaire

Si n = 5, 11,17, 23 , .... , 6.p - 1 : a = + 2.p.n/3 et b = - 2.p.n/3; van, vbn, vcn forment un système triphasé d'ordre inverse

è Les tensions composées n'ont pas d'harmoniques de rang multiple de 3 ; pour les autres harmoniques, on a Uabn = Ö3.Van

è A la fréquence n.f l'impédance de la charge R - L est

Zn = R + j.n.L.w = (Zn ; jn)

è L'harmonique de rang n du courant ia est :

ian = [2.E /(p.n.Zn)].sin(n.q - jn)

è Si la charge est équilibrée, le courant dans le fil neutre ne comporte que des harmoniques de rang multiple de 3 :

in = 3.(ia3 + ia6 + ia9 + ...)

Pour une charge équilibrée, on ne connecte généralement pas le fil neutre; on peut lors supprimer le diviseur capacitif .

è L'onduleur impose alors les tensions composées : par exemple lorsque K1 et K'2 conduisent uab = E, lorsque K1 et K2 conduisent uab = 0 ...

è Les tensions composées et la charge étant équilibrées, les courants sont équilibrés et donc les tensions simples aussi; on en déduit va + vb + vc = 0 ; avec uab = va - vb, ubc = vb - vc, on en déduit va = (2.uab + ubc) /3 , vb = (2.ubc + uca) /3 , vc = (2.uca + uab) /3

è Les tensions simples n'ont pas d'harmoniques de rang multiple de 3; pour les harmoniques 1, 5, 7, 11 ... van = [2.E /(p.n)].sin(n.q)