Exercice 1 :
On étudie le montage ci-dessous :
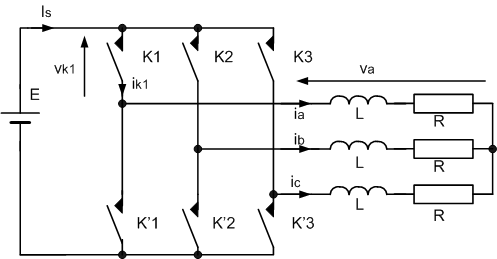
on donne :
è la tension d'alimentation E = 300 V
è les composants de la charge : R = 12 W et L = 10 mH
Le fondamental de la tension va est de fréquence f = 500 Hz |
On utilise une commande adjacente. K1 est fermé de 0 à T/2 |
1.1 |
Donner les intervalles de fermeture des six interrupteurs sur une période |
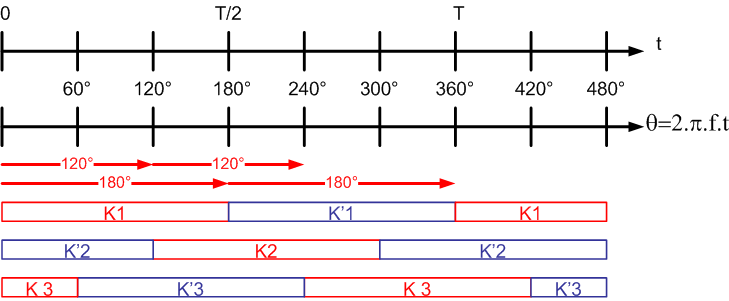 . .
Cliquez ici |
1.2 |
Tracer les tensions uab et va. |
|
1.3 |
Calculer les harmoniques de la tension va |
Pour les rangs k = 1, 5, 7, 11, ... les harmoniques de la tension va sont égaux à ceux de la tension van avec fil neutre et diviseur capacitif, c'est àdire ceux d'une fonction en créneau alternatif d'amplitude E/2
Les harmoniques de rang multiple de 3 sont nuls.
Pour k impair et différent de 3.k', Vakmax = 2.E/p.k
Va1 max = 191 V , Va5 max = 38,2 V , Va7 max = 27,3 V ,
Va11max = 17,4 V ....
Cliquez ici |
1.4 |
Calculer les harmoniques du courant ia |
Connaissant l'harmonique de rang k de la tension, on calcule l'impédance d'une phase Zk = R + j.k.2.p.f.L et on en déduit Iak = Vak /Zk
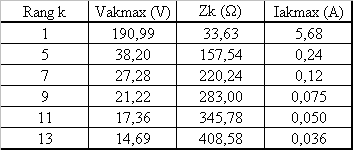
Cliquez ici |
1.5 |
Montrer que l'on peut négliger les harmoniques du courant, en déduira l'expression de ia(t). |
Les harmoniques de ia sont au minimum d'amplitude 23 fois plus petite que le fondamental; on peut donc les négliger et écrire ia(t) = 5,68.cos(2.p.f.t - j) avec
j = arg Z à la fréquence f soit j =1,21 rd = 69,1 °
Cliquez ici |
1.6 |
Calculer les puissances active et réactive fournies à la charge triphasée |
Le courant étant sinusoïdal, seul le fondamental de va est à prendre en compte : va1 = 191.sin((2.p.f.t )
P = 3.Va1eff.Iaeff.cos j = 3. 135 x 4 x 0,36 = 580 W
Q = 3.Va1eff.Iaeff.sin j = 1 520VAR
Cliquez ici |
1.7 |
Calculer la puissance apparente fournie à la charge et le facteur de puissance |
Vaeff = E.Ö(2) / 3 =141,4 V ; S = 3.Vaeff.Iaeff =1 704 VA
Fp = P / S = 0,34
Cliquez ici |
1.8 |
Calculer la valeur moyenne du courant fourni par la source E |
Si on néglige toutes les pertes P = E.Ismoy donc
Ismoy = 1,94 A
Cliquez ici |
1.9 |
Représenter la tension et le courant d'un interrupteur |
|
1.10 |
En déduire comment choisir l'interrupteur |
Cliquez ici |
On utilise une commande MLi calculée. La commande de K1 est construire à partir de trois signaux s du type ci-dessous :
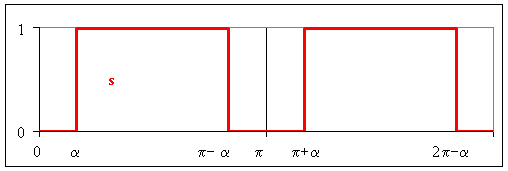
Vcom = s1 - s2 + s3 avec pour s1, a1 = 30°, pour s2 , a2 = 40° et pour s3, a3 = 50°. Lorsque vcom = 1, K1 est fermé et pour s =0, K1 est ouvert; la commande de K'1 est complémentaire de celle de K1 et les deux autres bras sont commandés de façon identique avec un déphasage de 120°
|
1.11 |
Représenter les signaux s1, s2, s3, Vcom et la tension fictive van que l'on aurait aux bornes d'une phase dans le montage avec diviseur capacitif et fil neutre. |
|
1.12 |
Calculer les harmoniques de la tension van et en déduire ceux de la tension va |
Le calcul a été effectué au chapitre 7.1 :
chaque fonction si a des harmoniques impairs d'amplitude Ai = (4/p.k).cos(k.ai)
La fonction s a pour harmonique de rang k : Ak1 - Ak2 + Ak3
La fonction Van a pour harmonique Vankmax = (E/2).(Ak1 - Ak2 + Ak3)
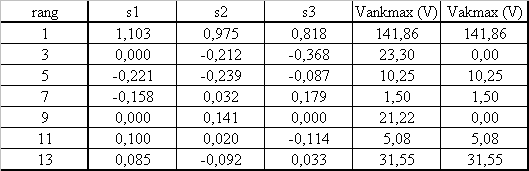
La tension va n'a pas d'harmonique de rang multiple de 3, les autres sont identiques à ceux de Van.
Cliquez ici |
1.13 |
Pour calculer les harmoniques du courant, compléter le tableau ci-dessous
|
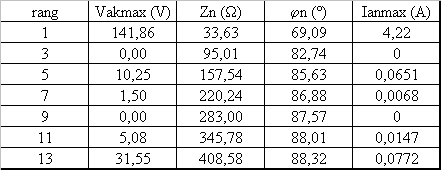
Ce courant est quasi sinusoïdal : ia = 4,22. sin(2.p.f.t - 1,21)
Cliquez ici |
1.14 |
Calculer les harmoniques du courant ia . Que peut-on dire de ce courant ? |
Le courant étant sinusoïdal, seul le fondamental de va est à prendre en compte : va1 = 142.sin((2.p.f.t )
P = 3.Va1eff.Iaeff.cos j = 3. 100 x 2,98 x 0,36 = 320 W
Q = 3.Va1eff.Iaeff.sin j = 839 VAR
Cliquez ici |
1.15 |
Calculer les puissances active et réactive fournies à la charge |
La valeur efficace de Va peut être déduite de celle de ses harmoniques :
Vaeff = Ö(SVakmax²/2) = 103 V ; S = 3.Vaeff.Iaeff = 922 VA
Fp = P / S = 0,35
Cliquez ici |
1.16 |
Calculer le facteur de puissance de la charge |
|
Exercice 2 : On étudie le montage ci-dessous :

Les tensions va, vb, vc forment un système sinusoïdal triphasé équilibré d'ordre direct, de valeur efficace V = 400 V et de fréquence f = 50 Hz; on donne va = V.Ö2.sin(2.p.f.t).
K1 est commandé à la fréquence f, il est fermé de 0 à T/3.
On suppose le courant is parfaitement lissé par l'inductance Ls.
|
3.1 |
Représenter les tensions simples de la charge, la tension us aux bornes d'un bras, le courant ia et son fondamental iaf.
|
iaf est maximum pour q = 60 ° et va pour q = 90 °, on a donc j = 60 - 90 = -30 °
Cliquez ici |
3.2 |
En déduire, le déphasage j = (iaf, va) |
us est de période T/6 soit 30 ° en angle. De 0 à 60 ° K1 et K'2 conduisent donc us = va - vb = uab = Umax.sin(q + p/6)
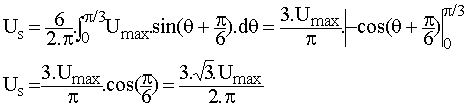
Umax = Ö3.Vmax = Ö6.V = 980 V et Us =810 V
Comme la tension moyenne aux bornes de Ls est nulle, E = Us = 810 V
Cliquez ici |
3.3 |
Calculer la valeur moyenne de la tension us; en déduire la valeur de E |
|
| 3.4 |
On veut fournir une puissance active P = 50 kW à la charge. Calculer la valeur efficace de iaf, celle de ia et la valeur moyenne de is |
Cliquez ici |
3.5 |
Représenter les graphes des grandeurs vk1 et ik1. |
A l'amorçage de K1, on a vk1 > 0 et ik1 > 0
Au blocage de K1, on a vk1 < 0
ik1 est toujours positif durant la fermeture ; on peut utiliser un thyristor
Cliquez ici |
3.6 |
Comment doit-on choisir l'interrupteur K1 ? |
L'inductance L interdit la discontinuité des courants ; avant l'ouverture de K1, ik1 = ia = Is et ik2 = 0 ; donc juste après la commande de K2 en T/3, K1 continue à conduire jusqu'à ce que ce que ik2 = ib = Is
On retrouve un phénomène identique à l'empiètement dans un redresseur P3
Cliquez ici |
En réalité, chaque phase de la charge n'est pas un générateur idéal mais possède une inductance série L = 1 mH en série avec le générateur de tension |
3.7 |
Montrer qu'à la fermeture de K2, K1 et K2 conduisent simultanément.
|
Le schéma durant la commutation est donné ci-dessous 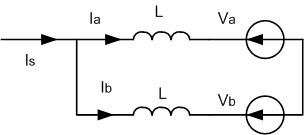
ia + ib = Is ; va + L.dia/dt = vb + Ldib/dt ; dia + dib = dIs = 0 donc
2.L.dia/dt = vb - va = - uab ; en posant q = 2.p.f.t = w.t et X = L.w,
2.X.dia/dq = -Umax.sin(q + p/6) ; ia = A + (Umax/2.X).cos(q + p/6)
ia(q = 2.p/3) = Is donc A = Is - (Umax/2.X).cos(5.p/6)
ia = 1 412 + 1 559.cos(q + p/6) ; la commutation se termine pour q1 avec
ia =0 donc cos(q1 + p/6) = -1412 /1559 , q1 = 125 °; la ommutation dure donc 5 °; comme 360° coorrespond à une période de 20 ms , la durée est de 0,28 ms.
Cliquez ici |
3.8 |
Calculer l'intensité ia durant la commutation si Is garde la valeur calculée ci-dessus.
Combien de temps dure la commutation ? |
De 0 à p/3 , us = uab = Umax.sin(q + p/6) = E -Ls.dis/dt
Xs.dis/dq = E - Umax.sin(q + p/6) ; Xs.dis = A + E.q + Umax.cos(q + p/6)
is est extrémal pour dis = 0 soit pour uab = E ; ce qui donne q1 = 25,8°
Pour q < q1, E > uab donc is augmente et pour q > q1, E < uab donc is diminue ; on aura donc :
Xs.Ismin = Xs.is(0) = A + Umax.cos(p/6) = A + 849 V
Xs.Ismax = Xs.is(q1) = A + E.q1 + Umax.cos(q1 + p/6) = A + 915 V
Xs.DIs = 66 V donc Xs = 66 W et Ls = 210 mH
Cliquez ici |
On abandonne l'hypothèse d'un courant is parfaitement lissé avec une charge d'impédance nulle |
3.9 |
Calculer l'inductance Ls pour que l'ondulation crête à crête de is soit égale à 1 A
|
La valeur efficace du fondamental de u est 127,3 / Ö2 = 90 V; il faut donc une impédance de module Z = Ö(R² + X'²) = 90 mW soit X = - 80,6 mW ou X = 80,6 mW
X' = L.w - 1/C.w donne L.C.w² -X'.C.w - 1 = 0 avec les deux valeurs de X' on a deux solutions positives ( une dans chaque cas) : 35 644 rd/s soit 5 676 Hz et 41 017 rd/s soit
6 528 Hz. Si on veut garder un courant en avance sur la tension, on choisira 5 676 Hz
Cliquez ici |