L'onduleur monophasé de tension réalise la conversion d'une source de type branche tension continue vers une branche de type courant alternatif. La commande de l'onduleur impose la tension aux bornes de la charge.
1.1 Étude structurelle
Le montage est représenté ci-contre : 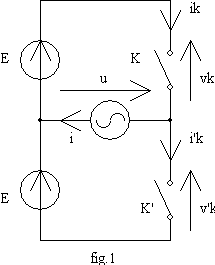
L'alimentation se fait par deux sources idéales de tension continues; la charge est un branche de type courant, imposant une intensité i sinusoïdale.
Les règles de structure imposent que :
v K et K' ne peuvent être fermés simultanément
v K et K' ne peuvent être ouverts simultanément
Ils doivent donc avoir des états complémentaires.
Comme la tension u doit être alternative, les temps de fermeture de K et de K' doivent être égaux. Le plus souvent, on fonctionne en onde rectangulaire, le fonctionnement en onde MLI étant également possible.
Dans le premier mode de commande, K est fermé de 0 à T/2; on a alors vk = 0, u = E, v'k = 2.E, ik = i et
i'k = 0. De T/2 à T, K' est fermé; on a alors v'k = 0, u = -E, vk = 2.E, ik = 0 et i'k = i.
La fig.2 donne l'allure des grandeurs pour une branche courant inductive.
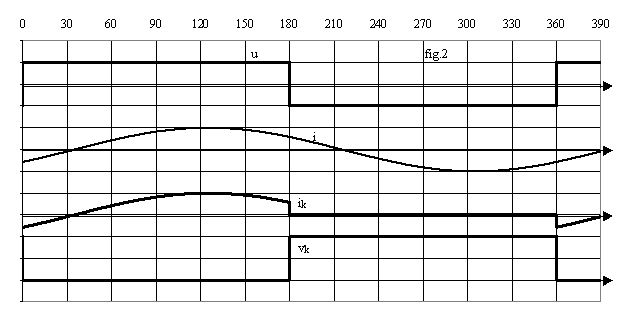
1.2 Choix des interrupteurs
Les interrupteurs K et K' doivent être unidirectionnels en tension et bidirectionnels en courant.
Il sont formés d'un interrupteur commandé et d'une diode tête-bêche. La diode conduit durant les intervalles de temps où i est négatif.
L'allure de ik et de vk montre que l'interrupteur doit être commandé à l'ouverture et à la fermeture. Cependant, suivant la nature de la charge, on peut simplifier la commande :
Ø si la charge est inductive, à t = 0, i < 0; la diode conduit de 0 à t1 et l'interrupteur commandé de t1 à T/2. On peut alors utiliser un interrupteur de type thyristor dual, commandé à l'ouverture et qui se ferme naturellement dès que le courant devient positif.
Ø si la charge st capacitive, , à t = 0, i > 0; l'interrupteur commandé conduit de 0 à t1 et la diode de t1 à T/2. Le blocage de l'interrupteur commandé se fait alors naturellement par annulation du courant et on doit seulement commander la fermeture. On peut alors utiliser un thyristor.
Si on utilise un transistor bipolaire, on doit utiliser la structure ci-contre : 
En effet lorsque le transistor est commandé à la fermeture, il ne contrôle plus le courant et peut être traversé par un courant inverse; le fonctionnement inversé du transistor avec un faible gain peut être dangereux.
On peut éviter la conduction inverse en plaçant une diode Ds en série avec le transistor. Cette diode a l'inconvénient d'augmenter la chute de tension dans l'interrupteur donc les pertes de conduction.
On peut aussi polariser négativement la base de Tr tant que le courant i est négatif pour forcer son blocage mais cela complique la commande car on doit détecter les passage à zéro de i pour débloquer Tr.
Si on utilise un transistor MOS, cet interrupteur possède une diode de structure intégrée; cette diode peut être utilisée pour conduire le courant négatif mais cette diode est de mauvaise qualité en commutation. En basse fréquence, la diode de structure peut être utilisée à condition de ralentir la commutation du MOS; en haute fréquence, cette diode doit être neutralisée en plaçant une diode en série avec le MOS et une diode rapide tête-bêche suivant un montage identique à celui de la fig.3.
Pour les fortes puissances et une fréquence maximale de l'ordre de 1 kHz, on peut utiliser un thyristor GTO.
Dans tous les cas, afin d'éviter une conduction simultanée de K et K' on doit réaliser l'emboîtement des commandes. Lorsqu'on commande la blocage de K, on ne doit pas débloquer simultanément K'; on doit attendre le blocage effectif de K et commander K' au bout d'un temps supérieur au temps de blocage toff.
1.3 Courant source
Le courant dans le générateur supérieur est égal à i de 0 à T/2 et à 0 de T/2 à T.
Le courant charge est de la forme i = Imax.sin(wt-j). Le courant moyen fourni par le générateur supérieur est donc :
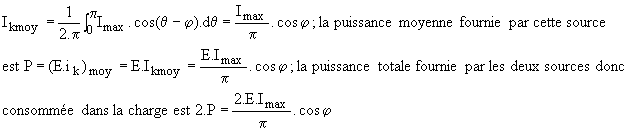
1.4 Étude du courant sur charge R - L.
Étudions la forme réelle du courant lorsque la charge est formée d'une résistance R en série avec une inductance L.
Ø calcul direct : de 0 à T/2, u = E = R.i+L.di/dt; soit t = L/R la constante de temps de la charge, il vient :
 . .
Le courant initial se calcule en écrivant que le courant est alternatif comme la tension u donc que i(0)=Io = -i(T/2). En posant  . .
La fig.4 donne l'allure de u et i.
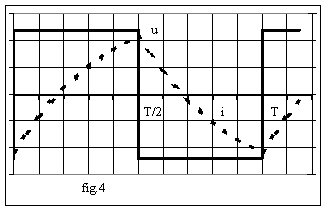
Ø méthode harmonique : on connaît la décomposition en série de Fourier de la tension u, on peut en déduire celle de l'intensité i; pour chaque harmonique de la tension
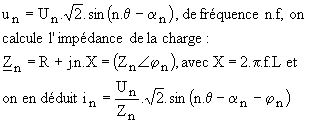
Par exemple pour un onduleur à onde rectangulaire de fréquence f = 1 kHz avec E = 24 V,
R = 12 W et L =5 mH, le tableau ci-dessous donne les résultats avec Un=2.Ö2.E/n.p, pour n impair et
yn = 0.

On peut en déduire la valeur efficace du courant I=Ö[SIn²]= 648 mA.
Ø Étude énergétique : la puissance apparente fournie à la charge est S = U.I = E.I pour une onde rectangulaire. Chaque harmonique de la tension ne peut créer de la puissance active qu'avec l'harmonique de même rang du courant :
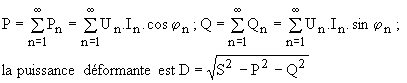
Le tableau ci-dessus donne les valeurs numériques dans l'exemple étudié. On constate que la puissance active correspond quasi totalement au fondamental.
Nous en déduisons S = 15,55 VA, P = 5,04 W ; Q = 13,72 VAR, D = 5,31 VA.
Le taux d'harmonique de la tension est de 48,3 % et celui du courant 13,1 %. La charge inductive filtre les harmoniques.
1.5 Diviseur capacitif
Le plus souvent on utilise une seule source de tension continue de valeur 2.E et un diviseur capacitif (fig.5).
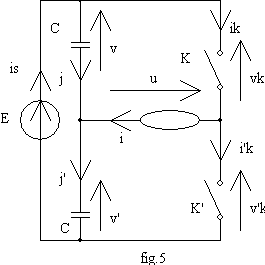
Étudions le fonctionnement pour une charge R-L.
De 0 à T/2, K est fermé et K' ouvert; les équations sont : (1) u = v = R.i+L.di/dt ; (2) v + v' = 2.E ;
(3) j + i = j' ; (4) j = C.dv/dt ; (5) j' = C'.dv'/dt ; (6) ik = i ; (7) is = j + i .
Les équations (2), (4) et (5) donnent j + j' = 0. Avec (3), nous en déduisons i = 2.j' = -2.j soit
i = -2.C.dv/dt; en reportant dans (1), il vient v + 2.R.C.dv/dt + 2.L.C.d²v/dt² = 0.
La forme canonique de l'équation est d²v/dt² +(R/L).dv/dt+v/2.L.C = 0 et l'équation caractéristique est r²+(R/L).r+1/2.L.C.
La tension v devant être quasi constante, le régime doit être apériodique, donc le déterminant de l'équation caractéristique D = (R/L)² - 2/L.C doit être positif; on doit donc avoir C > 2.L/R².
L'équation caractéristique a deux racine positives x = -R/2.L + ÖD /2 et x' = -R/2.L - ÖD /2. Le produit des racines est x.x' = 1/2.L.C > 0 et leur somme est x+x' = -R/L < 0; les deux racines sont donc négatives et la solution de l'équation est de la forme :
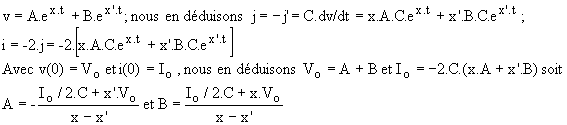
i(t) étant alternatif, i(T/2) = i(0); en posant 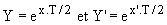 , il vient : , il vient :
(8) 2.C(x.A+x'.B)=2.C(x.A.Y+x'.B.Y').
Durant cette phase, le condensateur du haut alimente la charge donc se décharge et v diminue; pendant ce temps, le condensateur du bas se charge donc v' augmente; de T/2 à T, les rôles des condensateurs sont échangés donc celui du haut se charge. La tension moyenne par condensateur est égale à E.
En régime permanent, v(T) = v(0) = Vo et la charge perdue pendant la première phase est égale à celle gagnée durant la deuxième phase; en se référant à la tension moyenne, il vient Vo - E = E-v(T/2) soit
(9) A+B-E=E-A.Y-B.Y'.
Les équations (8) et (9) permettent de calculer A et B; les expressions ci-dessus de A et B permettent de calculer Io et Vo.
Reprenons les valeurs numériques du paragraphe 1.1.3. Pour être en régime apériodique, nous devons avoir
C > 70 µF ; prenons C = 100 µF. Le calcul donne:
x = -537 s-1, x'=-1863 s-1, A = 38,2 V, B = -13.9 V ; vo = 24,3 V , Io = -1,09 A.
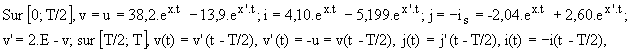
La figures 6 donne l'allure des grandeurs.
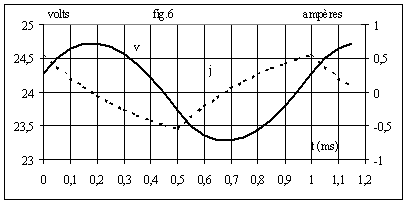
L'ondulation crête à crête de la tension v est de 1,45 V soit 6% de sa valeur moyenne E.
2 Structure avec trannsformateur à point milieu
Le montage est donné sur la fig.8 : 
Le transformateur est supposé parfait; chaque demi primaire a n1 spires et le secondaire a n2 spires; nous en déduisons, en posant m = n2/n1, v = v' et u = m.v , ik-i'k = m.i.
De 0 à T/2, K est fermé et K' ouvert; nous en déduisons vk=0 donc v = E et u = m.E; v' = E donc
v'k = 2.E; i'k = 0 donc ik = m.i.
De T/2 à T, K est ouvert et K' fermé; v'k =0 donc v' = v = -E et vk = 2.E; ik = 0 donc i'k = -m.i.
Les grandeurs ont la même allure que pour l'onduleur en demi-pont, seules les amplitudes diffèrent :
v u est un créneau symétrique d'amplitude m.E
v l'intensité ik est égale à m.i de 0 à T/2 et à 0 de T/2 à T
v le courant dans la source de tension est égal à m.i de 0 à T/2 et à -m.i de T/2 à T. Sa valeur moyenne est le double de celle calculée pour l'onduleur en demi-pont soit 2.m.Imax.cosj/p.
v la tension est égale à 2.E aux bornes de K ou K' lorsqu'ils sont bloqués.
Le calcul réel du courant et le choix des interrupteurs se fait comme pour le montage en demi-pont.
3 structure en pont
3.1 Étude structurelle
Quatre interrupteurs identiques sont connectés en pont. Chaque interrupteur est formé par un interrupteur unidirectionnel commandé K et une diode tête-bêche.
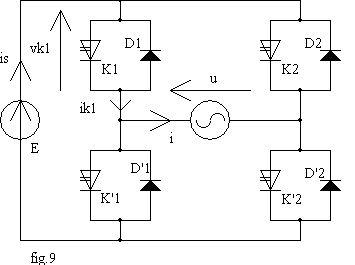
Les règles de structure imposent que les interrupteurs d'un même bras, K1 et K'1 d'une part, K2 et K'2 d'autre part aient des états complémentaires.
Chaque interrupteur sera donc fermé sur une demie période.
Pour obtenir une onde à deux niveaux, K1 et K'2 sont fermés de 0 à T/2 , K'1 et K2 de T/2 à T.
Pour obtenir une onde à trois niveaux, on décale les commandes des deux bras d'un angle a : K1 et fermé de 0 à p et K'1 de p à 2.p; K'2 est fermé de a à p+a et K2 de p +a à 2.p +a.
Dans ce cas, les formes d'onde sont données sur la fig.10 pour une branche courant de type inductif.

Lorsque K1 et K2 , ou K'1 et K'2, conduisent u = 0 et is = 0; lorsque K1 et K2 conduisent u = E et is = i. Lorsque K'1 et K2 conduisent u = -E et is = - i.
Lorsqu'un interrupteur est commandé à la fermeture, K ou D conduit suivant le signe de i et la place de l'interrupteur : pour K1 et K'2, K conduit pour i > 0 et D pour i < 0; pour K'1 et K2, K conduit pour i < 0 et D pour i > 0.
3.2 Calcul du courant i pour une charge R - L
Calcul direct
Ø de 0 à a, u = 0 = R.i+L.di/dt; si on utilise la variable angulaire q = w.t, il vient R.i+X.di/dq = 0 avec
X = L.w; en posant k = X/R, la solution est de la forme :
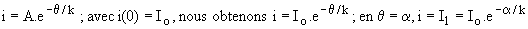
Ø de a à p, u = E = R.i+X.di/dq;

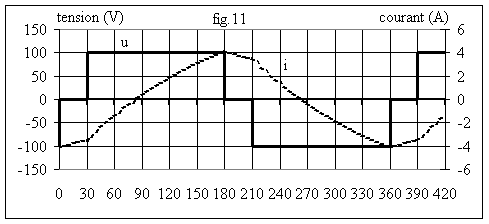
Faisons une application numérique avec E = 100 V ; R = 10 W ; L = 5 mH ; f = 1 kHz et a = 30°.
Nous en déduisons X = 31,42 W ; k = 3,14 ; Io = -4.13 A ; I1 = -3,50 A.
La fig.11 donne l'allure des graphes de u et de i.
Calcul harmonique
Nous avons calculé au Chapitre 7.1, paragraphe 5.2 les harmoniques de la tension u:


Si nous reprenons l'exemple numérique du paragraphe 3.2.1, nous obtenons les résultats du tableau ci-dessous :
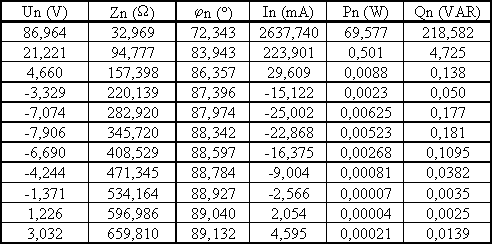
Nous en déduisons U = 91,3 V ; I = 2,65 A ; P = 70,1 W ; Q = 224 VAR ; S = 242 VA ; D = 57,6 VA ;
Fp = 0,29 alors que la facteur de puissance de la charge en régime sinusoïdal est de 0,3.
Le taux d'harmoniques de la tension est tHu = 31,9 % et celui du courant tHi = 8,71 %.
4 structure à résonance série
La charge est un dipôle R-L-C série : 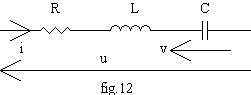
L'onduleur en pont ou en demi-pont fonctionne en onde rectangulaire deux niveaux : de 0 à T/2 u = E et de T/2 à T u = - E.
Calcul direct des grandeurs
Les équations de la charge sont : u = R.i + L.di/dt + v , i = C.dv/dt ; nous en déduisons L.C.d²v/dt² + R.C.dv/dt + v = u . Sur [0 ; T/2], L.C.d²v/dt² + R.C.dv/dt + v = E

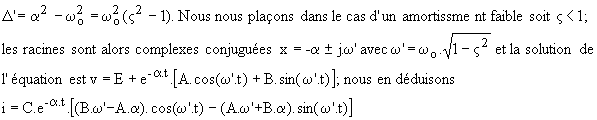
Les conditions initiales v(0) = vo et i(0) = Io donnent :

Faisons une application numérique : E = 100 V ; R = 25 W ; L = 5 mH ; C = 820 nF.
Nous calculons a = 2 500 s-1 , wo = 15 617 rd/s correspondant à une fréquence de résonance fo = 2 486 Hz ,
z = 0,16 , w' = 15 416 rd/s .
Commandons l'onduleur à diverses fréquences :
Ø f = 2 kHz : nous calculons Io = 1,91 A ; vo = -174 V ; A = -274 V et B = 106 V; la fig.13 donne l'allure de i et de v. La charge étant capacitive à la fréquence f, le courant i est positif en t = 0
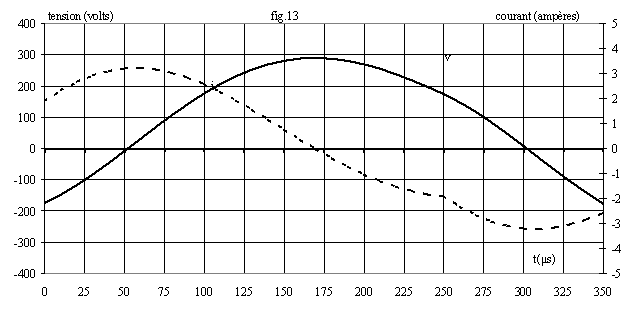
Ø f = fo : nous calculons Io = -0,4 A ; vo = -398 V ; A = -498 V et B = -113 V; la fig.14 donne l'allure de i et de v. Le courant est quasi nul en t = 0.
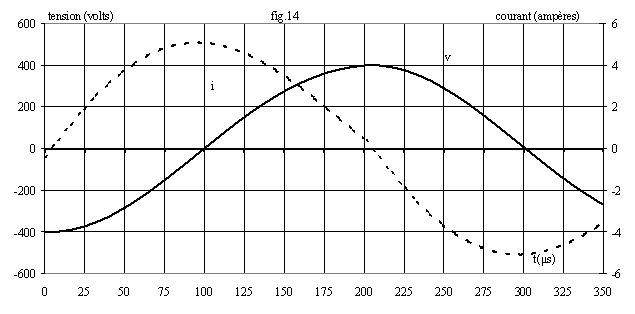
Ø f = 3 kHz : nous calculons Io = -2,84 A ; vo = -138 V ; A = -238 V et B = -263 V; la fig.15 donne l'allure de i et de v. La charge étant inductive, le courant est négatif en t = 0.
4.2 Choix des interrupteurs
Chaque interrupteur conduit sur une demie période, le courant changeant de signe sur cet intervalle. A cet instant il y a commutation de la diode D à l'interrupteur commandé K ou l'inverse; cette commutation est naturellement douce puisque i = 0.
Ø si la fréquence de commande f est inférieure à la fréquence, le circuit est globalement capacitif et i(0) > 0. K conduit en 0+; sa fermeture doit être commandée; son blocage est naturel par annulation du courant; ce mode de fonctionnement convient parfaitement pour des thyristors.
Ø si la fréquence de commande f est supérieure à celle de résonance, i(0) < 0. D conduit en 0+ et K en T/2; l'ouverture de K doit être commandée; ce fonctionnement correspond à celui du thyristor dual.
Ø si la fréquence est proche de la résonance, toutes les commutations se font à courant quasi nul; on a donc commutation douce.
Dans tous les cas, ce type d'onduleur réduit les pertes de commutation donc peut fonctionner à fréquence élevée
4.3 Approximation du premier harmonique
Lorsque le coefficient d'amortissement z << 1 et la fréquence de commande peu différente de la fréquence propre du circuit résonant, le courant i est peu différent de son terme fondamental. Étudions le fonctionnement dans cette hypothèse dite du premier harmonique.
Le fondamental de la tension de fréquence f est :

 . .
Si nous fixons E, L, C et la fréquence de commande f, U1 et Icc sont fixés; lorsque R varie, le graphe Vr1(I1) correspond à un quart d'ellipse correspondant à l'équation ci-dessus. Comme on a de plus Vr1 = R.I1 (droite de charge), l'intersection de l'ellipse avec la droite de charge donne le point de fonctionnement donc Vr1, I1 et P.
Si nous fixons E, L, C et R, pour une valeur de f donc de x, l'intersection de l'ellipse avec la droite de charge donne le point de fonctionnement.
Remarquons que le résultat est le même pour deux valeurs de la fréquence f1 et f2 telles que f1/fo = fo/f2 soit
x1 = 1/x2; si x1 > 1, le circuit est inductif à cette fréquence ; on a alors x2 <1 donc un circuit capacitif. Le choix de x > 1 ou x < 1 se fait en fonction des interrupteurs utilisés.
La fig.16 donne les graphes pour E = 100 V , L = 5 mH ; C = 820 nF, et trois valeurs de x :1,01 ; 1,02 et 1,04.
On a également tracé deux droites de charges pour R = 5 W et R = 2,5 W.

Dans les mêmes conditions, on a tracé fig.17 les graphes P(I1) et les droites de puissances P = R.I1².
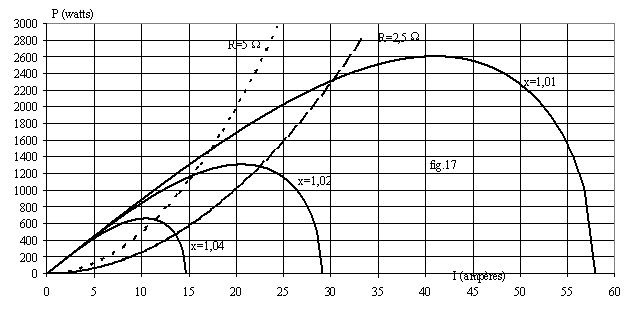
Ø Pour x =1,01 soit f = 2 510 Hz, si R varie de 5 à 2,5 W , la tension varie de 86 à 76,5 V et la puissance de 1 500 W à 2 300 W.
Ø Pour R = 2,5 W, si x varie de 1,01 à 1,04, la tension varie de 76,5 à 35 V et la puissance de 2 300 à 480 W.
On peut donc régler la puissance transmise à la charge en jouant sur la fréquence de commande.
Pour x fixé, la puissance est maximale pour I = Icc/Ö2 et vaut U1.Icc/2.
Notons que, sur le graphe de puissance, le point d'intersection de P(I1) avec la parabole P = R.I1² doit se situer dans la partie croissante du graphe.
En effet dans cette partie, l'augmentation de R fait chuter la puissance alors que dans la partie décroissante, l'augmentation de la résistance fait augmenter la puissance.
Or au cours du fonctionnement, la puissance dissipée dans R augmente sa température donc sa résistance. Si l'augmentation de R produit une augmentation de puissance, la température augmente encore et l'effet cumulatif conduit le système à fonctionner de façon instable.
Seules les valeurs de P < Pmax correspondent donc à des points de fonctionnement stables.
5 filtre d'entrée
Il est le plus souvent nécessaire de placer un filtre de type L - C entre la source de tension et l'onduleur. La source présente toujours une inductance parasite, or le courant source présente une discontinuité à chaque commutation dans l'onduleur; le condensateur C permettra cette discontinuité tout en lissant la tension appliquée à l'onduleur. L'inductance L réduit l'ondulation du courant dans la source afin de limiter les pertes.
Étudions le comportement de ce filtre pour un onduleur en pont, en supposant le courant charge sinusoïdal et les interrupteurs parfaits (fig.20).
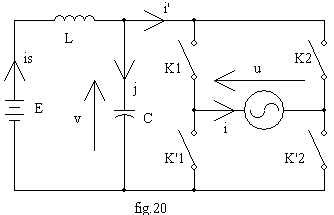
On a E = v+L.dis/dt et j = C.dv/dt = is - i'.
Si l'onduleur est commandé à la fréquence f = w/2.p avec un décalage angulaire a , on a :
v 0 < w.t < a : K1 et K2 fermés donc u = 0 et i' = 0
v a < w.t < p : K1 et K'2 fermés donc u = v et i' = i = Imax.cos(w.t-j).
v p < w.t < p+a : K'1 et K'2 fermés donc u = 0 et i' = 0
v p+a < w.t< 2.p+a : K'1 et K2 fermés donc u = -v et i' = -i = -Imax.cos(w.t-j).
Comme i(t+T/2) = -i(t), les grandeurs du filtre sont de période T/2.
6.1 Calcul du condensateur
Négligeons pour ce calcul l'ondulation du courant source is.


La fig.21 donne l'allure de v/E pour a = Cste et j variable, la fig.22 pour a variable et j constant.


L'ondulation de la tension v est maximale pour a = 0° et j = 90°; dans ce cas la valeur moyenne de is est nulle :
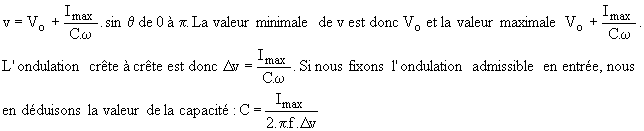
6.2 Calcul de l'inductance
La valeur de l'intensité dans la source se déduit de celle de la tension v par l'équation L.dis/dt = E-v. En remplaçant v par l'expression calculée au paragraphe ci-dessus, on peut déterminer is par intégration; la constante d'intégration se calcule à partir de la valeur moyenne Is.
L'ondulation du courant est maximale lorsque celle de la tension v est maximale, c'est à dire pour a = 0° et
j = 90°; nous avons alors 
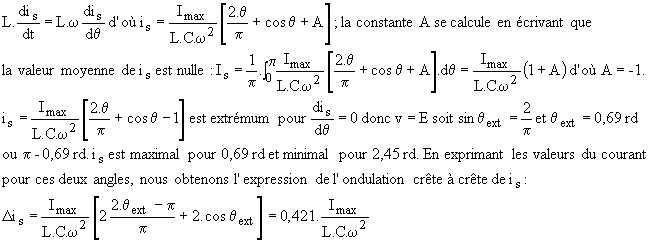
Si on fixe l'ondulation de la tension v et celle du courant source, on peut donc calculer les composants du filtre :

6 choix d'une structure et de son mode de commande
Les onduleurs de tension monophasés sont les plus souvent utilisés pour des puissances faibles à moyennes.
On distingue deux types d'applications :
Ø les onduleurs alimentés sur batterie donc en basse tension; ces onduleurs nécessitent généralement l'emploi d'un transformateur pour alimenter la charge sous une tension suffisante.
Ø les onduleurs alimentés à partir du réseau à travers un redresseur.
Pour régler la puissance transférée à la charge, on peut utiliser :
Ø le décalage des commandes dans les onduleurs en pont
Ø le réglage par la fréquence dans les onduleurs à résonance
Ø la modulation de largeur d'impulsions
Envisageons les avantages et inconvénients des structures :
Ø onduleur en demi-pont à onde rectangulaire :
v avantages
· structure simple et économique avec seulement deux interrupteurs commandés et deux diodes.
· un seul interrupteur passant à chaque instant donc chute de tension réduite
· les condensateurs du diviseur capacitif peuvent servir pour le filtrage en entrée et/ou pour la résonance série
v inconvénients
· la tension de blocage des interrupteurs est 2.E soit deux fois la tension maximale aux bornes de la charge.
· le réglage de la puissance ne peut se faire que par modulation de largeur d'impulsions; la fréquence de commutation est alors de 6 à 10 fois celle du fondamental du courant charge; les pertes de commutation sont augmentées. La durée de chaque créneau doit être grande devant les temps de commutation, ce qui limite la fréquence de l'onduleur.
Ce type d'onduleur est le plus souvent utilisé pour l'alimentation en basse tension.
Ø onduleur en pont
· la tension de blocage de chaque interrupteur est égale à la tension maximale aux bornes de la charge
· la commande à décalage permet de régler la puissance fournie sans augmenter la fréquence de commutation
· la commande MLI trois niveaux (-E, 0 ,E) est possible ce qui permet de réduire les harmoniques
· nécessite quatre interrupteurs commandés et quatre diodes
· à chaque instant, la charge est alimentée à travers deux interrupteurs en série ce qui crée une chute de tension de 1,5 à 3 volts.
Ce type d'onduleur est surtout utilisé en haute tension et dans les montages à commande en modulation de largeur d'impulsion.
Ø onduleur avec transformateur à point milieu
v avantages :
· structure simple et économique avec seulement deux interrupteurs commandés et deux diodes.
· un seul interrupteur passant à chaque instant donc chute de tension réduite
· le transformateur permettant d'élever la tension charge est inclus dans la structure
v inconvénients :
· à chaque instant, un seul demi primaire est utilisé ce qui oblige à surdimensionner le transformateur d'environ 40 % par rapport à la puissance fournie à la charge.
· les harmoniques de la tension induisent des pertes supplémentaires dans le fer
v avantages :
· réduction des pertes de commutation donc possibilité de travailler à fréquence élevée
· réglage de la puissance par variation de la fréquence
· le condensateur en série interdit la circulation d'une composante continue du courant charge en cas de décalage des temps de conduction des interrupteurs d'un bras; ceci est important lorsqu'un transformateur est utilisé car la composante continue risque de saturer le circuit magnétique
· fonctionnement de la charge en régime quasi sinusoïdal donc pas besoin de filtre de sortie et pertes réduites pour l'utilisation d'un transformateur
v inconvénients :
· la puissance fournie à la charge varie rapidement avec la fréquence de commande et l'amortissement du circuit résonant.
|