Électronique de puissance
xxxxModule 7 : xxxx "Conversion DC - AC " |
Chapitre 7.2
Onduleurs monophasés de tension |
|
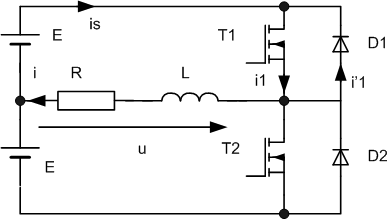
On étudie le montage ci-dessous :
on donne : è la tension d'alimentation E = 48 V è les composants de la charge : R = 15 W et L = 10 mH Les transistors sont commandés à la fréquence f = 400 Hz; T1 est fermé de 0 à T/2 et T2 de T/2 à T. |
||
1.1 |
En utilisant le calcul direct, donner l'expression du courant i dans la charge | u = E = R.i+L.di/dt; avec t = L/R = 667 µs, il vient : le courant est alternatif donc que i(0)=Io = -i(T/2). En posant |
1.2 |
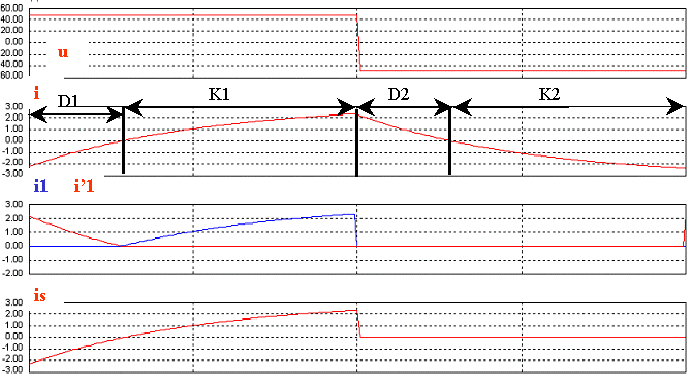
Tracer les graphes de la tension u et des intensités i, is, i1 et i'1 ; indiquer les intervalles de conduction des quatre interrupteurs |
|
1.3 |
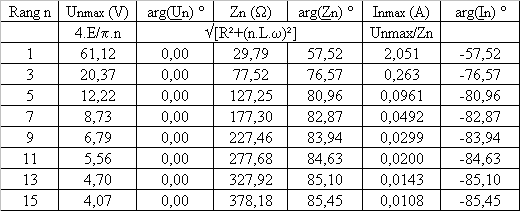
Calculer les harmoniques de la tension u et du courant i jusqu'au rang 15 |
|
1.4 |
Calculer le taux global d'harmoniques du courant i | th =Ö[(I3² +I5² +I7² +...)/I1² ] = 14 % |
1.5 |
Calculer la valeur efficace de i et en déduire la puissance active absorbée par la charge | I =Ö[(I1max²+ I3max² +I5max² +I7max² +...)/2 ] = 1,46 A P = R. I² = 32,2 W |
1.6 |
Calculer la valeur moyenne du courant is | Les pertes dans l'onduleur étant négligées, la puissance fournie par les deux sources est égale à la puissance dans la charge. Comme les deux sources fonctionnent de façon symétrique sur chaque demie période, il vient 2.E.Ismoy = P soit Ismoy = 0,34 A |
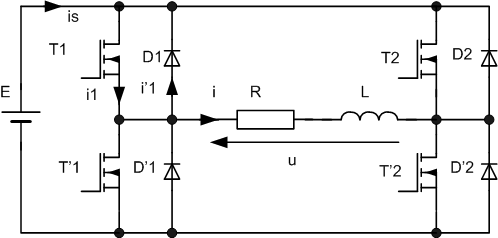
On utilise la structure en onduleur trois niveaux en décalant la commande des deux bras de T/12 |
||
2.1 |
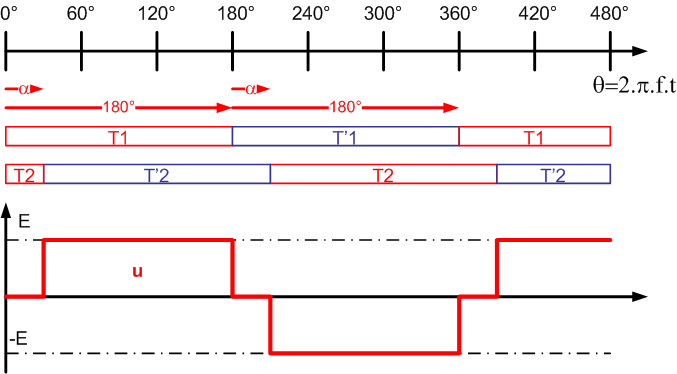
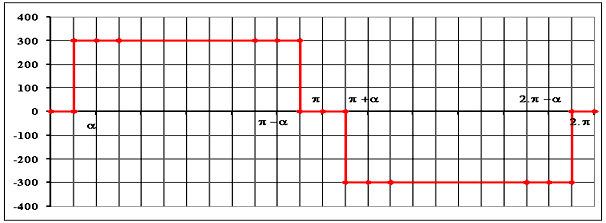
En utilisant la variable q = 2.p.f.t, représenter les intervalles de fermeture des 4 transistors; en déduire le graphe de la tension u(q) |
|
2.2 |
Calculer la valeur efficace de u(q) | U=E.Ö[(p-a)/p] avec a = 360/12 = 30° , U = 274 V |
2.3 |
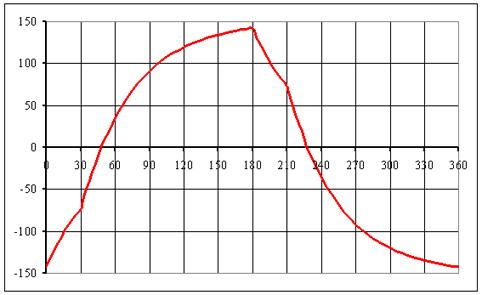
Déterminer l'expression du courant i(q); tracer son graphe | De 0 à a, u = 0 = R.i+L.di/dt; si on utilise la variable angulaire q = w.t, il vient R.i+X.di/dq = 0 avec X = L.w = et 1,57 W et k = X/R= 0,785 , la solution est I = Io.exp(-q/k) En q = a, i(a) = I1 = Io.exp(-a/k) De a à p, u = E = R.i+X.di/dq; I = B .exp(-q/k) + E/R i étant continu en q = a, i = (I1- E/R) exp[(q -a)/k] + E/R En q = p, i(p) = I2 = (I1- E/R) exp[(p -a)/k] + E/R Le courant étant alternatif i(p) = -i(0) ; nous en déduisons Io = -(E/R). exp[(p -a)/k] / exp(-p/k) = -142 A
|
2.4 |
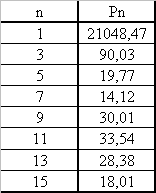
Calculer les harmoniques de u et i jusqu'au rang 15 | Chaque harmonique de la tension ne crée de la puissance qu'avec l'harmonique de même rang du courant : Pn = Uneff.Ineff.cosjn
On a P = SPn = 21,28 kW soit quasiment la puissance du fondamental |
2.5 |
Calculer la puissance active fournie à la charge | Il n'y a que des harmoniques impairs : un = Unmax.sin(nq) avec Unmax = (4.E/p.n).cos(n.a/2) Zn = (Zn ; jn) = R + j.n.L.w in = I nmax.sin(nq - jn) avec Inmax = Unmax / Zn
|
On utilise une commande MLI obtenue par une modulation sinus-triangle. La fréquence du triangle est p.f = 1 kHz |
||
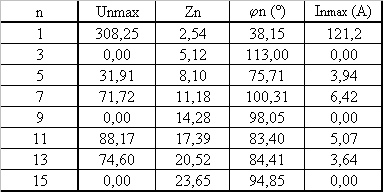
2.6 |
On veut que la valeur efficace du terme fondamental du courant soit If = 60 A. Quelle doit être la valeur maximale du terme fondamental de la tension ? | L'impédance à la fréquence f = 50 Hz est de module Z1 = 2,54 W; il faut donc une valeur efficace du fondamental Uf = Z1.If = 153 V |
2.7 |
Pour obtenir ce fonctionnement, quelle doit être la valeur du rapport m = amplitude sinus / amplitude triangle |
Uf = 153 V donne une valeur maximale 153. Ö2 = 216 V Pour une fréquence de modulation p.f avec p > 5, l'amplitude du fondamental est m.E, il faut donc m = 216 / 300 = 0,72 |
2.8 |
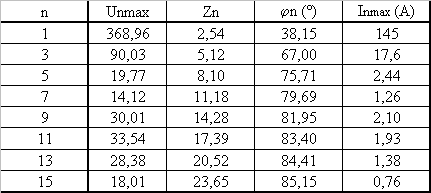
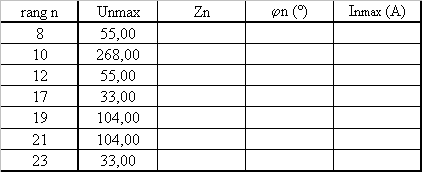
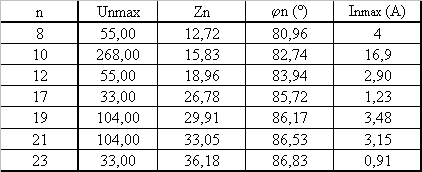
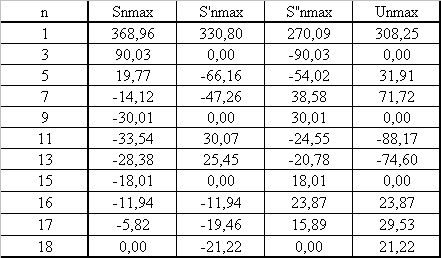
Pour calculer les harmoniques du courant, compléter le tableau ci-dessous
|
|
2.9 |
Que peut-on dire de la valeur efficace du courant i ? | L'harmonique le plus grand est de valeur maximale 17 A donc de valeur efficace 12 A soit 5 fois moins que le fondamental; on peut donc dire que I est peu diffréent de If = 60 A |
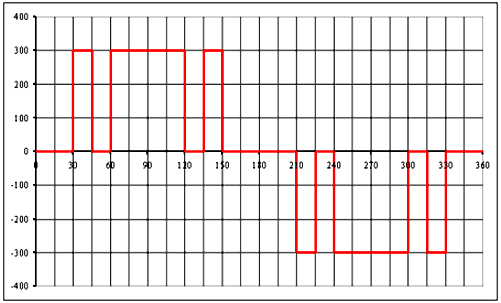
On utilise une commande MLI calculée. La fonction de base est représentée ci-dessous :
On utilise trois signaux de ce type s défini par a = 15°, s' défini par a' = 30° et s" défini par a" = 45°. Ces signaux sont de fréquence f = 50 Hz. La commande est telle que u = s - s' + s". |
||
2.10 |
Représenter la tension u(q) et calculer sa valeur efficace |
U = E. Ö{[2.(a' -a) + (p-2.a")]/p} = 245 V |
2.11 |
La fonction de base n'a que des harmoniques impairs de forme (4.E/p.n).cos(n.a).sin(n.q). Calculer l'amplitude des harmoniques de s, s' et s"; en déduire celle des harmoniques de u |
Les harmoniques sont tous en phase ou en opposition de phase donc Unmax = Snmax - S'nmax + S"nmax |
2.12 |
Calculer l'amplitude des harmoniques du courant i; en déduire sa valeur efficace |
I = 86 A |
On alimente la charge par une source sinusoïdale de valeur efficace V et de fréquence f = 5 kHz |
||
3.1 |
Calculer la tension V pour avoir un courant efficace I = 1 000 A |
Z = R + j.Lw = 0,04 + j.0,471 Z = (0,472 W ; 85,1°) V = Z.I = 472 V |
3.2 |
On dispose d'une source V = 230 V; pour obtenir I = 1 000 A, on place en série avec la charge un condensateur de capacité C. Calculer l'impédance que doit avoir le circuit R - L - C | L'impédance de la charge doit être de mdoule Z' = Z = V / I = 0,23 W
|
3.3 |
Montrer qu'il existe deux valeurs possibles de C que l'on calculera | Z = R + j.(L.w - 1/C.w) = R + j.X' ; X' ²= Z' ² - R ² ; on a deux solutions possibles X'1 = 0,226 W qui correspond à C1 = 1/w.(L.w-X'1) = 131 µF et X'2 = -0,226 W qui correspond à C2 = 1/w.(L.w-X'2) = 45,6 µF |
3.4 |
Quelle valeur de C doit-ton choisir pour que le courant soit en avance sur la tension? | Pour avoir un courant en avance sur la tension, il faut une réactance X' < 0 ; la capacité du condensateur vaudra donc 45,6 µF |
On alimente la charge R - L - C définie ci-dessus par l'onduleur avec E = 100 V et f = 5 kHz |
||
3.5 |
Quelle est la valeur fo de la fréquence de résonnance ? | fo = 1 /2.p.Ö(L.C) = 6,08 kHz |
3.6 |
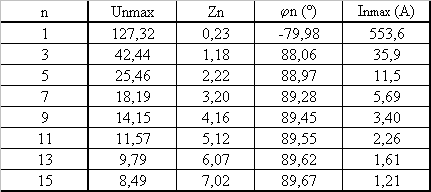
Calculer les harmoniques de la tension u et du courant i |
|
3.7 |
Montrer que l'on peut appliquer la méthode du premier harmonique | Le fondamental du courant est 15,4 fois plus grand que l'harmonique 3, On peut donc négliger ces harmoniques dans le calcul des valeurs efficaces et des puissances |
3.8 |
Quelle doit être la valeur de la fréquence pour avoir un courant de valeur efficace I = 1 000 A ? |
La valeur efficace du fondamental de u est 127,3 / Ö2 = 90 V; il faut donc une impédance de module Z = Ö(R² + X'²) = 90 mW soit X = - 80,6 mW ou X = 80,6 mW X' = L.w - 1/C.w donne L.C.w² -X'.C.w - 1 = 0 avec les deux valeurs de X' on a deux solutions positives ( une dans chaque cas) : 35 644 rd/s soit 5 676 Hz et 41 017 rd/s soit 6 528 Hz. Si on veut garder un courant en avance sur la tension, on choisira 5 676 Hz |