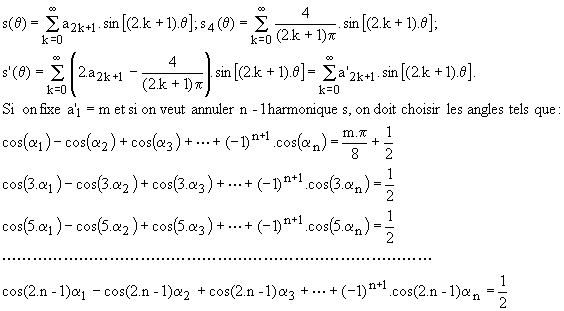Commande adjacente : onduleur à deux niveaux
è Valeur efficace : Y = Yo = Cste imposée par la source
è Harmoniques : 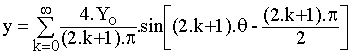
Commande adjacente : onduleur à deux niveaux

è Valeur efficace : Y = Yo = Cste imposée par la source
è Harmoniques : 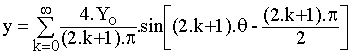

Commande décalée : onduleurs à trois niveaux
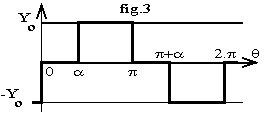
è Valeur efficace : Y=Yo.Ö[(p-a)/p], valeur variable avec le décalage de commande a.
è Harmoniques : 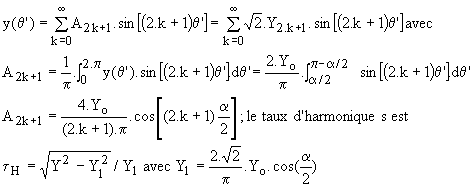
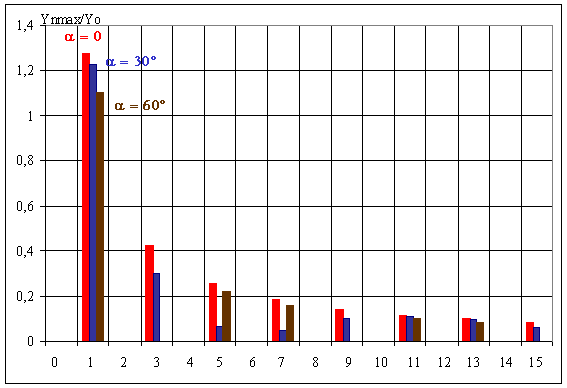
Le réglage du décalage a permet de :
v régler la valeur efficace Y
v d'agir sur les harmoniques
MLI intersective ou sinus-triangle
Comparer un sinus d'amplitude m et de fréquence f avec un triangle d'amplitude 1 et de fréquence p.f
è Valeur efficace Y = Yo
è Fondamental : si p > 5 on a un fondamental d'amplitude
Y1 = m.Yo
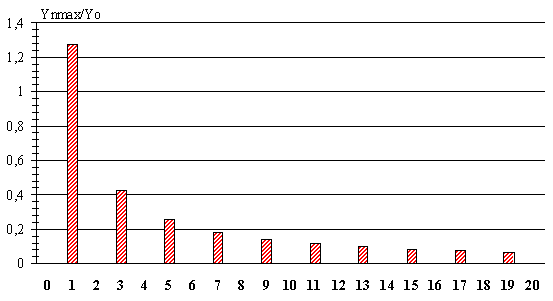
è Harmoniques : on a un fondamental à la fréquence f de la sinusoïde et des paquets d'harmoniques autour des fréquences k.p.f multiples de celle du triangle
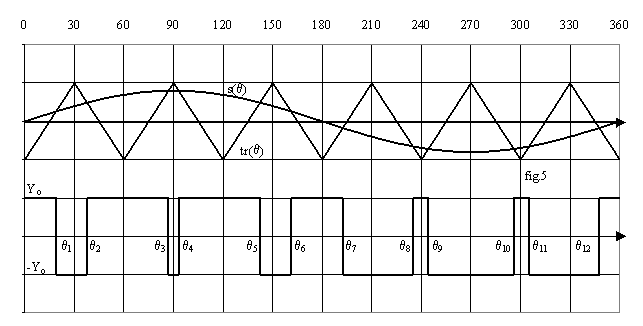
MLI calculée
On calcule les angles pour lesquels la tension change de niveau afin de régler la valeur efficace du fondamental et d'éliminer certains harmoniques
è Trois niveaux :
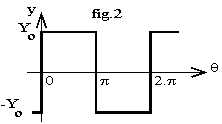
L'onde modulée est y(q) = Yo.s(q) avec ![]() (fig.9 pour n = 3).
(fig.9 pour n = 3).
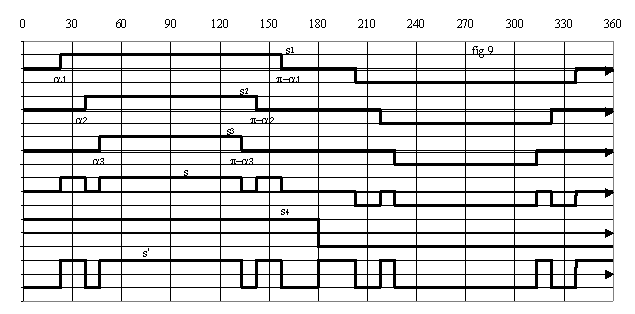
La décomposition en série de Fourier donne :
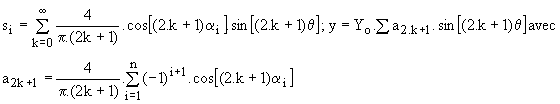
Si nous voulons fixer la valeur du fondamental Y1max=Yo.a1 et annuler les harmoniques de rang 3, 5, 7, …, 2.n-1, nous devons choisir les angles de découpage tels que
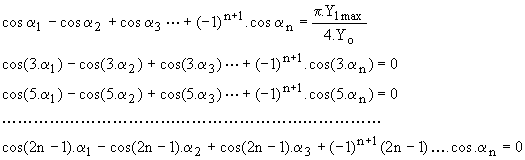
è Onduleur à deux niveaux :
si on réalise la somme s' = 2.s + s4, s étant le signal étudié ci-dessus et s4 un créneau symétrique, nous obtenons un signal 2 niveaux ( +1 et -1) à modulation calculée (fig.9). Nous avons :