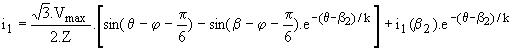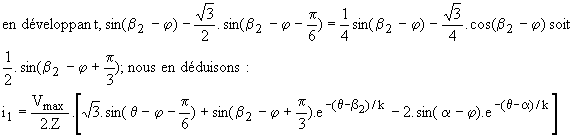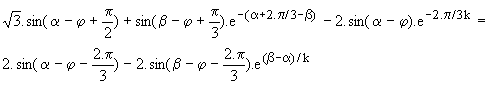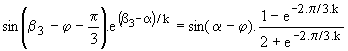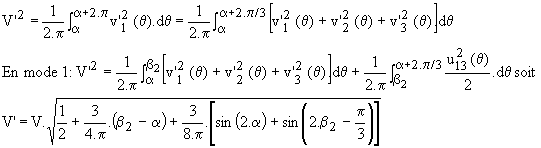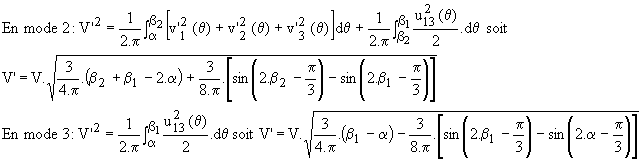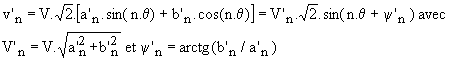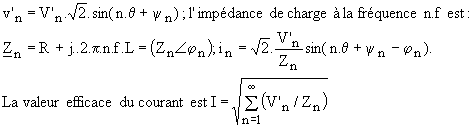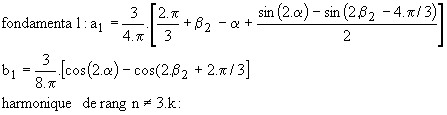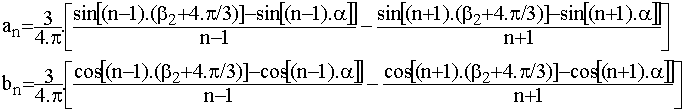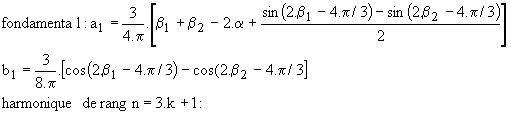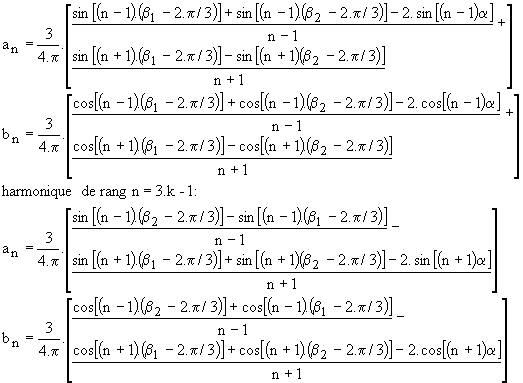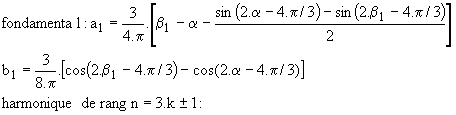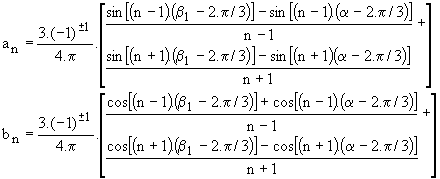Diverses structures sont utilisées suivant le couplage de la charge, le couplage des interrupteurs, le choix des interrupteurs … Parmi les structures les plus utilisées, citons :
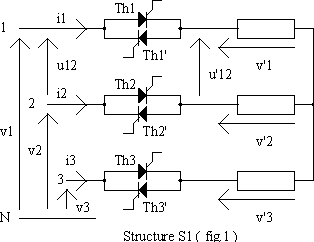
Ø La structure S1 (fig.1) comporte une charge équilibrée couplé en étoile avec deux thyristors tête-bêche par phase.
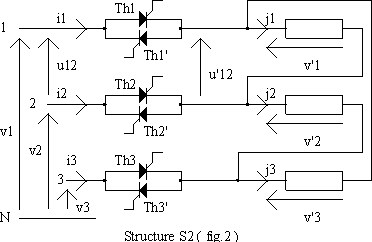
Ø La structure S2 (fig.2) comporte une charge équilibrée couplé en triangle avec deux thyristors tête-bêche par phase.
Ø La structure S3 (fig.3) est formée des trois gradateurs monophasés couplés en triangle.

Ø La structure S4 dite "économique" (fig.4) dérivée de la structure S1 en supprimant les thyristors de la phase 3.
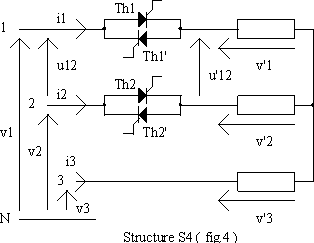
On trouve également des structures mixtes, obtenues avec les structures S1, S2 ou S3 en remplaçant les thyristors Th1', Th2' et Th3' par trois diodes.
2 étude de la structure S1
2.1 Principes
Le thyristor Th1 est commandé avec un retard a par rapport au passage à zéro de la tension simple v1.Le thyristor Th'1 est commandé en p+a. Les thyristors de la phase 2 sont commandés avec un retard de 120° sur ceux de la phase 1 et ceux de la phase 3 avec un retard de 240° sur ceux de la phase 1.
Les tensions et courants dans les phases de la charge doivent être alternatives et triphasées.
On a donc : 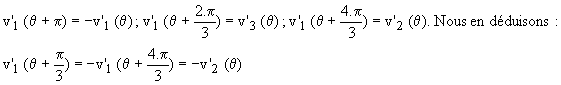
Il en est de même pour les autres phases en permutant circulairement les indices 1, 2 et 3.
Nous en déduisons qu'il suffit d'étudier les formes d'onde sur un intervalle égal à p/3 pour connaître le fonctionnement sur une période.
Notons que si le fil neutre est connecté, chaque phase fonctionne comme un gradateur monophasé indépendamment des deux autres phases; l'étude de chaque phase est identique à celle faite au chapitre 30. La connexion du fil neutre permet le fonctionnement sur charge déséquilibrée.
2.2 Analyse pour une charge R
La charge est formée de trois résistances R identiques. Dans ce cas, chaque thyristor se bloque lorsque le courant donc la tension v' de la phase passe par 0.
L'ordre de commande des thyristors est : Th1 en a, Th3' en a+60°, Th2 en a+120°, Th1' en a+180°, Th3 en a+240° et Th2' en a+300°.
D'après le résultat du paragraphe 1, nous étudions la structure pour a £ q £ a+p/3.
Nous devons avoir à chaque instant i1+i2+i3 = 0; de plus un seul thyristor peut être passant dans chaque phase : quand Th1 conduit, Th1' est polarisé sous une légère tension négative donc ne peut être commandé.
Si un Th1 conduit, i1 > 0 donc i2+i3 < 0, donc Th2' ou Th3' conduit.
Les régimes de conductions possibles sont :
v les six thyristors sont bloqués : i1= i2 = i3 = 0.
v deux thyristors sont passants simultanément, nécessairement un parmi Th1, Th2 et Th3 et un parmi Th1', Th2' et Th3'.
v trois thyristors sont passants simultanément : deux parmi Th1, Th2 et Th3 et un parmi Th1', Th2' et Th3' ou un parmi Th1, Th2 et Th3 et deux parmi Th1', Th2' et Th3'.
v Envisageons le cas où Th1 et Th2' conduisent seuls; on a donc i3 = 0 et i1+i2 = 0;
v'1 - v'2 = u12 = R( i1-i2) = 2.R.i1 donc i1 = u12 /2.R Ceci n'est possible que si i1 > 0 donc u12 > 0; sur l'intervalle 0 £ q £ 360°, cette inégalité est vérifiée pour 0 £ q £ 150°.
C'est la seule combinaison possible avec deux thyristors passants puisque Th3' est amorcé 60° après Th1.
v Envisageons le cas où Th1, Th2' et Th3 conduisent ; dans ce cas la charge est directement connectée au réseau triphasé et v'n = vn = R.in pour n = 1, 2 et 3. Nous devons avoir simultanément
v1 > 0 , v2 < 0 et v3 > 0. Ceci impose 0 £ q £ 60°. Compte tenu de l'ordre d'amorçage, c'est la seul combinaison possible comprenant Th1.
Ø Mode 1 = 2 ou 3 thyristors passants : si a = 0, la charge est en permanence connectée au réseau donc v'1 = v1, v'2 = v2 et v'3 = v3. A l'amorçage de Th1, Th2' et Th3 conduisent; Th2' se bloque pour v2 = 0 soit
q = 120° et Th3 pour v3 = 0 soit q = 60°. Th3 se bloque donc en 60°, instant d'amorçage de Th3'. Lorsque a augmente, Th1, Th2' et Th3' conduisent en a si a £ 60°.
Th3 se bloque toujours en q = 60° donc avant l'amorçage de Th3' en a +60°. On aura donc successivement Th1, Th2', Th3 passants de a à 60° avec v'1 = v1, puis de 60° à a+60°, Th1 et Th2' passants avec v'1 = u12 /2.
Le mode 1 n'est possible que si 0 £ a £ 60°
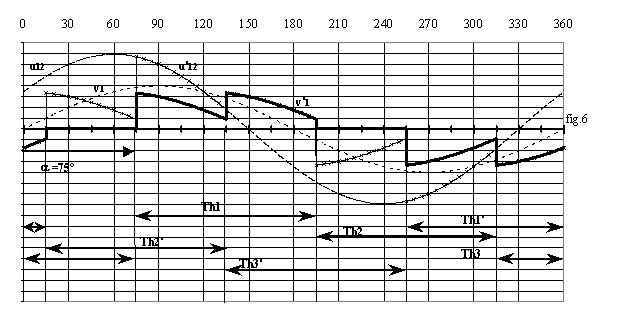
Ø Mode 2 = 2 thyristors passants : si a est supérieur à 60°, Th1, Th2' et Th3 ne peuvent conduire simultanément. A l'amorçage de Th1, on aura Th1 et Th2' passants soit v'1 = u12 /2. Ceci suppose que
u12 > 0 donc q < 150° . Th2' doit conduire jusqu'à l'amorçage de Th3' en a+60°; il faut donc a+60° < 150° soit a < 90°.
Le mode 2 n'est possible que si 60 £ a £ 90°
Ø Mode 3 = 0 ou 2 thyristors passants : si a > 90°, Th2' se bloque en 150° avant amorçage de Th3'; comme Th1 ne peut conduire seul, tous les thyristors sont bloqués de 150° à a+60°. A cet instant, on amorce Th3' et il faudra réamorcer Th1 pour pouvoir avoir de nouveau conduction.
Pour que Th1 et Th2' puissent conduire, il faut u12 > 0 donc q < 150°; si a > 150°, aucune conduction ne sera possible.
Le mode 3 n'est possible que si 90 £ a £ 150°
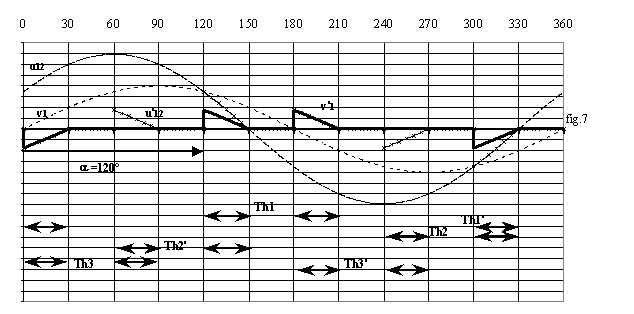
2.3 Analyse pour une charge R - L
La charge est formée par une résistance R en série avec une inductance L. On pose 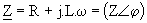 . .
L'inductance L interdit toute discontinuité du courant en ligne; chaque thyristor se bloque naturellement par annulation du courant qui le traverse; le courant i1 étant en retard sur la tension v'1, celle-ci est négative au moment du blocage de Th1.
Le mode 2 avec deux thyristors passants en permanence ne peut plus exister; en effet si Th3 et Th2' conduisent au moment de l'amorçage de Th1, en q = a, i1 = 0, i2 < 0 et i3 >0; aucun de ces courants ne pouvant être discontinu, les trois thyristors conduisent donc on est en mode 1.
Quand a diminue, on passe directement du mode 3 au mode 1.
Ø Mode 3 = 0 ou deux thyristors passants : lors de l'amorçage de Th1 en q = a, tous les thyristors sont bloqués en mode 3, donc tous les courants sont nuls. Il faut réamorcer Th2' pour pouvoir avoir conduction. Pour q > a, Th1 et Th2' conduisent donc i1 = -i2 , v'1 = -v'2; u'12 = u12 = v'1 -v'2 donc v'1 = u12/2.
En posant X = L.w, il vient :
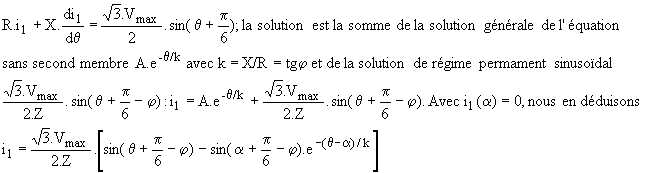
Les deux thyristors se bloquent pour q = b avec i1(b) = 0 soit 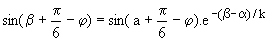 ; la valeur de b dépend de a et de j. ; la valeur de b dépend de a et de j.
On reste en mode 3 si Th1 et Th2' se bloquent avant l'amorçage de Th3' en a+p/6. On doit donc avoir
b < a+p/6. Pour une valeur donnée de j, il existe une valeur minimale de a qui permet de rester en mode 3. Le graphe de la fig.8 donne la valeur aL de l'angle d'amorçage séparant les fonctionnement en mode 3 et 1 suivant la valeur de j.
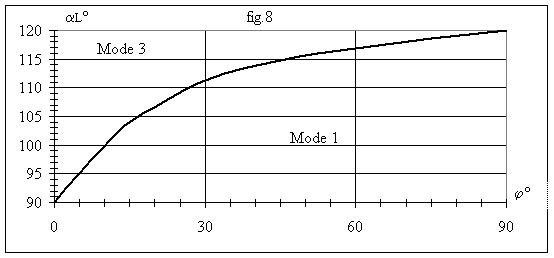
De b à a+60°, tous les thyristors sont bloqués donc toutes les grandeurs sont nulles.
L'analyse se complète sur la période suivant la même méthode que sur charge R :
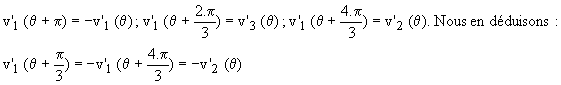
La fig.9 donne l'allure des grandeurs pour a = 120° et j = 60°
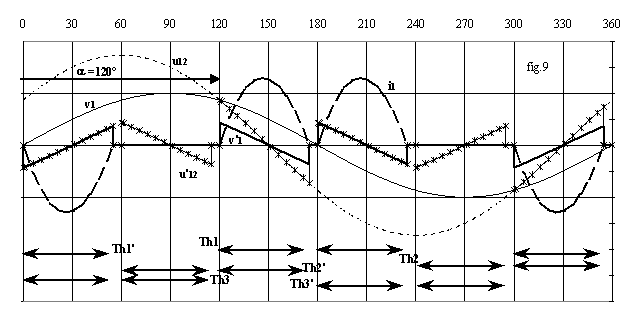
Ø Mode 1 = 2 ou 3 thyristors passants : à q = a, on amorce Th1 alors que Th2' et Th3 conduisent; on a donc v'1 = v1, v'2 = v2 et v'3 = v3. En posant X=L.w, il vient R.i1+X.di1/dq = v1= Vmax.sinq ;
R.i2+X.di2/dq = v2 = Vmax.sin(q-2p/3) ; R.i3+X.di3/dq= v3 = Vmax.sin(q+2p/3) . En résolvant les équations avec les conditions initiales i1(a)=0 ; i2(a) = -i3(a) = Io, nous obtenons :
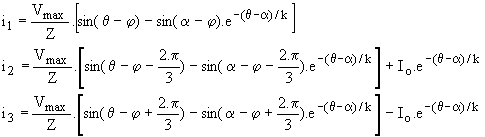
Ce régime prend fin avec le blocage de Th3 pour i3 (b) = 0; nous en tirons une relation entre b et Io : 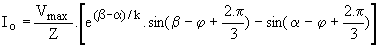 . .
Pour q > b , Th1 et Th2' conduisent seuls et v'1 = -v'2 = u2 / 2 et i2 = - i2. La résolution de R.i1+X.di1/dq = u12 /2= (Ö3.Vmax/2).sin(q+p/6) donne
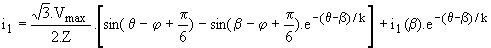
en remplaçant i1(b) par la valeur atteinte par ce courant juste avant le blocage de Th3, il vient
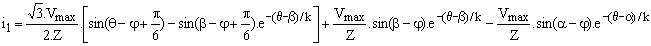
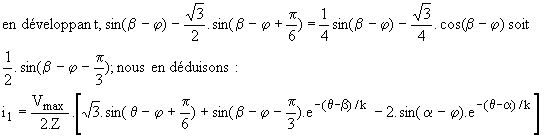
Pour calculer b, nous utilisons les symétries des courants : i1(a+p/3) = -i2(a) = - Io.
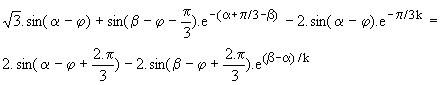
Nous complétons ensuite l'étude pour le reste de la période en utilisant les symétries des courants.
La fig.10 donne l'allure des grandeurs pour a = 60° ; j = 30°.
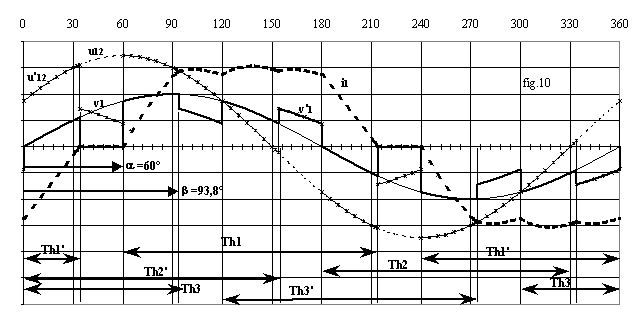
2.4 Calcul de la tension efficace
Soit V' la tension efficace aux bornes d'une phase de la charge; nous avons :
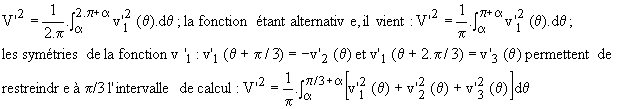
Nous devons envisager divers cas suivant le type de charge et le mode de fonctionnement.
Charge R - L
Dans ce cas, nous devons envisager les modes 1 et 3.
Ø Mode 1 : si a < aL, nous fonctionnons en mode 1; Th1, Th2' et Th3 conduisent de a à b imposant
v'1 = v1, v'2 = v2 et v'3 = v3.
Th1 et Th2' conduisent de b à a+p/3, imposant v'1 = -v'2 = u12/2 , v'3 = 0. Nous en déduisons :
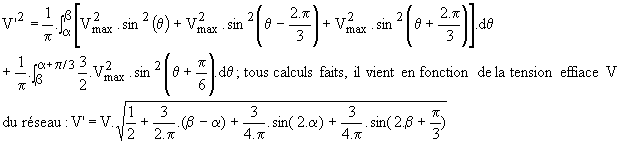
Ø Mode 3 : si a > al, nous fonctionnons en mode 3; Th1 et Th2' conduisent de a à b imposant
v'1 = -v'2 = u12/2, v'3 =0; de b à a+p/3, tous les thyristors sont bloqués et les tensions sont nulles . Nous en déduisons :
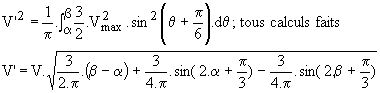
Charge R
Ø Mode 1 : le gradateur fonctionne dans ce mode si 0° < a < 60°. Le calcul est identique à celui fait pour la charge R-L en prenant b = 60°; il vient donc :
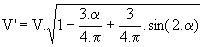
Ø Mode 2: le gradateur fonctionne dans ce mode si 60° < a < 90°. Th1 et Th2' conduisent de a à a+p/3. Le calcul de ce mode est celui fait pour la charge R-L en mode 3 avec b = a+p/3; il vient donc : 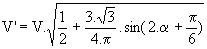
Ø Mode 3: le gradateur fonctionne dans ce mode si 90° < a < 150°. Th1 et Th2' conduisent de a à 5.p/6. Le calcul de ce mode est celui fait pour la charge R-L en mode 3 avec b = 5.p/6; il vient donc : 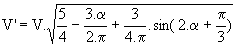
2.5 Harmoniques des grandeurs
Compte tenu des symétries de la tension v'1, sa décomposition en série de Fourier ne contient pas d'harmoniques de rang pair ni de rang multiple de 3. Les harmoniques sont donc de fréquence f, 5.f, 7.f, 11.f, 13.f, 17.f….
L'harmonique de rang n de v'n est de la forme :
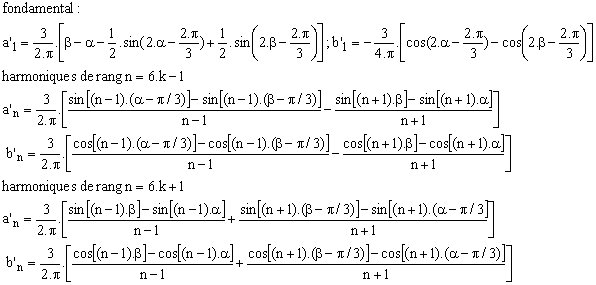
Pour une charge R, on peut reprendre les formules ci-dessus avec :
Ø Mode 1 : le gradateur fonctionne dans ce mode si 0° < a < 60°. Le calcul est identique à celui fait pour la charge R-L en prenant b = 60°.
Ø Mode 2: le gradateur fonctionne dans ce mode si 60° < a < 90°. Th1 et Th2' conduisent de a à a+p/3. Le calcul de ce mode est celui fait pour la charge R-L en mode 3 avec b = a+p/3.
Ø Mode 3: le gradateur fonctionne dans ce mode si 90° < a < 150°. Th1 et Th2' conduisent de a à 5.p/6. Le calcul de ce mode est celui fait pour la charge R-L en mode 3 avec b = 5.p/6.
Pour calculer les harmoniques du courant i1, il suffit de faire une étude en régime sinusoïdal à chaque fréquence:
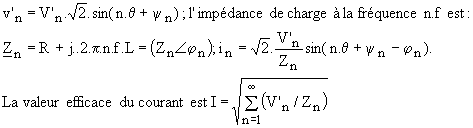
2.6 Étude énergétique
Le réseau étant purement sinusoïdal, seul le fondamental de l'intensité peut créer de la puissance active et de la puissance réactive. Ce fondamental est :

2.7 Exemple
Un réseau équilibré 230/400 V de fréquence f = 50 Hz alimente à travers le gradateur une charge R - L avec R = 12 W et L = 60 mH.
Nous avons 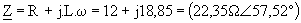 . .
D'après la fig.8, le mode 1 existe pour 57,52° < a < 117°.
Ø Prenons d'abord a = 75° : Th1, Th2' et Th3 conduisent de a à b =117,3° puis Th1 et Th2' conduisent de b à a +60°. Les formules établies en mode 1 donnent V' = 200 V et les valeurs des harmoniques du tableau ci-dessous :
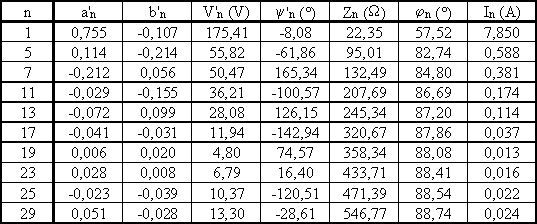
Nous en déduisons la valeur efficace du courant I = 7,88 A, les puissances active P = 2 238 W, réactive
Q = 4 933 VAR, efficace S = 5 440 VA, déformante D = 505 VA et le facteur de puissance Fp = 0,411.
Ø Prenons a = 120° : Th1, Th2' conduisent de a à b =174,5° puis tous les thyristors sont bloqués de b à a +60°. Les formules établies en mode 3 donnent V' = 67,6 V et les valeurs des harmoniques du tableau ci-dessous :
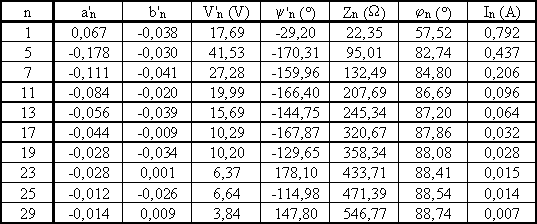
Nous en déduisons la valeur efficace du courant I = 0,88 A, les puissances active P = 31 W, réactive
Q = 545 VAR, efficace S = 604 VA, déformante D = 258 VA et le facteur de puissance Fp = 0,052.
3 étude de la structure s2
Un récepteur équilibré formé de trois impédances Z couplées en étoile est, vu de réseau, équivalent à un récepteur formé de trois impédances 3.Z couplées en triangle.
Le fonctionnement de la structure S2 est donc semblable à celui de la structure S1. Les formes d'onde des grandeurs i1 et u'12 dans la structure S2 sont identiques à celles de la structure S1; en revanche les formes d'onde de j1 et v'1 sont différentes dans les deux cas.
Faisons l'analyse pour une charge purement résistante :
u'12 = u12 = v'1 = R.j1; u'23 = u'31 = v'2 = v'3 = R.j2= R.j3 = -u12 /2; i1 = j1-j3 = 3.u12/2.R ; i2 = -i1 et i3 = 0.
Ø Mode 2 = 2 thyristors passants : ce mode existe pour 60° < a < 90°. enq = a, on amorce Th1 qui conduit avec Th2'; on a alors u'12 = u12 = v'1 = R.j1;
u'23 = u'31 = v'2 = v'3 = R.j2= R.j3 = -u12 /2; i1 = j1-j3 = 3.u12/2.R ; i2 = -i1 et i3 = 0.
Ø Mode 3 = 2 ou 0 thyristors passants : ce mode existe pour 90° < a < 150°. enq = a, on amorce Th1 qui conduit avec Th2'; on a alors u'12 = u12 = v'1 = R.j1;
u'23 = u'31 = v'2 = v'3 = R.j2= R.j3 = -u12 /2; i1 = j1-j3 = 3.u12/2.R ; i2 = -i1 et i3 = 0.
Cette combinaison impose u12> 0 soit q < 150°. A cet instant tous les thyristors sont bloqués et tous les courants sont nuls.
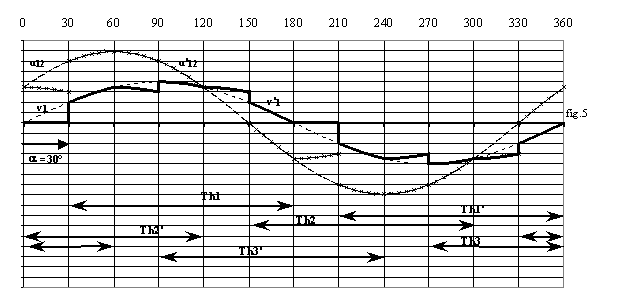
La fig.12 donne l'allure des grandeurs pour a = 30°.
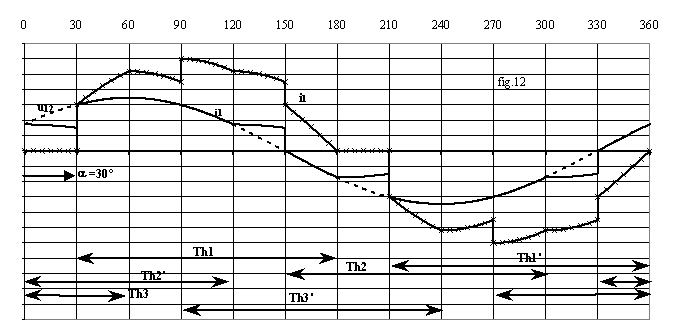
Les expressions des valeurs efficaces U' de u'12 et J de j1 sont celles de la structure S1 en remplaçant V par U, tension composée réseau; le courant en ligne a pour valeur efficace I = J.Ö3.
4 étude de la structure s3
4.1 Analyse
Le fonctionnement de cette structure diffère des précédentes car chaque phase peut fonctionner indépendamment des autres: si u12 > 0, on peut amorcer Th1 seul, un courant positif j1 circule dans la phase 1 et on a i1 = j1 = -i2 , i3 = 0.
Prenons la tension u12 comme origine des phases u12 = U.Ö2.sinq; Th1 est amorcé en q =a et Th1' en p+a., Th2 est amorcé en a+2.p/3 , Th3 en a+4.p/3.
Grandeurs par phase
Th1 étant passant, on a v'1 = u12 ; l'expression du courant pour une charge R - L est celle établie en monophasé: R.j1+X.dj1/dq = u12 = Umax.sin q. La solution est la somme de la solution générale de l'équation sans second membre R.i+X.di/dq = 0 soit
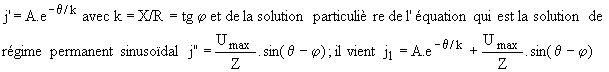
La constante A se calcule en écrivant que j1(a) = 0 soit
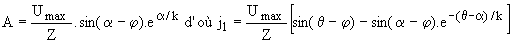 . .
Le thyristor Th1' ne peut être amorcé tant que Th1 conduit car la tension à ses bornes est alors légèrement négative. Th1 ne peut donc se bloquer que naturellement par annulation de j1.
j1 s'annule en b avec 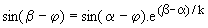 . .
On doit distinguer deux cas :
Ø a > j : dans ce cas, sin (a-j) est positif donc 0 < b-j < p; on en déduit b < j+p donc b < p+a. Th1 se bloque donc naturellement avant l'amorçage de Th1'. Th1' conduit de a+p à b+p; la tension u étant alternative, le courant j1 l'est aussi .
Ø a < j : dans ce cas, sin (a-j) est négatif donc b-j > p; on en déduit b > p+a. Th1 conduit donc encore lorsque Th1' reçoit l'impulsion d'amorçage. Le fonctionnement dépend du mode de commande; si les thyristors sont commandés par un peigne d'impulsions sur une durée p-a, lorsque Th1 se bloque, Th1' est toujours commandé donc conduit à partir de q = b. On a donc en permanence Th1 ou Th1' passant et v'1 = u12 en permanence; le courant j1 est sinusoïdal.
Courant en ligne
La loi des nœuds donne i1 = j1 - j3. Sa forme dépend de la valeur de a.
On amorce Th1 en a. Th2' amorcé en a - p/3 conduit jusqu'à b - p/3. Th1 et Th2' conduisent donc simultanément si a < b - p /3. Th3 amorcé en a -2. p /3 conduit jusqu'à b -2. p /3. Th1 et Th3 conduisent simultanément si a < b -2. p /3.
On retrouve les modes de fonctionnement pour un angle de commande a variant de j à p :
Ø Mode 1 = 3 ou 2 thyristors passants : si j < a < b -2. p /3, Th1, Th2' et Th3 conduisent simultanément de a à b -2. p /3;
on a alors 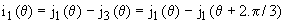 . .
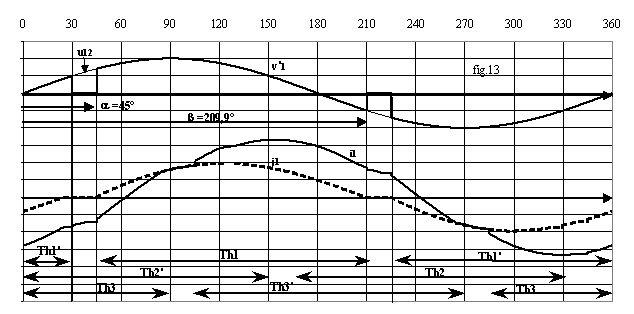
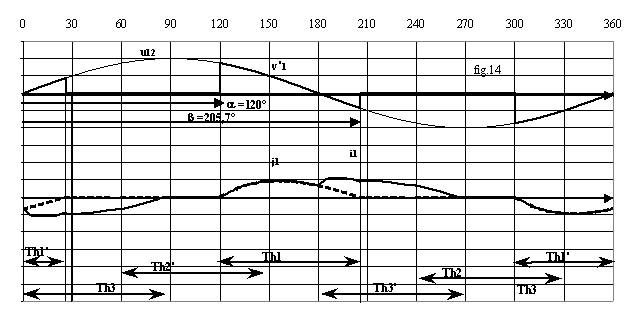
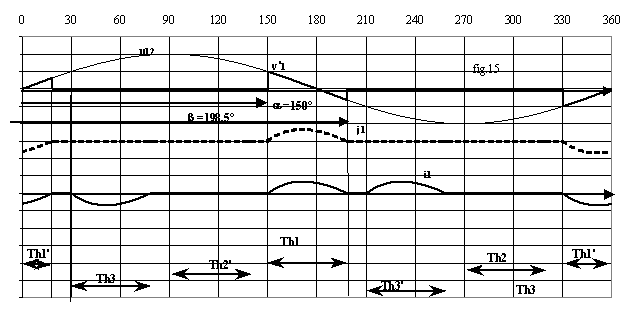
Pour j = 30°, les figures 13 à 15 donnent l'allure des grandeurs pour les trois modes
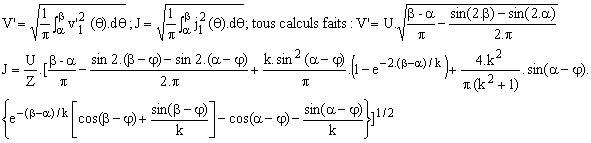
Le courant en ligne a pour valeur efficace I = J.Ö3.
Comme en monophasé, les tension et courants par phase contiennent tous les harmoniques de rang impair soit de fréquence f, 3.f, 5.f, 7.f, 9.f. Les harmoniques de rang 3.k+1 ( soit 1, 7, 13…) des trois phases forment un système équilibré direct donc I3k+1 = Ö3. J3k+1; les harmoniques de rang 3.k-1 ( soit 5, 11, 17…) des trois phases forment un système équilibré inverse donc I3k-1 = Ö3. J3k-1; les harmoniques de rang 3.k ( soit 3, 9, 15…) des trois phases forment un système homopolaire donc I3k-1 = 0 . Les courants en ligne ne contiennent donc pas d'harmoniques multiples de 3.
5 étude de la structure mixte
Dans la structure S1, nous remplaçons les thyristors Th1', Th2', Th3' par trois diodes D1',D2' et D3'.
5.1 Analyse sur charge R
Th1 est amorcé en a, Th2 en a+2.p/3 et Th3 en a+4.p/3. Il suffit d'étudier le fonctionnement entre a et a+2.p/3 puisque le système est triphasé donc i1(a+2.p/3) = i3(q) et i1(a+4.p/3)= i2(q).
Lorsque Th1 est amorcé, D1' est bloquée et on doit avoir au moins une diode passante parmi D2' et D3' pour que le courant puisse circuler. Les combinaisons possibles sont de redresseurs passants sont : Th1, D2', Th3 ou Th1, Th2, D3' ou Th1, D2',D3' ou Th1,D2' ou Th1,D3'.
Lorsque trois redresseurs sont passants v'1 = v1 = R.i1 , v'2 = v2 =R.i2 et v'3 = R.i3.
Th1, D2' et Th3 passants implique i1 > 0, i2 < 0 et i3 > 0, soit v1 > 0, v2 < 0 et v3 > 0, combinaison possible pour 0° < q < 60°.
Th1, Th2 et D3' passants implique i1 > 0, i2 > 0 et i3 < 0, soit v1 > 0, v2 > 0 et v3 < 0, combinaison possible pour 120° < q < 180°.
Th1, D2' et D3' passants implique i1 > 0, i2 < 0 et i3 < 0, soit v1 > 0, v2 < 0 et v3 < 0, combinaison possible pour 60° < q < 120°.
Lorsque Th1 et D2' conduisent, v'1 = -v'2 = u12 /2 = R.i1 = -R.i2; il faut u12 > 0. Mais il faut aussi que D3' soit polarisée en inverse. La tension anode- cathode de D3' est w3 = u23+u12/2 soit w3 = -3.v3/2. Il faut donc u12 > 0 et v3 >0 soit 0° < q < 60°.
Lorsque Th1 et D3' conduisent, v'1 = -v'3 = u13 /2 = R.i1 = -R.i3; il faut u13 > 0. Mais il faut aussi que D2' soit polarisée en inverse. La tension anode- cathode de D2' est w2 = u12+u13/2 soit w2 = -3.v2/2. Il faut donc u13 > 0 et v2 >0 soit 120° < q < 210°.
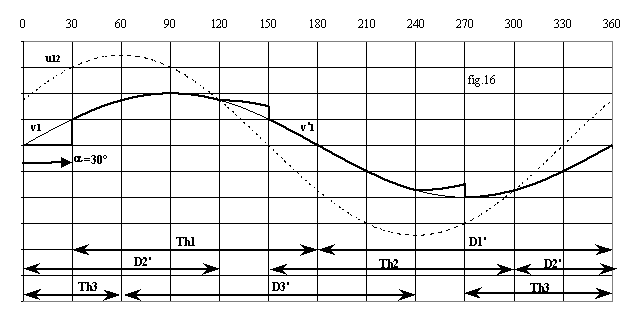
Ø Mode 1 = 3 ou 2 redresseurs passants : si 60° < a < 90° la combinaison Th1, D2', D3' passants est possible dès l'amorçage de Th1; D2' se bloque alors en 120° et Th1 et D3' conduisent jusque en 210°; Th2 est amorcé a + 120°, si a < 90°, a + 120° < 210°. Donc à partir de a + 120°, on retrouve trois redresseurs passants (D1', Th2, D3').
Si 0° < a < 60°, la combinaison Th1, D2', Th3 est possible; Th3 se bloque en 60° et on a Th1, D2', D3' passants jusque en 120°; en 120°, D2' se bloque et on a Th1 et D3' jusqu'à amorçage de Th2. On peut grouper ces deux cas puisque les tensions et le courants seront d'expression identique pour Th3 ou D'3 passants avec Th1 et D2'.
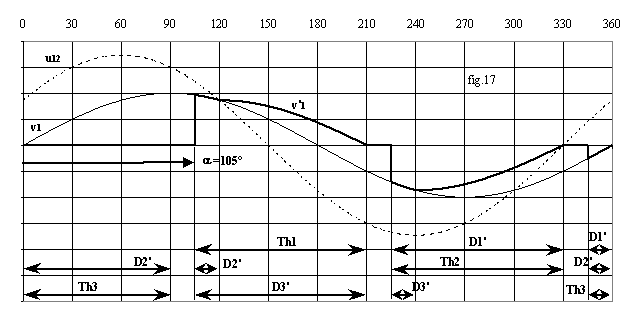
Ø Mode 2 = 3 , 2 ou 0 redresseurs passants : si a < 120° la combinaison Th1, D2' et D3' passants est possible dès l'amorçage de Th1; D2' se bloque alors en 120° et Th1 et D3' conduisent jusque en 210°; Th2 est amorcé a + 120°, si a > 90°, a + 120° > 210°. De 210° à a + 120°, tous les redresseurs sont bloqués.
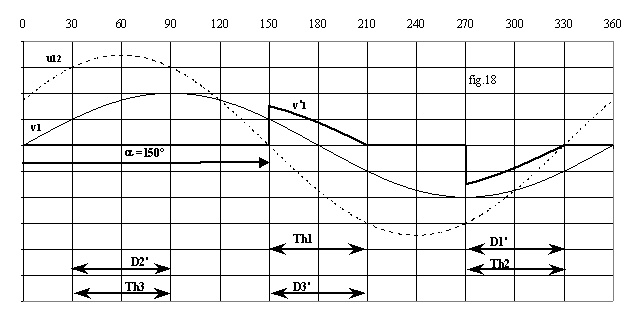
Ø Mode 3 = 2 ou 0 redresseurs passants : si 120° < a < 210°, la seule combinaison possible est Th1 et D'3 passants, car Th2 a été amorcé la dernière fois en a-240° et aucun redresseur ne peut conduire pendant plus de 120°.
On aura donc de 120 à 210° v'1 = -v'3 = u13 /2 = R.i1 = -R.i3; en 210°, u13 devient négative donc Th1 se bloque; comme Th2 n'est amorcé qu'en a + 120° > 240°, tous les redresseurs sont bloqués de 210° à a + 120°; si a > 210°, aucune combinaison n'est possible et Th1 ne s'amorce pas.
Les fig.16 à 18 donnent un exemple de forme d'onde dans chaque mode.
5.2 Analyse sur charge R - L
La charge est formée par une résistance R en série avec une inductance L. On pose 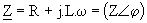 . .
L'inductance L interdit toute discontinuité du courant en ligne; chaque redresseur se bloque naturellement par annulation du courant qui le traverse; le courant i1 étant en retard sur la tension v'1, celle-ci est négative au moment du blocage de Th1.
Ø Mode 1 = 2 ou 3 redresseurs passants : à q = a > j, on amorce Th1 alors que D2' et Th3 conduisent; on a donc v'1 = v1, v'2 = v2 et v'3 = v3.
En posant X=L.w, il vient R.i1+X.di1/dq = v1= Vmax.sinq ; R.i2+X.di2/dq = v2 = Vmax.sin(q-2p/3) ; R.i3+X.di3/dq= v3 = Vmax.sin(q+2p/3) . E n résolvant les équations avec les conditions initiales
i1(a)=0 ; i2(a) = -i3(a) = Io, nous obtenons :
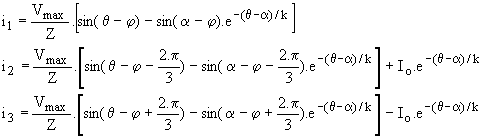
en q = b3, i3 s'annule puis devient négatif donc D3' prend le relais de Th3 et les équations des grandeurs ne sont pas modifiées.
Ce régime prend fin avec le blocage de D2' pour i2 (b2) = 0; nous en tirons une relation entre b2 et Io : 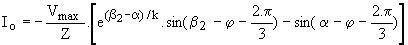 . .
Pour q > b2 , Th1 et D3' conduisent seuls et v'1 = -v'3 = u13 / 2 et i3 = - i1.
La résolution de R.i1+X.di1/dq = u13 /2= (Ö3.Vmax/2).sin(q -p/6) donne
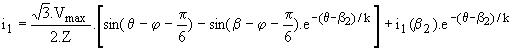
en remplaçant i1(b2) par la valeur atteinte par ce courant juste avant le blocage de D2', il vient
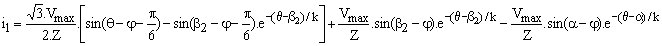 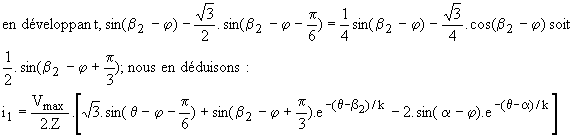
Pour calculer b2, nous utilisons les symétries des courants : i1(a+2.p/3) = i3(a) = - Io.
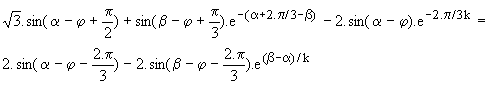
Tous calculs faits, nous obtenons : 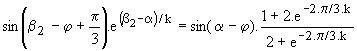
Nous complétons ensuite l'étude pour le reste de la période en utilisant les symétries des courants.
En q = b3 , Th3 se bloque; en écrivant que i3(b3) = 0 avec b3 < b2 , il vient :
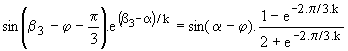
Th1 se bloque donc en b3 +2.p/3 et Th2 s'amorce en a +2.p/3; pour qu'il y ait toujours au moins un thyristor passant il faut que b3 +2.p/3 > a +2.p/3. La limite du fonctionnement en mode 1 est donc atteinte pour al = b3 avec 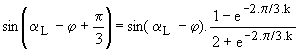
Ø Mode 2 = 0 , 2 ou 3 redresseurs passants : lors de l'amorçage de Th1 en q = a, tous les redresseurs sont bloqués en mode 2, donc tous les courants sont nuls. Pour q > a, Th1 et D2' et D3' conduisent donc
v'1 = v1, v'2 = v2 et v'3 = v3. Nous retrouvons les expressions du mode 1 avec Io = 0.
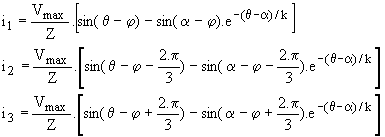
Ce régime prend fin avec le blocage de D2' en q = b2 : 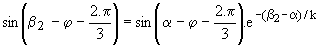 . .
Ensuite Th1 et D3' conduisent seuls v'1 = -v'3 = u13 / 2 et i3 = - i1. La résolution de R.i1+X.di1/dq = u13 /2= (Ö3.Vmax/2).sin(q -p/6) donne :
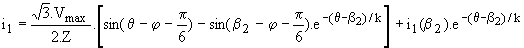
en remplaçant i1(b2) par la valeur atteinte par ce courant juste avant le blocage de D2', il vient
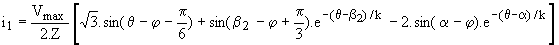
Les courants i1 et i3 s'annulent en q = b1 et tous les redresseurs sont bloqués de b1 à a+2.p/3.
Nous en déduisons :
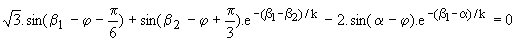
Lorsque on amorce Th1, tous les courants sont nuls en mode 2; pour que ce mode existe, c'est à dire pour que Th1, D2' et D3' conduisent, il faut :
v i1(a+) > 0; comme i1(a) = 0, on a donc un courant croissant soit di1(a+)/dq > 0; or
di1(a+)/dq = [ v1(a+)-R. i1(a+)]/X = v1(a+)/X; on doit donc avoir v1(a+) > 0.
v i2(a+) < 0; comme i2(a) = 0, on a donc un courant décroissant soit di2(a+)/dq < 0;
or di2(a+)/dq = [ v2(a+)-R. i2(a+)]/X = v2(a+)/X; on doit donc avoir v2(a+) < 0
v i3(a+) < 0; comme i3(a) = 0, on a donc un courant décroissant soit di3(a+)/dq > 0; or
di3(a+)/dq = [ v3(a+)-R. i3(a+)]/X = v3(a+)/X; on doit donc avoir v3(a+) < 0.
Cette combinaison des signes de tensions se produit uniquement de 60 à 120 °.
Le premier mode existe pour a < al ; or al varie de 90° pour j = 0 à 150° pour j = 90°.
si al > 120°, le mode 2 n'existera jamais, on passera directement du mode 1 au mode 3.
Pour que le mode 2 existe, il faut que j < 31,6°.
Ø Mode 3 = 0 ou 2 redresseurs passants : Th1 et D3' conduisent seuls de a à b1.
v'1 = -v'3 = u13 / 2 et i3 = - i1. La résolution de R.i1+X.di1/dq = u13 /2= (Ö3.Vmax/2).sin(q -p/6) donne avec i1(a) = 0:
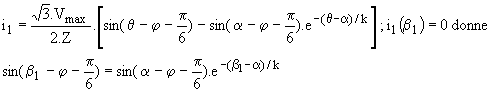
Le tableau ci-dessous donne les limites des modes en fonction du déphasage imposé par la charge :
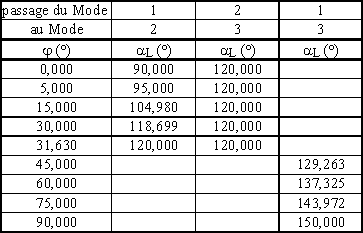
Le tableau ci-dessous donne les angles de blocage des redresseurs définis dans l'étude ci-dessus ainsi que les modes de fonctionnement..
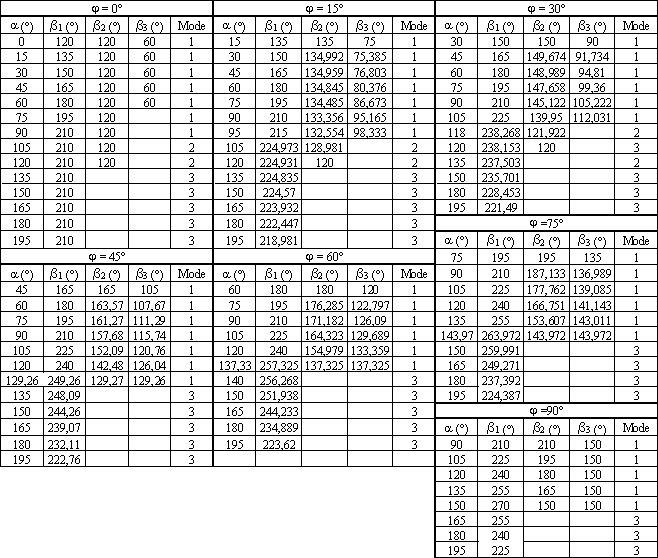
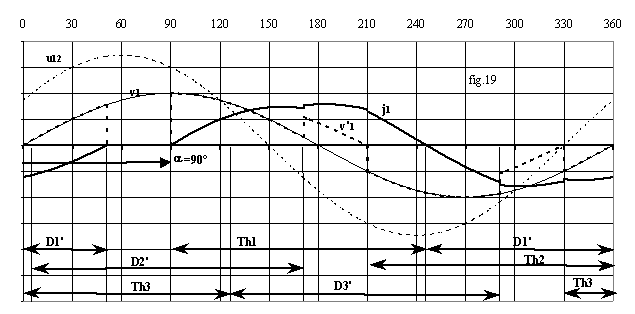
Les figures 19 et 20 donnent les formes d'onde en mode 1 et en mode 3 pour j = 60°.
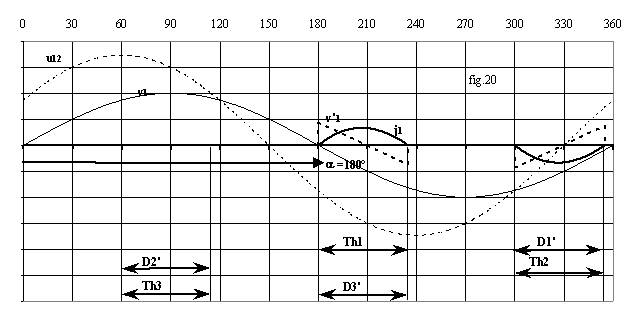
5.3 Calcul des valeurs efficaces
Compte tenu des symétries des grandeurs, nous avons :
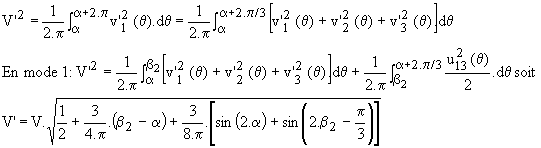
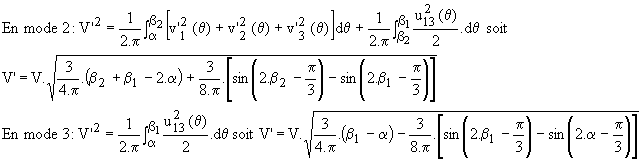
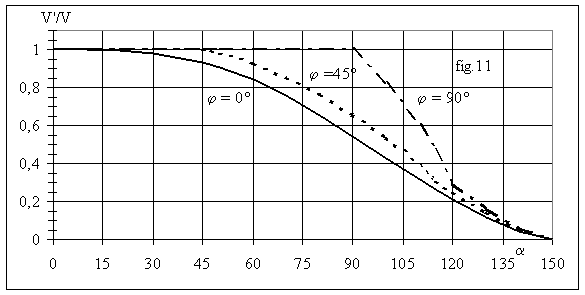
La fig.21 donne la variation de V'/V en fonction de a pour trois valeurs de j.
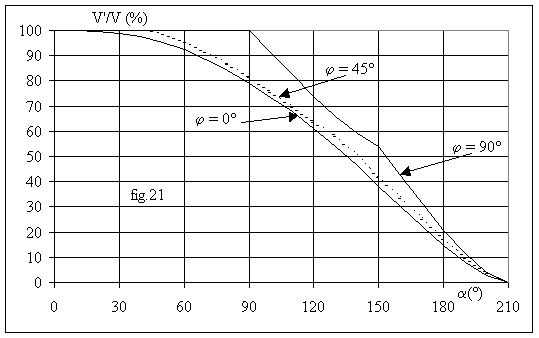
5.4 Analyse harmonique
En raison des symétries, les grandeurs ne comportent pas d'harmoniques de rang multiple de 3. Comme le montre la figure 19, les deux alternances de la tension v'1 ne sont pas symétriques, il y a donc des harmoniques pairs .
L'harmonique de rang n de v'n est de la forme :
Pour calculer les harmoniques du courant i1, il suffit de faire une étude en régime sinusoïdal à chaque fréquence:
Ø Mode 2 :
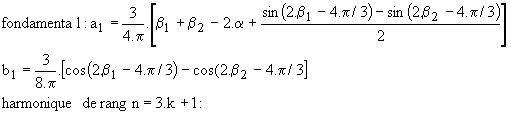
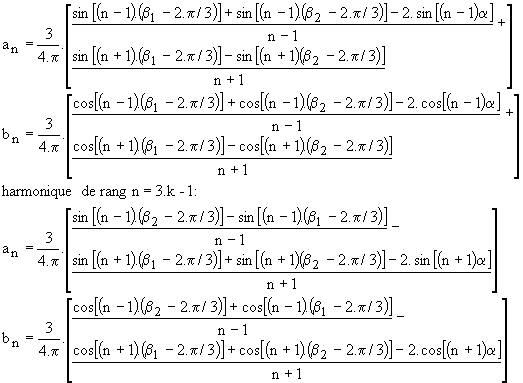
Ø Mode 3 :
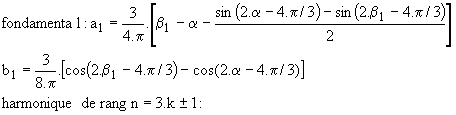
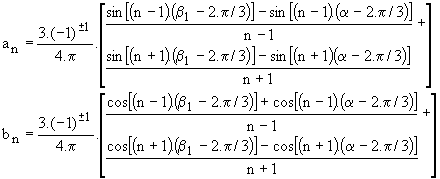
6 structure économique
Étudions la structure S4 (fig.4) pour une charge purement résistante. Th1 et Th2 sont commandés avec le même angle de retard a. Pour que les grandeurs de la charge ne comportent pas de composante continue, Th1' est commandé 180° après Th1 et Th2' 180° après Th2.

6.1 Combinaisons de conduction
La phase 3 étant toujours connectée au réseau et le couplage étoile imposant v'1+v'2+v'3 = 0, toutes les combinaisons avec 0, 1 ou 2 redresseurs passants sont possibles.
Ø
0 redresseur passant : v'1= v'2 = v'3 = 0
Ø 1 redresseur passant :
v si Th1 ou Th1' est passant la conduction se fait par les phases 1 et 3 :
v'1= - v'3 = u13 / 2 et v'2 = 0; si Th1 est passant i1 est positif donc v'1 l'est aussi; on doit donc avoir
u13 > 0 soit 30° < q < 210° ; si Th1' est passant i1 est négatif donc v'1 l'est aussi; on doit donc avoir
u13 < 0 soit 0° < q < 30° ou 210° < q < 360°.
v si Th2 ou Th2' est passant la conduction se fait par les phases 2 et 3 : v'2= - v'3 = u12 / 2 et v'1 = 0; si Th2 est passant i2 est positif donc v'2 l'est aussi; on doit donc avoir u12 > 0 soit 90° < q < 270° ; si Th2' est passant i2 est négatif donc v'2 l'est aussi; on doit donc avoir u12 < 0 soit 0° < q < 90° ou
270° < q < 360°.
Ø 2 redresseurs passants : on a alors conduction des trois phases avec v'1= v1 , v'2 = v2 et v'3 = v3.
v si Th1 et Th2' conduisent v1 > 0 et v2 < 0 soit 0° < q < 120°
v si Th1' et Th2 conduisent v1 < 0 et v2 > 0 soit 180° < q < 300°
v si Th1 et Th2 conduisent v1 > 0 et v2 > 0 soit 120° < q < 180°
v si Th1' et Th2' conduisent v1 < 0 et v2 < 0 soit 300° < q < 360°
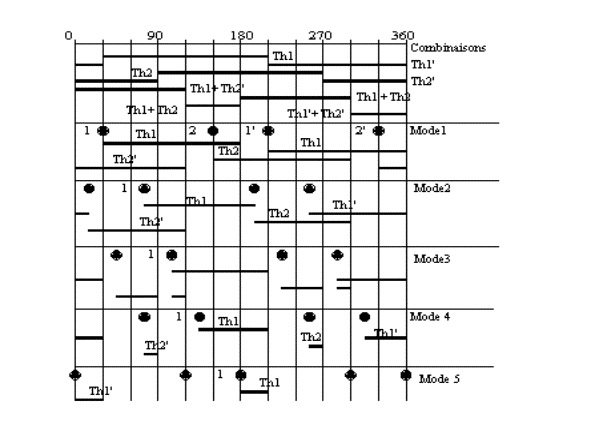
Les résultats sont repris dans le diagramme ci-dessous.
6.2 Analyse du fonctionnement
Pour déterminer les intervalles de conduction des 4 redresseurs, on marque sur l'échelle des temps les instants d'amorçage et on regarde à partir de chaque amorçage quelle est la combinaison possible. On a cinq modes de fonctionnement suivant la valeur de l'angle de commande a.
v Mode 1 : si 0° < a < 60°, lorsqu'on amorce Th1, Th2' est toujours passant et se bloque en 120° donc avant l'amorçage de Th2. Th1 continue à conduire seul; lors de l'amorçage de Th2, Th1 continue à conduire jusqu'à 180 et Th2 conduit seul jusqu'à l'amorçage de Th1' en p+a.
Comme les grandeurs sont alternatives vi(p+q)= - vi(q).
v Mode 2 : si 60° < a < 90°, lorsqu'on amorce Th1, Th2' est toujours passant et se bloque en 120° donc avant l'amorçage de Th2. Th1 continue à conduire seul; lors de l'amorçage de Th2, Th1 se bloque car la combinaison Th1,Th2' n'est plus possible pour q > 120° et Th2 conduit seul jusqu'à l'amorçage de Th1' en p+a.
v Mode 3 : si 90° < a < 120°, lorsqu'on amorce Th1, Th2' est toujours passant et se bloque en 120°. Th1 continue à conduire seul jusque en 210°; de 210° à 120+a aucun thyristor ne conduit. En 120+a Th2 s'amorce et conduit seul jusque en 270° ; il se bloque donc avant l'amorçage de Th1'. En 180+a Th1' s'amorce et conduit avec Th2 jusque en 300°, à condition que les impulsions de commande de Th2 durent au moins 60°. De 300 à 390°, Th1' conduit seul.
v Mode 4 : si 120° < a < 150°, lorsqu'on amorce Th1, Th2' est bloqué. Th1 conduit seul jusque en 210°; de 210° à 120+a aucun thyristor ne conduit. En 120+a Th2 s'amorce et conduit seul jusque en 270° ; il se bloque donc avant l'amorçage de Th1'.
v Mode 5 : si 150° < a < 210°, lorsqu'on amorce Th1, Th2' est bloqué; Th1 conduit seul jusque en 210°. Th2 est amorcé en 120+a > 270°, les combinaisons Th2 seul ou Th2 avec Th1 sont impossibles et Th2 ne conduit pas. Tous les thyristors restent bloqués jusqu'à l'amorçage de Th1' qui conduit de 180+a à 390°. Comme Th2, Th2' ne peut conduire puisque lors de son amorçage, aucune combinaison avec Th2' n'est possible.
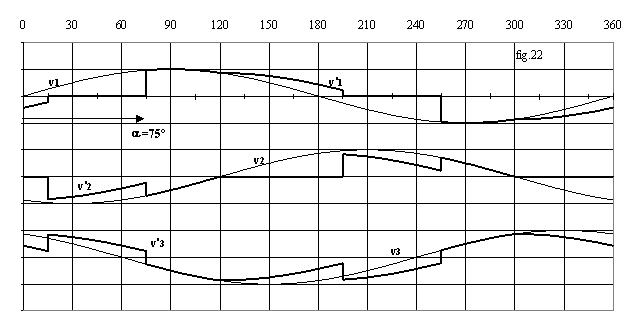
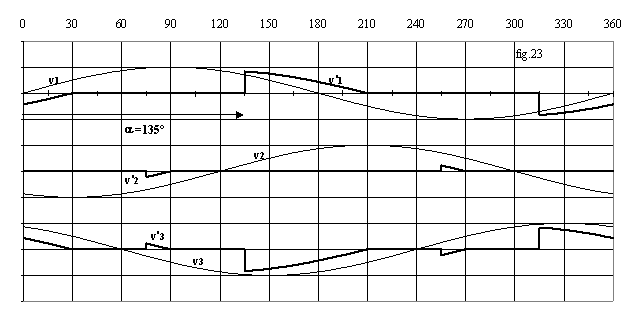
La fig.22 donne l'allure des tensions en mode 2 et la fig.23 en mode 4.
On constate que les grandeurs sont périodiques, alternatives mais non équilibrées.
6.3 Calcul des valeurs efficaces
Le calcul des valeurs efficaces des trois tensions v'1, v'2 et v'3 donne des formules complexes. La fig.24 donne l'évolution de ces grandeurs en fonction de l'angle de commande.
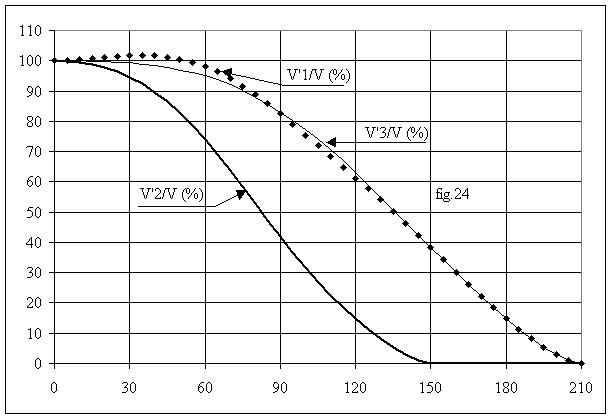
On constate le déséquilibre des grandeurs efficaces en particulier de la tension de la phase 2 toujours inférieure à celle des autres phases.
On peut réduire le déséquilibre en modifiant le retard à l'amorçage de Th2 et Th2'; il faut réduire cet angle d'environ 70% par rapport à celui de Th1 et Th1' pour avoir des tensions efficaces quasi équilibrées.
Les grandeurs n'étant pas équilibrées, la série de Fourier de v'1 contient tous les harmoniques de rang impair, y compris ceux de rang 3.k.
7 comparaison des structures
7.1 Contraintes sur les redresseurs
Comparons les quatre structures alimentées par le même réseau de tension composée efficace U et pouvant fournir une puissance maximale P sur une charge purement résistante:

Le montage S3 est celui qui nécessite des redresseurs de plus faible calibre en courant; de plus sa commande est simplifiée. Le montage S4 est plus économique car il ne demande que trois thyristors.
7.2 Critères de choix
Ø harmoniques injectés dans le réseau : la structure S3 est celle qui donne le moins de puissance déformante. La structure S1 peut aussi être utilisée bien que donnant de 1,5 à 2 fois plus de puissance déformante car la tension par redresseur est plus faible et donne des variantes simplifiant la commande, par exemple en branchant les redresseurs après la charge ce qui permet dans le cas de triacs d'avoir une référence de commande commune sur le neutre du gradateur. Le gradateur mixte est alors à proscrire.
Ø harmoniques dans la charge : lorsque le gradateur alimente un moteur, il est important de réduire les harmoniques du courant charge qui créent des couple parasites. Dans ce cas, on peut adopter la structure S1 ou S3, le choix se faisant suivant les valeurs de la tension et du courant (S1 si forte tension réseau, S3 si fort courant réseau).
Ø facilité de mise en œuvre : pour les montages de faible puissance alimentant des récepteurs passifs, la présence d'harmonique n'est plus un critère de choix. En général on utilise la structure S1 en utilisant toutes les variantes possibles ( thyristors après la charge, groupement en triangle des thyristors en aval de la charge …). en raison du déséquilibre des courants, la structure S4 est rarement utilisée
|








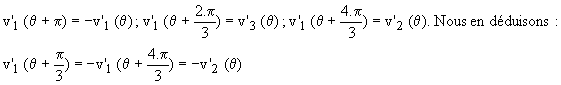

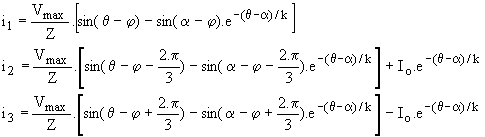
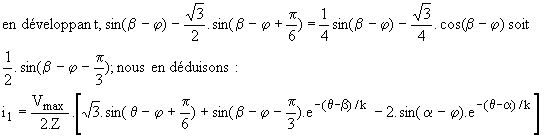
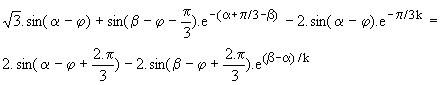

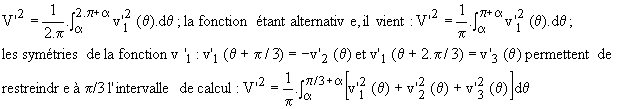
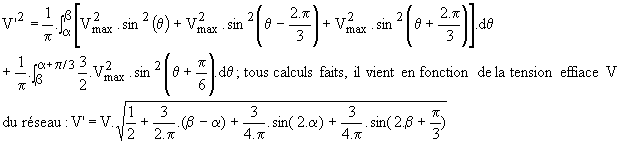
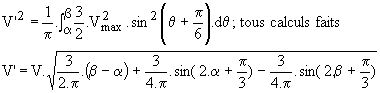
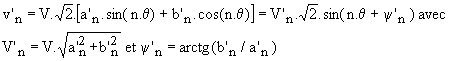
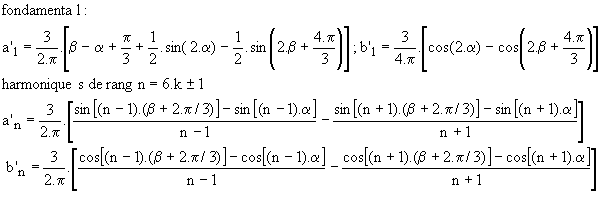
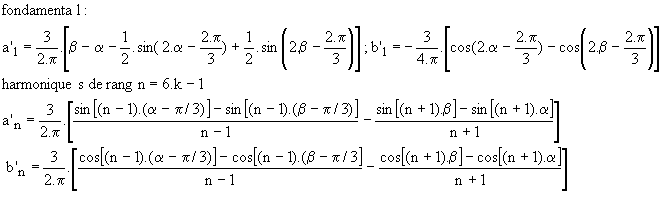
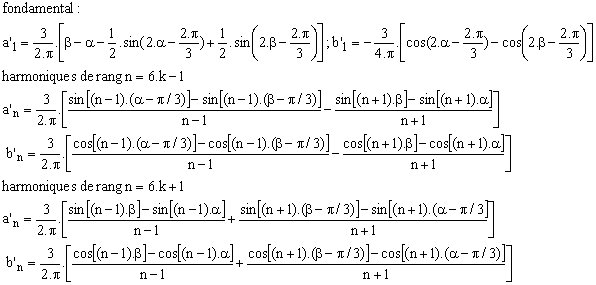
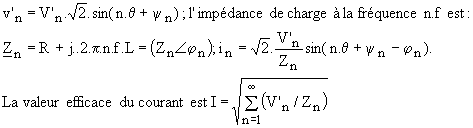




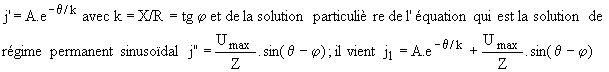

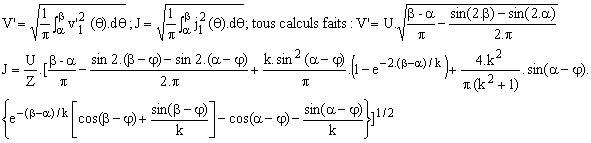



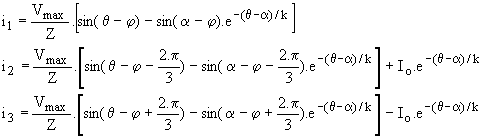
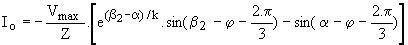 .
.