Calcul du courant i 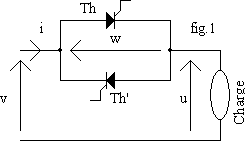
La charge est un dipôle R-L série d'impédance ![]() .
.
Supposons initialement les thyristors bloqués et i nul.
A q = a, on amorce Th; en posant X = L.w, il vient
R.i+X.di/dq = v = Vmax.sin q.
La solution générale de l'équation est :
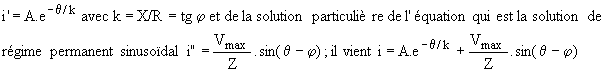
La constante A se calcule en écrivant que i(a) = 0 soit
![]() .
.
Le thyristor Th' ne peut être amorcé tant que Th conduit car w est alors légèrement négative. Th ne peut donc se bloquer que naturellement par annulation de i.
i s'annule en b avec ![]() .
.
On doit distinguer deux cas :
Ø a > j : dans ce cas, sin (a-j) est positif donc 0 < b-j < p; on en déduit b < j+p donc b < p+a.
Th se bloque donc naturellement avant l'amorçage de Th'. Th' conduit de a+p à b+p; la tension u étant alternative, le courant i l'est aussi donc on a i(q+p) = -i(q).
Ø a < j : dans ce cas, sin (a-j) est négatif donc b-j > p; on en déduit b > p+a. Th conduit donc encore lorsque Th' reçoit l'impulsion d'amorçage. Le fonctionnement dépend du mode de commande :
v si les thyristors sont commandés par de brèves impulsions de gâchette, l'impulsion envoyée sur Th' est inopérante puisqu'il est polarisé en inverse. Lorsque Th se bloque, Th' n'est plus commandé. Th' ne conduit donc jamais et le montage fonctionne en redresseur simple alternance.
v si les thyristors sont commandés par un peigne d'impulsions sur une durée p-a, lorsque Th se bloque, Th' est toujours commandé donc conduit à partir de q = b. On a donc en permanence Th ou Th' passant et u = v en permanence; le courant i est sinusoïdal.
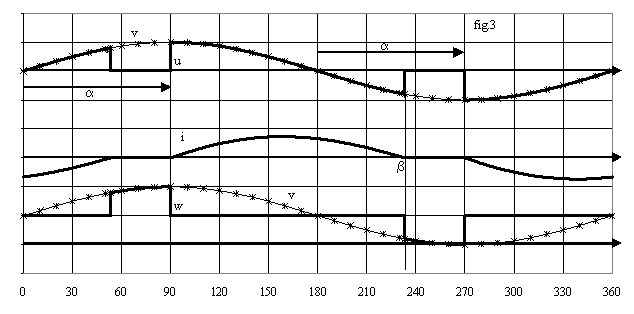
La fig.3 donne l'allure des grandeurs pour a = 90° et j = 60°.
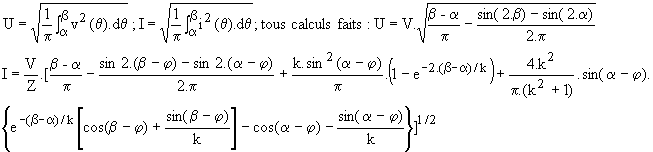
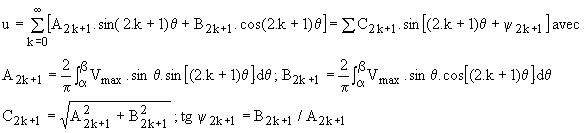
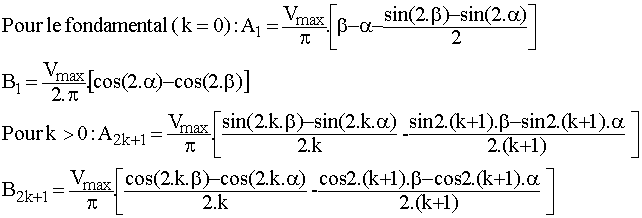
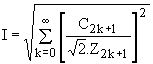 ;
;