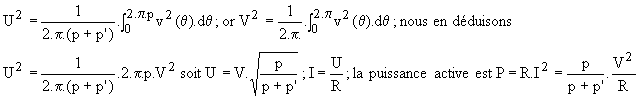Le gradateur monophasé est un convertisseur alternatif - alternatif, capable de faire varier la tension efficace aux bornes d'une charge monophasée.
Il est constitué par deux thyristors tête-bêche suivant la fig.1. Pour les faibles puissances, les deux thyristors sont remplacés par un triac.
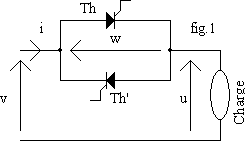
Les deux thyristors doivent être commandés avec le même angle de retard a pour obtenir une tension u alternative ( valeur moyenne nulle).
Deux modes de commande de l'énergie transférée à la source sont possibles :
Ø commande par la phase : la variation de la valeur efficace U est obtenue en agissant sur l'angle de retard a .
Ø commande par train d'ondes : les deux thyristors sont commandés plein onde pendant p périodes de la tension v puis sont bloqués pendant p' périodes. La variation de p/p' permet de commander la tension efficace U.
2 commande par la phase
2.1 Débit sur résistance
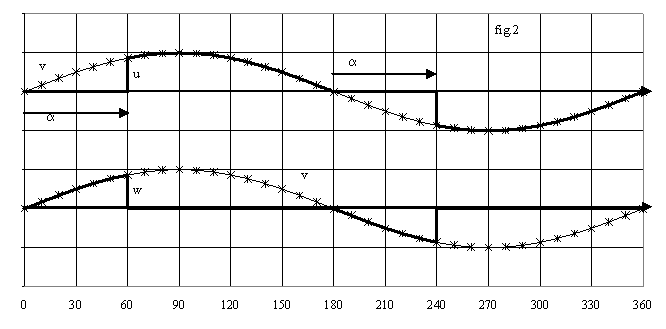
La charge est une résistance R imposant u = R.i. Lorsque v est positive, w est positive donc seul le thyristor Th est amorçable; il conduit à partir de a; on a alors u = v. Th se bloque naturellement en q = p où
v = u = 0 donc i = 0. Th' est amorçable quand v < 0; commandé avec le retard a, il s'amorce en p+a ; de p à p+a, Th et Th' sont bloqués donc i = 0 , u = 0 et w = v. Th' conduit de p+a jusqu'à l'annulation de i en en 2.p+a. La fig.2 donne l'allure de v, u et w.
2.2 Débit sur charge R-L
La charge est formée par une résistance R en série avec une inductance L. On pose  . .
Supposons initialement les thyristors bloqués et i nul.
A q = a, on amorce Th; en posant X = L.w, il vient R.i+X.di/dq = v = Vmax.sin q. La solution est la somme de la solution générale de l'équation sans second membre R.i+X.di/dq = 0 soit
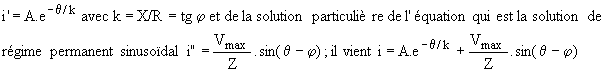
La constante A se calcule en écrivant que i(a) = 0 soit
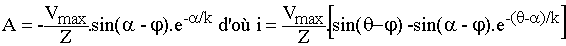 . .
Le thyristor Th' ne peut être amorcé tant que Th conduit car w est alors légèrement négative. Th ne peut donc se bloquer que naturellement par annulation de i.
i s'annule en b avec 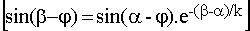 . .
On doit distinguer deux cas :
Ø a > j : dans ce cas, sin (a-j) est positif donc 0 < b-j < p; on en déduit b < j+p donc b < p+a.
Th se bloque donc naturellement avant l'amorçage de Th'. Th' conduit de a+p à b+p; la tension u étant alternative, le courant i l'est aussi donc on a i(q+p) = -i(q).
Ø a < j : dans ce cas, sin (a-j) est négatif donc b-j > p; on en déduit b > p+a. Th conduit donc encore lorsque Th' reçoit l'impulsion d'amorçage. Le fonctionnement dépend du mode de commande :
v si les thyristors sont commandés par de brèves impulsions de gâchette, l'impulsion envoyée sur Th' est inopérante puisqu'il est polarisé en inverse. Lorsque Th se bloque, Th' n'est plus commandé. Th' ne conduit donc jamais et le montage fonctionne en redresseur simple alternance.
v si les thyristors sont commandés par un peigne d'impulsions sur une durée p-a, lorsque Th se bloque, Th' est toujours commandé donc conduit à partir de q = b. On a donc en permanence Th ou Th' passant et u = v en permanence; le courant i est sinusoïdal.
En conséquence, il vaut mieux commander les thyristors par des peignes d'impulsions; dans ce cas, la tension efficace varie de 0 à V lorsque a varie de 0 à j et reste égale à V lorsque a < j .
La fig.3 donne l'allure des grandeurs pour a = 90° et j = 60°.
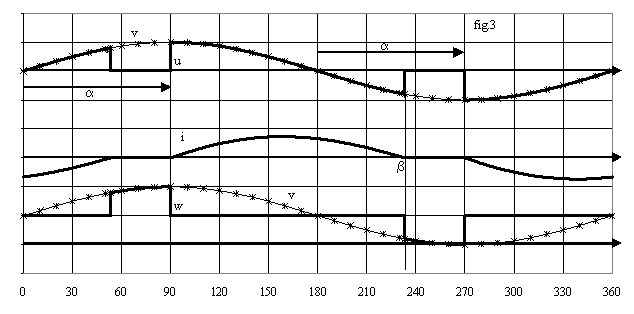
2.3 Étude de la charge
Nous nous plaçons dans le cas général d'une charge R-L.
Exprimons les grandeurs efficaces en fonction de la tension efficace du réseau V, de l'angle de commande et de l'impédance de charge.
Les grandeurs u et i sont alternatives et sont nulles de b à p+a; nous avons :
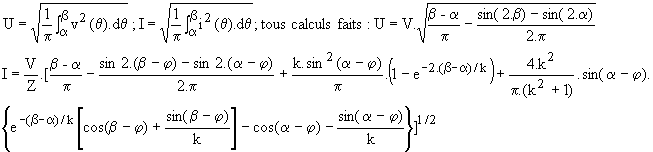
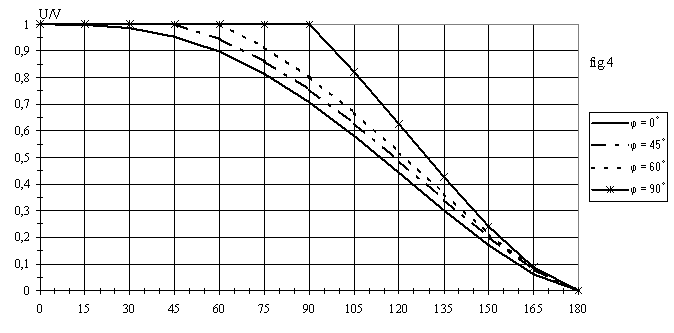
La fig.4 donne les variations de U/V en fonction de a pour diverses valeurs de j.
Étudions la décomposition en série de Fourier de la tension u. Cette tension étant alternative, elle ne contient que des harmoniques de rang impair:
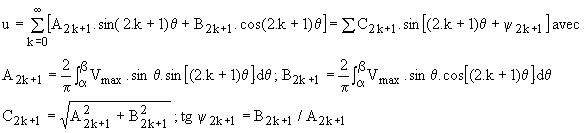
Tous calculs faits, on obtient :
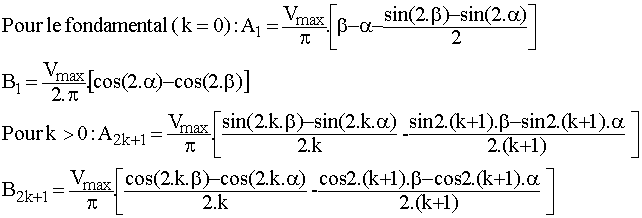
Les harmoniques du courant i s'en déduisent :
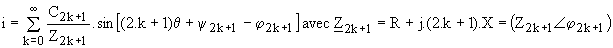
Dans le cas d'une charge purement résistive, il suffit de remplacer b par p.
2.4 Étude énergétique
Charge résistive
La puissance active consommée par la charge est P = U²/R . Le courant efficace est I= U/R . La puissance apparente fournie par le réseau est S = V.I = U.V/R.
Le facteur de puissance est Fp = P / S = U/V. Sa variation est donc représentée en fonction de a par la courbe de la fig.4 tracée pour j = 0.
Pour calculer les puissances réactive et apparente fournies par le réseau, il faut calculer le fondamental de i. Nous ferons le calcul ci-dessous dans le cas général.
Charge R - L
La tension v étant purement sinusoïdale, seul le fondamental de i peut créer les puissances active et réactive. Le fondamental du courant est
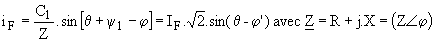 . .
Nous en déduisons :
P = V.IF.cosj' ; Q = V.IF.sin j' .
La valeur efficace de i peut être obtenue par la formule du paragraphe 2.3 ou à partir de la série de Fourier : 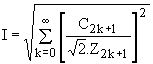 ; nous en déduisons la puissance apparente S = V.I et la puissance déformante ; nous en déduisons la puissance apparente S = V.I et la puissance déformante
D = Ö(S²-P²-Q²).
Exemple
Prenons V = 220 V et une charge R = 50 ohms. Le gradateur est commandé avec l'angle a = 45°.
Nous avons U = 0,953.V = 210 V ; I = U/ R = 4,2 A ; P = U.I = 880 W ; S = 923 VA; Fp = 0,953
A1 = 282,86 V ; B1 = -49,52 V; C1 = 287,16 V ; y1 = -9,93 °. IF = C1/R.Ö2 = 4,06 A;
j' = -y1 = 9,93 ° ; Q = Q = V.IF.sin j' = 154 VAR ; D = 232 VA.
Bien que la charge soit une résistance pure, nous constatons une consommation de puissance réactive due aux harmoniques.
Sous la même tension alimentons une charge formée d'une résistance R = 25 W en série avec une inductance L = 0,15 H. A 50 Hz, le déphasage introduit par la charge est j = 62 °. On a donc variation de U de 0 à V pour a variant de 180° à 62°. Prenons a = 90°.
La résolution numérique de l'équation 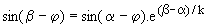 donne l'angle de blocage de Th' : donne l'angle de blocage de Th' :
b = 235° . Nous calculons les coefficients An et Bn de la série de Fourier de u; nous en déduisons la valeur efficace de chaque harmonique Un = Cn /Ö2 et la phase à l'origine yn de l'harmonique. Nous calculons ensuite l'impédance de la charge à la fréquence n.f. en module Zn et argument jn. Nous en déduisons l'intensité efficace In de chaque harmonique.
Le tableau ci-dessous donne les valeurs numériques.

Nous calculons l'intensité efficace 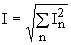 = 2,79 A. Le fondamental du courant a pour valeur efficace = 2,79 A. Le fondamental du courant a pour valeur efficace
IF = 2,74 A et le déphasage j' = (v, iF) = j1-y1 = 71,11°. Nous en déduisons P = V.IF.cosj' = 195 W ;
Q = V.IF.sin j' = 570 VAR ; S = V.I = 615 VA ; D = 120 VA.
Le facteur de puissance est Fp = P / S = 0,317.
Si on voulait obtenir la même puissance active en régime purement sinusoïdal, il faudrait avoir un courant sinusoïdal de même valeur efficace I = 2,79 A; la tension efficace serait U' = Z.I = 149 V et le déphasage
j = 62 °. Les puissances seraient P = U'.I.cos j = 195 W; Q = U'.I.sin j = 368 VAR ; S = U'.I = 416 VA et le facteur de puissance cos j = 0,469.
L'emploi du gradateur permet le réglage continu de U mais à puissance active constante, augmente de 35,5 % la consommation de puissance réactive et de 32,3 % celle de puissance apparente.
3 commande par trains d'onde
3.1 Étude des valeurs efficaces
Le gradateur est alimenté par un réseau de tension efficace V et de fréquence f. La charge est une résistance R.
Nous commandons pleine onde les thyristors durant p périodes et nous les bloquons pendant p' périodes. La période de la tension u est donc (p+p')/f. Calculons la tension efficace U :
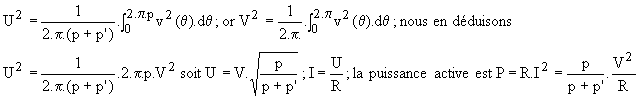
p et p' étant des nombres entiers, la tension et la puissance varient de façon discontinue.
La fig.5 donne l'allure des graphes pour p+p' = 10 = Cste.

Le réglage des grandeurs est d'autant plus fin que p+p' est grand. Mais quand p+p' augmente, la fréquence f/(p+p') de u diminue.
Lorsque la charge possède une grande inertie, par exemple pour le chauffage d'un four, on peut avoir une basse fréquence sans constater de fluctuations de la température. Lorsque l'inertie est plus faible, par exemple pour la commande de lampes ou de moteurs, on doit limiter p+p' à environ 10 pour ne pas constater des fluctuations de luminosité ou de vitesse.
Cherchons la décomposition en série de Fourier du courant i; i est égal à v/R de 0 à 2.p.p et à 0 de 2.p.p à 2.(p+p').p. La fréquence étant f / (p+p'), l'harmonique de rang n est de fréquence n.f/(p+p') si n < p+p', la fréquence de l'harmonique est inférieure à la fréquence du réseau; on dit que l'on a des sous-harmoniques.
Posons N = p+p' et Imax = Vmax / R. La décomposition en série de Fourier de i est de la forme :

La fig.6 donne le spectre du courant pour p = 4 et N = 10.

L'harmonique de rang N est de fréquence f égale à celle de v. Son expression est iF = (p/N).Imax.sin(q).
Il est donc en phase avec v et sa valeur efficace est IF = (p/N).(V/R).
La puissance active est P = V.IF = (p/N).V²/R.
La puissance réactive est nulle comme le déphasage (iF , v).
La valeur efficace du courant est I = Ö(p/N).(V/R).
La puissance apparente est donc S = V.I = Ö(p/N).(V²/R) et le facteur de puissance Fp = P/S = Ö(p/N).
La puissance déformante est D = Ö[(p/N).(1-p/N)]. V²/R.
Reprenons les valeurs de l'exemple du paragraphe 2.4.3 : V = 220 V et R = 50 ohms; pour avoir la même puissance P = 880 W qu'avec la commande à réglage de phase, il faut que p/N = 0,909. Si on prend N = 10, on aura p = 9,09 soit p = 9. On en déduit P = 871 W ; Q = 0; S = 918 VA ; Fp = 0,948 et D = 290 VA.
4 APPLICATIONS
4.1 Réglage de la tension efficace
Le gradateur permet de faire varier la tension efficace aux bornes d'une charge.
On l'utilise pour :
v le chauffage électrique : climatiseurs, fours …
v la commande d'éclairage : appareils à lampes halogènes, projecteur de spectacle …
v la commande de moteurs monophasés : moteurs universels ou asynchrones
En monophasé, la puissance fournie est limitée à quelques kilowatts; le plus souvent on utilise un triac comme interrupteur bidirectionnel.
Le plus souvent on utilise la commande par l'angle de phase; la commande par train d'ondes est réservé aux charges résistives ne nécessitant pas une grande précision de réglage de tension.
Ø avantages :
v simplicité de réalisation : un triac ou deux thyristors avec une électronique de commande simple.
v réglage progressif de la tension U de 0 à V quelle que soit la charge
v faible facteur de puissance surtout lorsque la tension U est proche de 0
v injection d'harmoniques dans le réseau
4.2 Interrupteur statique
Le gradateur fonctionne alors en tout ou rien avec U = V ou U = 0. Il peut remplacer un contacteur statique.
Ø On peut avoir de nombreuses opération Marche - Arrêt sans usure mécanique, sans bruit de fermeture ou d'ouverture.
Ø On peut aussi choisir l'instant de fermeture pour imposer la tension charge au moment de la fermeture; ceci permet d'éliminer les régimes transitoires.
Étudions par exemple la mise sous tension d'un transformateur; le réseau délivre une tension sinusoïdale
v = Vmax.sin (w.t) ; on alimente le transformateur à partir de l'instant to.
La tension impose le flux v = - dj /dt soit soit dj = -Vmax.sin(w.t); en intégrant, il vient
j = (Vmax/w).cos(w.t) +A = F.cos(w.t)+A; le flux est nul en to et ne peut être discontinu; on a donc
A = - F.cos(w.to) et j = F.[cos(w.t)- cos(w.to)]. La valeur maximale du flux est
Fmax = F(1+| cos(w.to)|). Le transformateur est calculé pour que le flux de régime permanent F place le circuit magnétique en légère saturation. Si to = 0, le flux atteint la valeur 2.F correspondant à une forte saturation donc à un très fort courant magnétisant. Ce courant d'appel s'amortit rapidement en raison des pertes magnétiques mais peut être suffisant pour faire déclencher les protections.
Si w.to = p/2, le flux maximal reste égal à F et le flux est sinusoïdal dès la mise sous tension.
Avec un interrupteur statique, on peut détecter l'instant où v est maximale et mettre sous tension le transformateur à cet instant.
On utilise cette méthode lorsque les mises sous tension sont fréquentes par exemple dans les machines à souder par point.
4.3 Compensation de puissance réactive
En régime sinusoïdal, lorsqu'une charge fonctionne avec un mauvais facteur de puissance, on doit relever ce facteur de puissance en branchant des condensateurs en parallèle. Si la puissance réactive consommée est variable, on doit adapter la valeur de la capacité à la charge. Plusieurs moyens peuvent être utilisés :
Ø mettre en service les condensateurs suivant la demande à l'aide de gradateurs fonctionnant en tout ou rien; cette méthode permet un réglage rapide de la puissance réactive mais pose des problèmes d'enclenchement; en effet, on ne peut appliquer une discontinuité de tension à un condensateur; il faut donc comparer la tension du condensateur à celle du réseau et fermer le gradateur lorsque les deux tensions sont égales.
Ø mettre en service tous les condensateurs et ajuster la puissance réactive avec une inductance en série avec un gradateur à commande de phase; on peut ainsi régler de façon continue la puissance réactive (fig.7).

Le condensateur absorbe la puissance réactive Qc = -C.w.V² ; l'inductance absorbe une puissance réactive variant de 0 pour a = 180° à V²/L.w pour a = 90°. La puissance absorbée par le circuit de compensation varie continûment de -C.w.V² à -C.w.V² + V²/L.w.
Pour une charge purement inductive d'impédance X = L.w, l'équation de la charge durant la conduction du triac est L.di/dt = v(t) soit X.di/dq = Vmax.sin(q) ; on en déduit i = A - (Vmax / X).cos(q).
Avec i(a) = 0, il vient i = (Vmax / X).[cos(a) - cos(q)].
Le triac se bloque pour q = b avec cos(b) = cos(a) soit b = 2.p - a .
La tension aux bornes de l'inductance est U = V. Ö{[2*p -2*a +sin(2*a)]/p}
La puissance réactive de l'inductance est Q = U² / X
Faisons un exemple numérique. Une charge alimentée sous V = 220 V a un facteur de puissance constant cos jch =0,6 AR et absorbe une puissance active P variant de 1 à 5 kW. On veut pouvoir régler à 1 le facteur de puissance pour toute valeur de P.
La puissance réactive de la charge varie de 1,33 kVAR à 6,67 kV; le compensateur doit donc pouvoir absorber de -1,33 kVAR à -6,67 kVAR.
Pour Qcomp = -6,67 kVAR, le gradateur est commandé avec a = 180° donc iL = 0 et la branche ne consomme pas de puissance réactive. Le condensateur absorbe donc QC = -C.w.V² soit QC = -6 670 VAR donc C = 439 µF à f = 50 Hz.
Prenons C = 470 µF soit QC = -7150 VAR.
Pour Q = 1 330 VAR, le compensateur absorbe Qcomp = - 1330 VAR = QC+QL ; on doit donc avoir QL = 5 820 VAR; si le triac est alors commandé avec a = 90°, le courant il est sinusoïdal et QL = V²/L.w; nous en déduisons la valeur de l'inductance L = 26,5 mH. Prenons L = 25 mH.
On peut tracer le graphe de QL en fonction de l'angle de commande a. Pour une charge purement inductive, b = 2.p-a ; le calcul du fondamental vF de la tension donne B1 = 0; vF est donc en phase avec v de valeur efficace 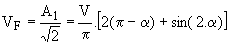 ; le fondamental if du courant est en quadrature arrière sur vF donc sur v, de valeur efficace VF/L.w = VF/X. ; le fondamental if du courant est en quadrature arrière sur vF donc sur v, de valeur efficace VF/L.w = VF/X.
La puissance active consommée par la branche gradateur est nulle et la puissance réactive est
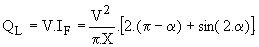
La figure 8 donne l'évolution de QL en fonction de a.

Le tableau ci-dessous donne les valeurs de a en fonction de la puissance P consommée par la charge.
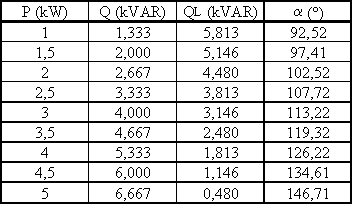
|


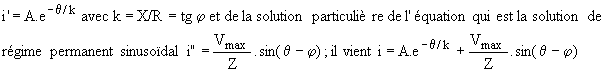

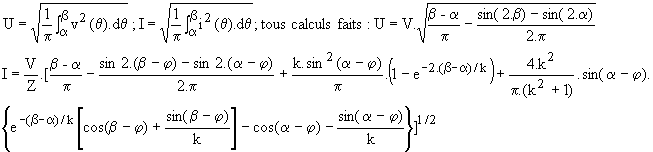

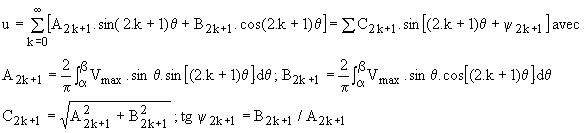
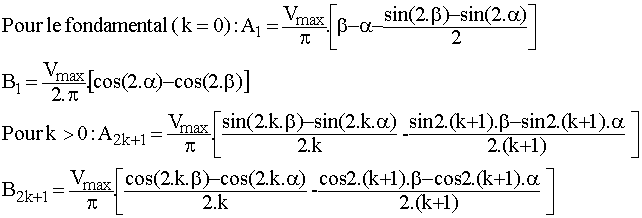
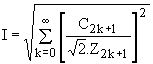 ; nous en déduisons la puissance apparente S = V.I et la puissance déformante
; nous en déduisons la puissance apparente S = V.I et la puissance déformante