Exercice 1 : Alimentation d'un four
Le schéma de l'alimentation est donné ci-dessous : 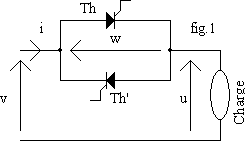
v tension efficace du réseau V = 230 V
v fréquence du réseau f = 50 Hz
v puissance maximale du four 1 800 W
Les deux thyristors sont amorcés avec le même angle de retard a variant de 0 à 180° .
|
Commande par la phase |
1.1 |
Calculer la résistance R du four |
P = V² / R donc R = 29,4 W
Cliquez ici |
1.2 |
On règle l'angle de retard a = 60°. Calculer la puissance dissipée par R |
U = V. Ö[(p - a +sin(2.a)/2)/p] = 206 V
P = 1 448 W
Cliquez ici |
1.3 |
Pour le point de fonctionnement ci-dessus, calculer la valeur efficace du fondamental du courant j et le déplacement du facteur de puissance |
Fondamental de la tension u :
A1 = (Vmax/p).( p - a +sin(2.a)/2) = 261,7 V
B1 = (Vmax/2.p).(cos(2.a) - 1) = - 77,7 V
C1 = 273 V donc U1eff =C1/Ö2 = 193 V ; J1 = U1/R = 6,57 A
phase de u1 : y1 = atan(B1/A1) = -16,5 °
j1 est en phase avec u1 donc j1 = 16,5 ° ; DPF = cosj1 = 0,96
Cliquez ici |
1.4 |
Pour le point de fonctionnement ci-dessus, calculer les puissances réactive, apparente et déformante ainsi que le facteur de puissance |
La puissance réactive est créée par le fondamental Q = V.J1.sin j1 = 430 VAR
La puissance apparente prend en compte les harmoniques :
S = V.J = V.U/R = 1 612 VA
D = Ö(S² -P² -Q² ) = 563 VA ; facteur de puissance Fp = P / S = 0,898
Cliquez ici |
Commande par trains d'onde
On commande les thyristors pleine onde pendant p périodes et on les bloque pendant p' périodes.On impose N = p + p' = 15
|
1.5 |
Combien de valeurs différentes de la puissance peut-on obtenir ? |
P = U² / R et U = V. Ö(p/N) ; p peut prendre 16 valeurs de 0 à 15 donc on a 16 puissances différentes
Cliquez ici |
1.6 |
Quelle est la valeur de p qui donne la puissance la plus proche de 1 450 W ? |
U = Ö(P.R) = 206 V p = N.U² / V² = 12,1
p étant entier on prendra p = 12 donc U = 205,7 V et
P = 1 440 W
Cliquez ici |
1.7 |
Pour cette valeur, quelle est la fréquence de u ? |
Sa fréquence est f' = f / N = 3,33 Hz
Cliquez ici |
|
Pour cette valeur, calculer l'harmonique de j de fréquence égale à celle du réseau |
C'est l'harmonique de rang N : jF = (p/N).Imax.sin(q).
sa valeur efficace est J F = (p/N).(V/R) = 6,26 A et il est en phase avec v
On peut aussi dire que P = V. JF
Utiliser les formules du montage PD2 mixte du chapitre "Convertisseurs monophasés", paragraphe 3.4
Cliquez ici |
1.9 |
Pour cette valeur calculer les puissances réactive, apparente, déformante et le facteur de puissance |
(iF,v) = 0 donc Q = 0
Jeff = U/R = 7 A ; S = V.Jeff = 1 612 VA
D = 725 VA ; Fp = P /S = 0,89
Cliquez ici |
1.10 |
Comparer les deux modes de commande |
Pour la même puissance P, on a la même apparente; le facteur de puissance est donc le même. La commande par train d'ondes a l'avantage de ne pas consommer de puissance réactive mais a une puissance déformante plus grande donc plus d'harmoniques dans le courant en ligne
Cliquez ici |
Exercice 2 : Alimentation d'une charge inductive
La charge est formée par une résistance R = 50 W en série avec une inductance L = 0,1 H
Le réseau est de valeur eficace V = 400 V et de fréquence f = 50 Hz
La commande se fait par la phase avec le montage de l'exercice 1
|
2.10 |
Calculer le module et l'argument de l'impédance de charge à la fréquence f |
Z = R + j.L.w = 50 +j 31,4 = (59,1 W ; 32,1 °)
Cliquez ici |
2.11 |
Quelle est la plage de variation de l'angle de commande a qui permet de faire varier la tension efficace charge U de 0 à son maximum |
Pour a = j = 32,1 °, on a la tension maximale U = V et pour a = 180°, on a U = 0
Cliquez ici |
2.12 |
Pour a = 90°, donner l'expression de l'intensité j lors de la conduction de Th |
Avec X = L.w = 31,4 W ; k = X /R = 0628 ; Z = 59,1 W ; j = 32,1°, l'équation X.dj/dq + R.i = Vmax.sin q a pour solution
j = A.exp(-q/k) +(Vmax/Z).sin(q-j)
i(a) = 0 donne A = -(Vmax/Z).sin(a-j)exp(a/k) = -98,7 A
j = -98,7.exp(-q/k) +9,57.sin(q-j)
Cliquez ici |
2.13 |
Calculer la durée de conduction de Th |
Th se bloque en b pour j = 0 : 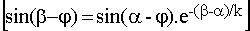
Cette équation doit être résolue numériqument par approximations successives ; on obtient b = 210,4 °
Th conduit donc sur un angle de 120,4 ° .
360 ° représente une période de 20 ms donc le temps de conduction est 6,69 ms.
Cliquez ici |
2.14 |
Représenter les graphes de v, u et j |
|
2.15 |
Calculer la valeur efficace de u |
U = V. Ö{(b - a) / p -[sin(2.b) - sin(2.a)]/(2.p)} = 291 V
Cliquez ici |
2.20 |
Calculer les harmoniques de u et i jusqu'au rang 9. En déduire la valeur de Jeff. |
u étant alternative, il n'y a que des harmoniques impairs :
un = An.sin(n.q) + Bn.sin(n.q) = Cn.sin(n.q + yn)
Zn = (Zn ; jn) avec Zn = Ö[R² +(L.n.w)²] et jn = atan (n.L.w /R)
in = C'n.sin(n.q + y'n) avec C'n = Cn / Zn et y'n = yn - jn

Jeff = Ö [ S (C'n²/2)] = 5 A
Cliquez ici |
2.21 |
Calculer les puissances active, réactive, apparente et déformante fournies par le réseau |
Les puissances active et réactive correspondent uniquement au fondamental de j : J1eff = C'1 / Ö2 = 4,81 A ; déphasage (j1 , v) = -y'1 = 51.64 °
P = V.J1eff.cos (j1 , v) = 1 193 W ; Q = V.J1eff.sin(j1 , v) = 1 508 VAR
S = V.Jeff = 2 000 VA ; D = Ö(S² - P² - Q²) = 550 VA
Cliquez ici |
Exercice 3 : Compensation de puissance réactive
On utilise le montage ci-dessous :

Le réseau est de valeur eficace V = 230 V et de fréquence f = 50 Hz
La commande du triac se fait par la phase.
|
3.1 |
Calculer la valeur de la capacité C pour que le condensatuer fournisse Qc = 3 kVAR
|
Qc = C.w.V² = 3 000 VAR donne C = 181 µF
Cliquez ici |
3.2 |
Calculer la valeur de l'inductance L pour que la bobine absorbe une puissance réactive maximale de 2 kVAR |
La puissance est maximale pour a = 0; on a alors VL = V et QL = V² / X avec X = L.w
On en déduit X = 26,45 W soit L = 84 mH
Cliquez ici |
3.3 |
On règle l'angle de commande a = 120 °. Calculer la puissance réactive absorbée par l'association L - C |
A l'alternance positive, le triac conduit de a à 2.p-a
U = V. Ö{[2*p -2*a +sin(2*a)]/p} = 144 V
QL = U² / X = 784 VAR
QL - QC = -2216 VAR pour l'association L - C
Cliquez ici |
3.4 |
La charge absorbe la puissance active P = 2 kW avec un facteur de puissance 0,7 AR. Calculer l'angle a pour que le réseau ait un facteur de puissance égal à 0,98 AR
|
Pour la charge P = 2 kW ; j = 45,6 ° ; Q = P.tgj = 2,04 kVAR
Pour le réseau P' = P , j' = 11,5 °, Q' = P'.tg j' = 406 VAR
Q' = Q + QL - Qc donne QL = 1 366 VAR
U = Ö(X.QL) = 190 V = V. Ö{[2*p -2*a +sin(2*a)]/p}
Cette équation se résoud numériquement et on obtient
a = 104,6 °
Cliquez ici |