Exercice 1 : Alimentation d'une locomotive
Le schéma de l'alimentation est donné ci-dessous : 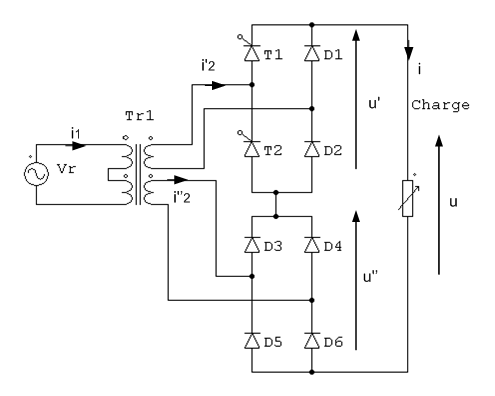
Le transformateur Tr1 a deux enroulements primaires de n1 spires branchés en série et deux enroulements secondaires identiques de n2 spires. Ce transformateur est supposé parfait.
v tension efficace du réseau Vr = 15 kV
v tension efficace par enroulement secondaire V2 = 500 V
La charge absorbe un courant constant d'ondulation négligeable I = 200 A.
Les deux thyristors sont amorcés avec le même angle de retard a variant de 0 à 180° .
|
1.1 |
Quelle est la valeur du rapport m = n2 / n1 ? |
Le primaire a 2.n1 spires et chaque secondaire a n2 spires donc
n2 / 2.n1 = V2 / Vr soit m = n2/n1 = 2. V2/Vr = 0,067
Cliquez ici |
1.2 |
Pour a = 90° représenter la tension d'un secondaire du transformateur, les tensions u', u" et u |
|
1.3 |
Quelle est la valeur moyenne U" du redresseur à diode ? |
Redresseur PD2 à diodes : U' =2.V2max / p = 450 V
Cliquez ici |
1.4 |
Quelle est, en fonction de a, l'expression de la valeur moyenne U' du redresseur mixte? |
Redresseur PD2 mixte : U' = (V2max /p).(1+cosa)
U' = 225. (1+cosa)
Cliquez ici |
1.5 |
Pour a variant de 180 à 0°, quelle est la plage de variation de la tension moyenne U? |
U = U' + U" = (V2max /p).(1+cosa) + 2.V2max /p
U" est constant et U' varie de 0 à 450 V donc U varie de 450 à 900 V
Cliquez ici |
1.6 |
Quelle relation a-t-on entre les intensités i'2, i"2 et i1 ? |
Equation aux ampères-tours :
2.n1.i1 - n2.i'2 - n2.i"2 = 0 soit
i1 = m.(i'2 + i"2)/2
Cliquez ici |
1.7 |
Pour a = 90°, représenter les intensités des courants i'2 , i"2 et i1 |
|
|
Pour a = 90°, calculer les puissances active, réactive, apparente et déformante fournies par chacun des deux ponts PD2 |
Aide |
P = Umoy . I , Q = Vmax.I.sin a / p , S = V.I.Ö(1-a/p) ; D = Ö(S² - P² - Q²)
Pour le pont mixte a = 90° :
P' = 45 kW ; Q' = 45 kVAR ; S = 70,7 kVA ; D = 30,8 kVA
Pour le pontde diodesa = 0° :
P' = 90 kW ; Q' = 0 kVAR ; S = 100 kVA ; D = 43.6 kVA
Utiliser les formules du montage PD2 mixte du chapitre "Convertisseurs monophasés", paragraphe 3.4
Cliquez ici |
1.9 |
Pour a = 90°, calculer la valeur efficace du courant i1 |
i1 = m.(i'2 + i"2)/2 = 0,033. (i'2 + i"2)
angle |
0 à 90 ° |
90 à 180° |
180 à 270° |
270 à 360° |
i'2 |
0 |
200 |
0 |
-200 |
i"2 |
200 |
200 |
-200 |
-200 |
i1 |
6,7 |
13,3 |
-6.7 |
-13.3 |
I1 = Ö[(6.7²*p+ 13.3²*p)/2.p] = 10,53 A
Cliquez ici |
1.10 |
Pour a = 90°, calculer les puissances active, réactive, apparente et déformante fournies par la source vr |
Les puissances active d'une part et réactive d'autre part s'ajoutent : P = P' + P" = 135 kW et Q = Q'+Q" = 70,7 kVAR
S = Vr.I1 = 158 kVA ; D = D = Ö(S² - P² - Q²) = 41,5 kVA
Cliquez ici |
1.11 |
La structure étudiée est-elle réversible ? |
Un redresseur n'est jamais réversible en courant; un redresseur à diodes ou mixte n'est pa réversible en tension; la structure n'est donc pas réversible.
Cliquez ici |
Exercice 2 : Alimentation réversible d'une machine à courant continu
On alimente une machine à courant continu par deux structures PD3 montées en antiparallèle suivant le schéma ci-dessous :
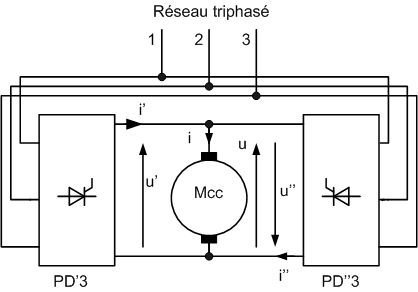
|
Etude de la machine continue
La machine fonctionne à flux constant. Son couple de pertes est supposé constant en valeur absolue.
On donne :
èla résistance de l'induit : Ri = 20 mW
èl'inductance de l'induit : Li = 400 µH
èla constante de flux : K = E / W = 10 V.s
|
2.10 |
La machine fonctionnant à vide à la vitesse n = 250 tr/min, on a mesuré le courant d'induit I = 10 A. Calculer la tesnion d'induit et le moment du couple de pertes. |
E = K.W = 261,8 V ; U = E + R.I = 262 V
Tem = Tu + Tr = Tr = K.I = 100 Nm
Cliquez ici |
2.11 |
On veut que la machine puisse fonctionner à une vitesse variant de -400 à +400 tr/min pour des courants d'induit variant de -200 à +200 A. Quelle est la plage de variation de la tension d'alimentation. |
E = K.W varie de -419 à +419 V
U = E + R.I varie donc de -423 à 423 V
Cliquez ici |
2.12 |
La machine fonctionne au point M1 défini par U = 250 V et Tu = 1 000 Nm. Quel est le quadrant de fonctionnement dans le plan n(Tu). Calculer la vitesse et le courant d'induit. |
U > 0 donc n > 0 , Tu > 0 donc quadrant 1 (Moteur sens +)
Tem = Tu + Tr = 1 100 Nm ; I = Tem / K = 110 A
E = U - R.I = 247,8 V ; W = E / K = 24,78 rd/s ;
n = 30.W/p = 237 tr/min
Cliquez ici |
2.13 |
La machine fonctionne au point M2 défini par U = 200 V et I = -180 A. Quel est le quadrant de fonctionnement dans le plan n(Tu). Calculer la vitesse et le moment du couple utile |
U > 0 donc n > 0 , I < 0 donc Tu < 0 donc quadrant 2 (Générateur sens +)
E = U - R.I = 203,6 V ; W = E / K = 20,36 rd/s ;
n = 30.W/p = 194 tr/min
Tem = K.I = = -1 800 Nm ; Tu =Tem - Tr = -1 900 Nm
Cliquez ici |
2.14 |
La machine fonctionne au point M3 défini par n = -250 tr/min et Tu = 800 Nm. Quel est le quadrant de fonctionnement dans le plan n(Tu). Calculer la vitesse et le courant d'induit. |
n < 0 , Tu > 0 donc quadrant 4 (Générateur sens -)
Tem =Tu + Tr = 700 Nm car n < 0 impose Tr < 0
I = Tem / K = 70 A
E = K. W = E / K = -262 V ; U = E + R.I = -260 V
Cliquez ici |
2.15 |
La machine fonctionne au point M4 défini par n = -280 tr/min et Tu = -1 500 Nm. Quel est le quadrant de fonctionnement dans le plan n(Tu). Calculer la tension et le courant d'induit |
n < 0 , Tu < 0 donc quadrant 3 (Moteur sens -)
Tem = Tu + Tr = -1 600 Nm ( n < 0 donc Tr< 0);
I = Tem / K = -160 A
E = K. W = E / K = -293 V ; U = E + R.I = -296 V
Cliquez ici |
Etude de l'alimentation
La structure est commandée en logique d'inversion. |
2.20 |
En conduction continue, combien y-a-t-il de thyristors simultanément passants ? |
Dans la commande en logique d'inversion, un seul des deux ponts est commandé; il n'ya donc que 2 thyristors passants à chaque instant
Cliquez ici |
2.21 |
En conduction continue, donner les expressions des valeurs moyennes des tensions u' et u" en fonction de la tension efficace en ligne du réseau Ur "et des angles de commande, a' pour la structure PD'3 et a" pour la structure PD"3. |
Structure Pm : tension moyenne= (m/p).sin(p/m).Vmax.cosa
Structure PDm : tension moyenne= 2.(m/p).sin(p/m).Vmax.cosa
Structure PD'3 : U'= 2.(3/p).sin(p/3).Vmax.cosa' = (3.Ö3/p).Vmax.cosa'
U' = (3/p).Urmax.cosa' = (3.Ö2/p).Ur.cosa' = 1,35. Ur.cosa'
U" = 1,35. Ur.cosa"
Cliquez ici |
2.22 |
On respecte les butées de commande de 10° en redresseur et 150° en onduleur. Quelle est la valeur minimale de la tension Ur qui permet d'obtenir le fonctionnement de la question 2.11 ? pour la suite, on prendra Ur = 380 V |
La tension de chaque pont varie de 1,35. Ur.cos150° = -1,17.Ur
à 1,35. Ur.cos10 ° = 1,33.Ur . Comme U doit varier de -423 à 423 V, il faut Ur > 362 V dans le cas le plus défavorable
Cliquez ici |
2.23 |
On veut rester en conduction permanente pour |I| > 50 A. Montrer qu'il faut ajouter une inductance de filtrage Lf en série avec l'induit. Calculer la valeur de Lf. |
Aide |
La conduction est toujours continue pour
x = X.Imoy/ Urmax > 0,09 ; Il faut donc une réactance X = L.w > 0,97 W soit L > 3,1 mH
Il faut donc Lf > 3,1 - 0,4 = 2,7 mH
Cliquez ici |
Analyse du fonctionnement
On adopte les valeurs Ur = 380 V , L = Li + Lf = 5 mH et R = Ri + Rf = 25 mW
|
La machine fonctionne au point M1 défini au 2.12 |
2.30 |
Quel est le pont qui doit être commandé ? Calculer la valeur de son angle de comm
Pour un redresseur PDm, l'harmonique de rang k.m de la tension est :
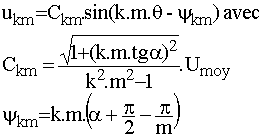
ande |
On doit avoir I > 0, donc on doit commander PD'3 en redresseur pour avoir U = U' > 0
U =1,35.Ur.cos a' = 513.cos a' = 250 V donc a' = 61°
Cliquez ici |
2.31 |
Calculer les harmoniques du courant d'induit |
Aide |
|
2.32 |
Calculer les puissances active, réactive, apparente et déformante fournies par le réseau en négligeant l'ondulation de i. |
P = Umoy.I = 27,5 kW
Q = P.tga' = 49,6 kVAR
Courant efficae en ligne Ir = I .Ö(2/3) = 98,8 A
Puissance apparente S = Ö3.Ur .Ir = 59,1 kVA
Puissance déformante : D = Ö(S² -P² -Q²) = 16,7 kVA
Cliquez ici |
La machine fonctionne au point M2 défini au 2.13 |
2.33 |
Quel est le pont qui doit être commandé ? Calculer la valeur de son angle de commande |
I < 0 donc il faut commander le pont PD"3
U" = - U < 0 donc la structure fonctionne en onduleur
U" = -200 V = 513.cos a" donc a" = 113 °
Cliquez ici |
2.34 |
Calculer le facteur de puissance du réseau en négligeant l'ondulation du courant i |
P" = U.I = -36 kW ; Ir = I" .Ö(2/3) = 147 A
S = Ö3.Ur .Ir = 96,7 kVA ; Fp = |P| / S = 0,37
Cliquez ici |
La machine fonctionne au point M3 défini au 2.14 |
2.35 |
Quel est le pont qui doit être commandé ? Calculer la valeur de son angle de commande |
I > 0 donc il faut commander PD'3 ; U' = U < 0 donc la structure fonctionne en onduleur
U = 513.cos a' = -260 V donc a' = 120°
Cliquez ici |
2.36 |
Calculer les puissances active, réactive, apparente et déformante fournies par le réseau en négligeant l'ondulation du courant i |
P = Umoy.I = -18,2 kW
Q = P.tga' = 31,5 kVAR
Courant efficae en ligne Ir = I .Ö(2/3) = 57 A
Puissance apparente S = Ö3.Ur .Ir = 37,6 kVA
Puissance déformante : D = Ö(S² -P² -Q²) = 9,5 kVA
Cliquez ici |
La machine fonctionne au point M4 défini au 2.14 |
2.37 |
Quel est le pont qui doit être commandé ? Calculer la valeur de son angle de commande |
On a I < 0, il faut donc commander PD"3 ; comme U < 0, U" > 0 donc la structure fonctionne en redresseur
U" = - U = 296 V = 513. cos a" donc a" = 55 °
Cliquez ici |
2.38 |
Décrire le mode opératoire pour passer du point M4 au point M3 |
On part avec PD"3 conduisant en redresseur avec a" = 55° et on doit arriver avec PD'3 conduisant aveca' = 120 °
On va d'abord augmenter a", la tension U = E + R.I tend vers 0 ; la vitesse et la f.é.m. varient beaucoup moins vite que le courant donc I tend vers 0.
Lorsqu'on détecte le zéro de i, on coupe la commande de PD"3 et on attend le blocage de tous les thyristors (1/3 de période)
On peut alors commander PD'3 avce un angle tel que U' = E = -293 V soit
a' = 125° puis on diminue a' jusqu'à 120°
Cliquez ici |