Exercice 1 : Redresseur P6 à thyrsitors
Le redresseur est alimenté par un réseau équilibré à six phases de valeur efficace
V = 50 V et de fréquence 50 Hz. La charge est formée de l'association en série d'une résistance R = 0,5W , d'une inductance L = 2 mH et d'une f.é.m. constante E = 24 V
Les tensions du réseau sont représentées sur la figure ci-dessous
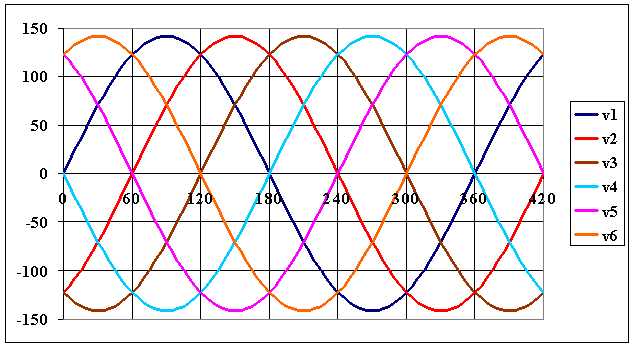
|
On néglige l'impédance de la source et on suppose les redresseurs parfaits |
1.1 |
Quelle est la condition nécessaire pour rester en conduction continue ? |
La condition est Umoy > E
Umoy= Ud.cos a avec Ud = (6/p)*sin(p/6).Vmax = 67,5 V
cos a > 0,355 soit a < 69 °
Cliquez ici |
1.2 |
Pour a = 30°, calculer l'intensité i(t) par la méthode directe |
T1 conduit de 90° à 150°
X = 0,63 W ; k = X/R =1,26 ; Z = 0,8 W ; j = 51,5° ; I2max = Vmax/Z =88,1 A
i = A.exp(-q/k) +88,1sin(q-j) -48
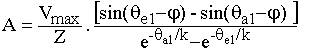 = 199,1 A = 199,1 A
On peut vérifier que i(qa1) = 64 A > 0 donc que la conduction est continue
Cliquez ici |
1.3 |
Pour a = 45°, calculer l'intensité i(t) par la méthode harmonique |
|
1.4 |
La méthode du premier harmonique est-elle applicable ? |
Non car l'harmonique de rang 12 de i n'est que 4 fois plus faible que celui de rang 6
Cliquez ici |
1.5 |
Pour a = 45°, calculer les valeurs moyennes et efficaces de i |
|
1.6 |
Pour a = 70°, calculer l'intensité i(t) et l'angle b où T1 se bloque |
Pour cette valeur de a, on est en conduction interrompue
T1 conduit de 130° à b.
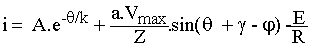 avec a = 1 et g = 0 avec a = 1 et g = 0
X = 0,63 W ; k = X/R =1,26 ; Z = 0,8 W ; j = 51,5° ; I2max = a.Vmax/Z =88,1 A
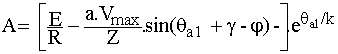 = -233 A = -233 A
Par approximations successives, on calcule b = 182,5 °
Cliquez ici |
1.7 |
Pour le fonctionnement précédent, calculer les valeurs moyennes de u et i |
Umoy = 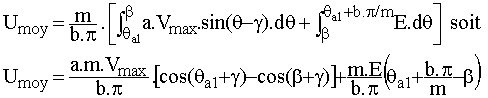
Avec b = 2, Umoy = 27,1 V et Imoy = (Umoy - E) / R = 6,1 A
Cliquez ici |
Pour a = 30°, on suppose le courant parfaitement lissé de valeur moyenne
I = 70 A
|
|
L'inductance de la source alternative est Ls = 200 µH. En déduire l'angle d'empiétement |
cos(a) - cos(a+µ) = m.Xs.I/p.Ud donne µ = 12,1 °
Cliquez ici |
1.9 |
Quele est le nombre de thyristors passants durant l'empiétement ? |
Chaque thyristor conduit pendant 60° et l'angle d'empiétement
µ = 12 ° < 60 ° donc il y a deux thyristors passants simultanément
Cliquez ici |
1.10 |
Calculer la chute de tension due à l'empiétement |
Duemp = m.Xs.I/2.p = 4,2 V
Cliquez ici |
1.11 |
Chaque redresseur a une tension de seuil VF = 0,8 V et une résistance RF = 0,01 W. Calculer la chute de tension due aux redresseurs |
DUF = VF - RF.I.(1-m.µ/4.p) = 1,4 V
Cliquez ici |
Exercice 2 : Montage P3
Le redresseur est alimenté par un réseau équilibré de valeur efficace V = 230 V et de fréquence f = 50 Hz .
La charge est un moteur à courant continu excité par des aimants permanents.
On donne :
induit : résistance R = 0,5 W , inductance L = 500 µH
constante de flux : K = f.é.m. / vitesse en rd/s = 0,8 Vs
courant absorbé à vide : 1 A
couple de pertes négligé
|
La machine entraîne une charge de couple résistant constant
Tr = 15 Nm
L'angle de retard à l'amorçage est réglé à la valeur a = 60°
On utilise les courbes de charges du montage P3 disponibles en cliquant ici
|
2.1 |
Calculer l'intensité moyenne I |
Le couple moteur Tu = Tr, comme on néglige le couple de pertes
Tr = Tem = K.I donc I = 25 A
Cliquez ici |
2.2 |
Montrer que la conduction est interrompue |
Pour a = 60 °, la valeur critique de x permettant la conduction continue est de l'ordre de 0,28. x = X.I/Vmax ; X = L.w = 157 mW ; Vmax = 325 V donc
x = 0,000 48.I
Pour I = 25 A , x = 0,012< x critique
Cliquez ici |
2.3 |
Déterminer la valeur moyenne de u et la vitesse |
Pour x = 0,012, et a = 60 °, y est de l'ordre de 0,87 donc Umoy = y.Vmax = 283 V
E = U - R.I = 270 V = K. W ; n = 30.W/p = 3 230 tr/min
Cliquez ici |
2.4 |
Calculer la durée de conduction d'un thyristor |
T1 conduit de 90° à b.
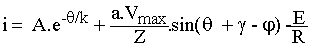 avec a = 1 et g = 0 avec a = 1 et g = 0
X = 0,16 W ; k = X/R =0,32 ; Z = 0,52 W ; j = 17,44° ; I2max = a.Vmax/Z = 620,6 A
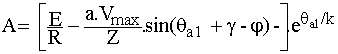 = -7 732A = -7 732A
Par approximations successives, on calcule b = 136,2 °
Cliquez ici |
Pour rester en conduction continue pour tout fonctionnement, on ajoute une inductance de filtrage Lf en série avec l'induit du moteur. |
2.5 |
Quelle est la valeur minimale de Lf ? Pour la suite, on prendra L' = L + Lf = 500 mH |
On est en conduction continue si x < xcr ; dans le cas le plus défavorable xcr = 0,325
il faut donc (Xf+X) . I /Vmax > xcr soit Xf+X > xcr.Vmax / I
Avec I min = 1 A , il faut Xf+X > 105,7 W soit Lf + L / > 336 mH
Lf > 335,5 mH
Cliquez ici |
2.6 |
La machine fonctionne en moteur avec une vitesse n = 2 000 tr/min et un couple utile de moment Tu = 10 Nm. Calculer l'angle de retard à l'amorçage et l'ondulation du courant d'induit |
Dans une machine continue Tu = Tem - Tp = K.I -Tp et U = E + R.I avec E = K.W
Pour le calcul de l'ondulation utiliser la méthode harmonique
Aide |
Tem = Tu = 10 Nm ; I = Tem / K = 12,5 A ; E = K.W = 167,6 V ; U = E + R.I = 173,8 V
cos a = U/Ud avec Ud =(3/p).sin(p/3).Vmax = 269 V , cos a = 0,646 ; a = 49,8 °

L'harmonique de rang 6 étant plus de 4 fois plus faible que celui de rang 3, on peut utiliser l'approximation du premier harmonique donc Dicàc = 2.I3max = 0,68 A
Cliquez ici |
2.7 |
L'angle de retard à l'amorçage est a = 120 ° et le moment du couple utile est Tu = 8 Nm. Calculer la vitesse et l'ondulation du courant d'induit |
Tem = Tu = 8 Nm ; I = Tem / K = 10 A ; U = Ud . cos a = -134,5 V
E = U - R. I = K.W = -139,5 V ; n = - 1 665 tr/min

L'harmonique de rang 6 étant plus de 4 fois plus faible que celui de rang 3, on peut utiliser l'approximation du premier harmonique donc Dicàc = 2.I3max = 0,76 A
Cliquez ici |
Exercice 3 : Montage PD2
Le redresseur est alimenté par un réseau équilibré de valeur efficace V = 48 V et de fréquence f = 50 Hz .
La charge est une batterie de f.é.m. E = 24 V et de résistance interne r = 0,2 W.
On place en série une bobine d'inductance L et de résistance
r' = 0,1W. On pose R = r + r'.
|
3.1 |
Comment doit-on choisir l'inductance L pour que la conduction soit continue pour
a < 45 ° ?
|
Utiliser la caractéristique de charge du montage PD2 identique à celle du montage P2
Cette caractéristique est donnée à la fin du cours
Aide |
Pour a = 45 °, xcr = 0,45
U = (2.Vmax /p) . cos a = 30,6 V
I = (U-E/R) = 21,9 A
x = X.Imoy / Vmax soit X = 0,45. Vmax /Imoy = 1,4 W et L = X /(2.p.f) = 4,45 mH
Cliquez ici |
3.2 |
Pour a = 30°, calculer l'intensité i(t) par la méthode harmonique |
Pour a = 30°, la conduction est continue
Umoy = (2.Vmax /p) . cos a = 37,4 V ; Imoy = (Umoy-E/R) = 44,8 A
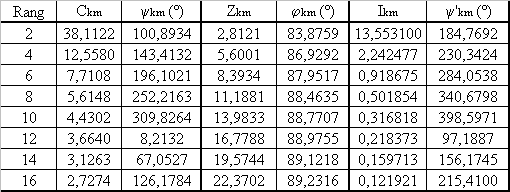
Cliquez ici |
3.3 |
Pour a = 60°, calculer l'intensité i(t) et la tension moyenne aux bornes de la charge |
T1 et T'2 sont amorcés en a = 60°; la conduction est discontinue donc ces deux thyristors se bloquent en b < 240 °
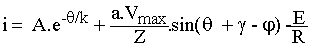 avec a = 2 et g = 0 avec a = 2 et g = 0
Vmax = 24.Ö2 =33,9 V ; X = 1,40 W ; k = X/R =4,66 ; Z = 1,43 W ; j = 77,9° ;
I2max = a.Vmax/Z = 23,7 A
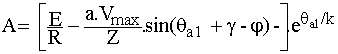 = 118 A = 118 A
Par approximations successives, on calcule b = 221,3°
Umoy = 29,5 V
Cliquez ici |
3.4 |
Pour a = 0°, on néglige l'ondulation de i mais on tient compte de l'impédance de la source modélisée par une inductance Ls = 100 µH. Calculer la tension et l'intensité moyennes dans la charge. |
Umoy = Uid - DUemp = 2.Vmax/p - + R.Imoy
Uid = 43,2 V ; Imoy = 60 A ; DUemp =1,2 V ; Umoy = 42 V
Cliquez ici |
3.5 |
Calculer la durée de l'empiétement |
Avec a = 0, il vient 1 - cosµ = 4.Xs.Imoy/p. Ud soit µ = 19,2 °
Cliquez ici |
3.6 |
Combien de thyristors sont passants durant l'empiétement ? |
T1 et T'2 sont amorcés en a = 0° alors que T2 et T'2 sont passants
On a donc les quatre thyristors simultanément passants
Cliquez ici |