Les bases de Windows XP

Électronique de puissance

xxxxxxModule 5 : xxxxxxx "Conversion AC - DC "

Chapitre 5.1

Structures de conversion

Choix : cliquez sur la flèche

Structure P6 à diodes

Structure P4 à thyristors

Structure PD6

*Exercice 1 : Redresseur P6 à diodes* *Le redresseur est alimenté par un réseau équilibré à six phases de valeur efficace* *V = 130 V. La charge absorbe un courant constant I = 150 A.* *Les tensions du réseau sont représentées sur la figure ci-dessous*
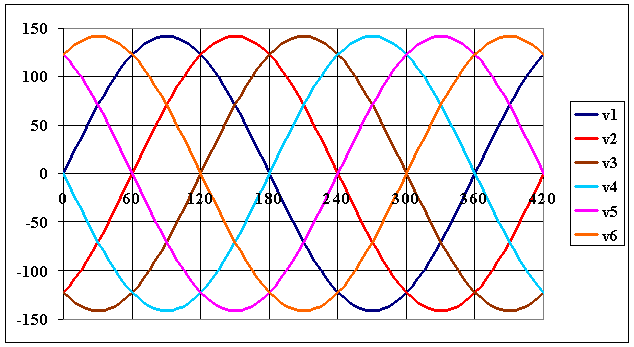
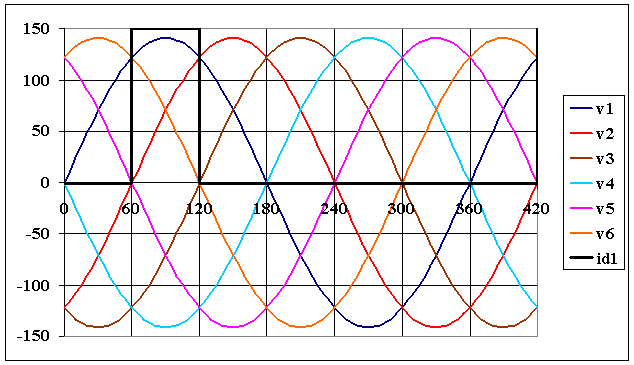
1.1	Déterminer les intervalles de conduction de chacune des six diodes	Dk conduit lorsque vk est la plus grande des six tensions D1 conduit de 60 à 120° , D2 de 120 à 180°, D3 de 180 à 240°, D4 de 240 à 300°, D5 de 300 à 360 °et D6 de 360 à 420° donc de 0 à 60° Cliquez ici
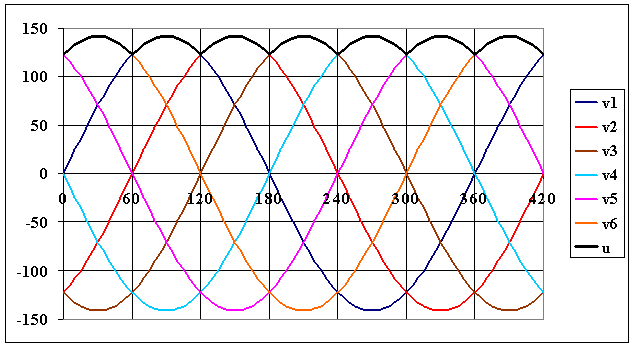
1.2	Représenter la tension u en sortie du redresseur	Lorsque Dk conduit, u = vk : Cliquez ici
1.3	Calculer la valeur moyenne de u	Umoy = (6/p).sin(p/6).Vmax , avec Vmax = V.Ö2, Umoy = 135 V Cliquez ici
1.4	calculer l'ondulation crête à crête de u	Umin = v1(p/3) = Vmax.sin(p/3) = 122,5 V Umax = Vmax = 141,4 V Du = 18,9 V Cliquez ici
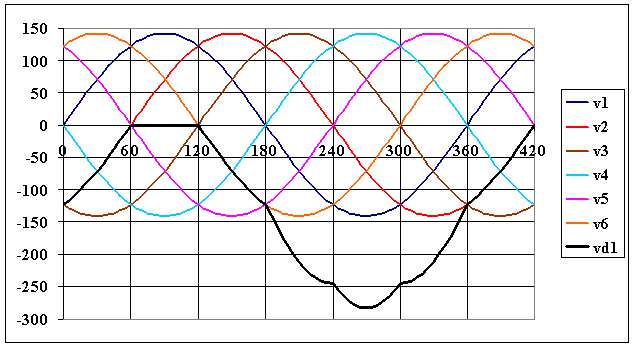
1.5	représenter la tension vd1 aux bornes de la diode D1	vd1 = v1 - u Cliquez ici
1.6	calculer les valeurs moyenne et efficace du courant dans un fil de ligne	Jmoy = I / 6 = 25 A ; Jeff = I / Ö6 = 61,2 A Cliquez ici
1.7	calculer le facteur de puissance du réseau AC	S = 6.V.Jeff = 36,74 kVA ; P = Umoy.I = 20,25 kW Fp = P / S = 0,55 Cliquez ici
*Exercice 2 : Structure P4 à thyristors* *Le redresseur est alimenté par un réseau équilibré à quatre phases de valeur efficace* *V = 230 V. La charge absorbe un courant constant I = 200 A.* *Les tensions du réseau sont représentées sur la figure ci-dessous*
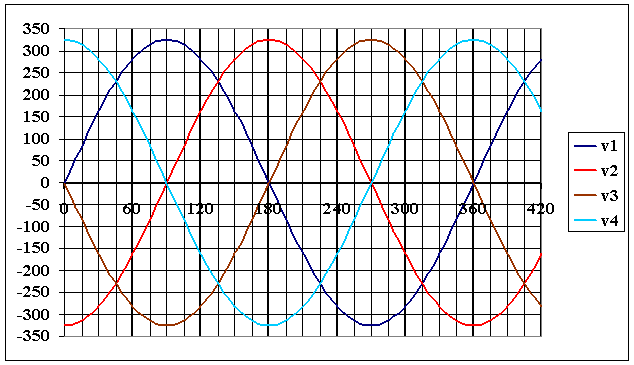
2.1	Les thyristors sont amorcés avec un angle de retard a = 90° . déterminer les intervalles de conduction des quatre thyristors et en déduire la graphe de u(t)	Th1 devient amorçable lorsque v1 est la plus grande des tensions soit en 45° ; compte tenu du retard de 90°, il s'amorce en 135° Th2 devient amorçable lorsque v2 est la plus grande des tensions soit en 135° ; compte tenu du retard de 90°, il s'amorce en 225° Th3 devient amorçable lorsque v3 est la plus grande des tensions soit en 225° ; compte tenu du retard de 90°, il s'amorce en 315° Th4 devient amorçable lorsque v4 est la plus grande des tensions soit en 315° ; compte tenu du retard de 90°, il s'amorce en 405° = 45° 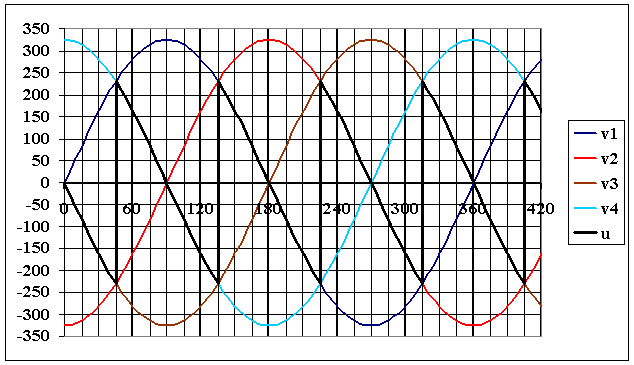Cliquez ici
2.2	Exprimer la tension moyenne de sortie en fonction du retard a.	Ud = (4/p).sin(p/4).Ö2.V = 292,8 V Umoy = Ud . cos a Cliquez ici
2.3	calculer les valeurs moyenne et efficace du courant dans un fil de ligne	Jmoy = I / 4 = 50 A ; Jeff = I / Ö4 = 100 A Cliquez ici
2.4	Pour a = 30°, calculer les puissances active, réactive, déformante et le facteur de puissance du réseau AC	Umoy = Ud.cosa = 254 V ; P = Umoy . I = 50,7 kW Q = P.tga = 29,3 kVAR ; S = 4.V.Jeff = 92 kVA D = Ö(S² - P² - Q²) = 70,9 kVA ; Fp = P /S = 0,55 Cliquez ici
2.5	Pour a = 120°, calculer les puissances active, réactive, déformante et le facteur de puissance du réseau AC	Umoy = Ud.cosa = -146 V ; P = Umoy . I = -29,3 kW Q = P.tga = 50,7 kVAR ; S = 4.V.Jeff = 92 kVA D = Ö(S² - P² - Q²) = 70,9 kVA ; Fp = \|P\| /S = 0,32 Cliquez ici
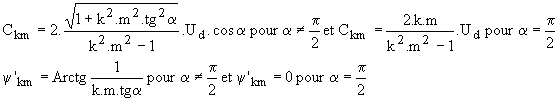
2.6	Pour a = 30°, calculer le fondamental de la décomposition en série de Fourier de la tension u	Le fondamental est de fréquence 4 . Pour k = 1, on a C4 = 136,7 V Cliquez ici
*Exercice 3 : Montage PD6* *Le redresseur est alimenté par un réseau équilibré à six phases de valeur efficace* *V = 400 V. La charge absorbe un courant constant I = 800 A.* *Les tensions simples du réseau sont représentées sur la figure ci-dessous*
3.1	déterminer en fonction de a, l'angle d'amorçage et l'angle de blocage des thyristors T1 et T'1 connectés à la phase 1	T1 s' amorce en q_a1= p/2 - p/m + a = 60 + a et conduit pendant un angle de 2.p/m =60° T'1 s' amorce en q'_a1= q_a1+p = 240 + a et conduit pendant un angle de 2.p/m =60° Cliquez ici
3.2	Pour a = 30°, représenter la tension u(t)	Cliquez ici
3.3	exprimer la tension moyenne de sortie en fonction du retard a.	Ud = 2.(6/p).sin(p/6).Ö2.V = 1 080 V Umoy = Ud . cos a Cliquez ici
3.4	calculer les valeurs moyenne et efficace du courant dans un fil de ligne	*Jmoy = 0 = 50 A ; Jeff = I Ö(2/6) = 462 A** Cliquez ici
3.5	Pour a = 60°, calculer les puissances active, réactive, déformante et le facteur de puissance du réseau AC	Umoy = Ud.cosa = 540 V ; P = Umoy . I = 432 kW Q = P.tga = 749 kVAR ; S = 6.V.Jeff = 111 kVA D = Ö(S² - P² - Q²) = 694 kVA ; Fp = P /S = 0,39 Cliquez ici
3.6	Pour a = 150°, calculer les puissances active, réactive, déformante et le facteur de puissance du réseau AC	Umoy = Ud.cosa = -936 V ; P = Umoy . I = -749 kW Q = P.tga = 432 kVAR ; S = 4.V.Jeff = 111 kVA D = Ö(S² - P² - Q²) = 694 kVA ; Fp = P /S = 0,68 Cliquez ici