1 principe de la commutation douce
Dans les montages hacheurs et les alimentations à découpage, on cherche à travailler à la fréquence de découpage f la plus grande possible afin de minimiser le volume des circuits magnétiques et des éléments de filtrage. On est cependant limité par les phénomènes induits par les commutations des interrupteurs.
Dans les structures étudiées précédemment, on travaille en commutations dures forcées par la commande; l'allure des grandeurs de l'interrupteur commandé est donnée par la fig.1 :
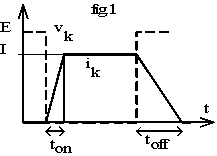
Ce type de commutation crée :
Ø des pertes de commutation de valeur 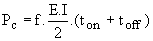
Ø des surtensions importantes dues aux inductances parasites et aux inductances de fuites, proportionnelles au gradient de courant dik/dt
Ø des perturbations électromagnétiques conduites vers la source et rayonnées par le convertisseur.
Tous ces phénomènes s'aggravent lorsque la fréquence de commutation augmente.
Pour limiter ces inconvénients, on doit adopter des commutations douces, consistant à commuter l'interrupteur lorsque l'intensité ou la tension est nulle (fig.2) :
Commutation ZSC |
|
Commutation ZVS |
Comme les structures hacheur fonctionnent avec une source et une charge de type continu, la commutation douce exige l'utilisation de circuits résonnants L-C.
En associant interrupteur et circuit résonnant, on crée des interrupteurs dits résonnants permettant de réduire fortement les pertes de commutation et de limiter les gradients de courant.
2 commutation à zéro de courant
2.2 Interrupteur unidirectionnel en courant
Examinons les commutations du circuit de la fig.3 : 
L'interrupteur K est unidirectionnel en courant et commandé à la fermeture; il est associé au circuit résonnant L-C; la diode D assure la continuité du courant Is supposé constant lorsque K est ouvert.
En t = 0-, K est ouvert et le régime permanent de blocage est atteint. D conduit donc vd = 0 et id = Is;
u = v = E ; i = j = 0.
A t = 0 on commande la fermeture de K.
A t = 0+, v = 0; C impose u = 0 et L impose i = 0; D conduit; Id = Is et j = 0.
Ø Première phase : tant que i n'a pas atteint la valeur Is, D conduit pour assurer la continuité du courant de charge donc v = E = Cste et j = 0; on a donc L.di/dt = E soit i = E.t/L et Id = Is - E.t/L. Cette phase prend fin avec le blocage de D pour Id = 0 en t1 = L.Is/E.
Ø Deuxième phase : en t1+, D est bloquée. i + j = Is = Cste; j = C.du/dt ; u = L.di/dt. Nous en déduisons : di/dt = -dj/dt soit u = -L.C.d²u/dt². Posons t' = t - t1 et w =1/Ö(L.C); il vient :
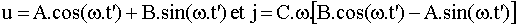
Avec les conditions initiales u = E et j = 0, nous obtenons : A = E et B = 0; nous en déduisons :
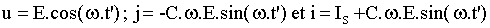
Posons k = Is/C.w.E, il vient i = Is.[1+(1/k).sin(w.t')]; Pour que l'interrupteur se bloque à zéro de courant, il faut que l'amplitude de l'oscillation soit supérieure au courant charge soit 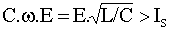 soit k < 1; il existe alors un instant t'2 avec p < w.t'2 < 3.p/2 tel que i(t'2)= 0; il vient : soit k < 1; il existe alors un instant t'2 avec p < w.t'2 < 3.p/2 tel que i(t'2)= 0; il vient :
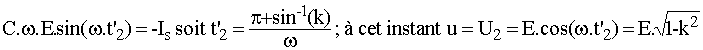
Ø Troisième phase : la passage à zéro de i provoque le blocage naturel de K.
vd(t'2) = U2- E < 0 donc D reste bloquée et i = Id = 0 donc j = Is = Cste; la condensateur se charge donc à courant constant. En posant t" = t-t2, il vient j = C.du/dt et u = U2+Is.t"/C. vd = U2-E+Is.t"/C devient nulle en t"3 tel que t"3 = C.(E-U2)/Is
A cet instant, C est chargé sous la tension E et on retrouve les conditions initiales.
La fig.4 donne l'allure des grandeurs : 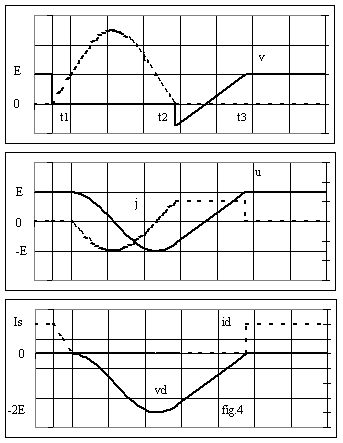
On constate :
v l'annulation des pertes de commutation de K
v la limitation du gradient de courant par l'inductance L, ralentit la décroissance du courant dans D donc diminue le courant de recouvrement inverse; en outre, il est plus facile d'assurer la protection en courant des interrupteurs.
v l'oscillation de courant crée une surintensité dans l'interrupteur, le courant i dépassant la valeur 2.Is.
v l'augmentation de la tension inverse aux bornes de D (-2.E au lieu de E).
2.3 Interrupteur bidirectionnel en courant
Sur le schéma de la fig.3, on ajoute une diode D' tête-bêche avec l'interrupteur K.
Le fonctionnement est semblable. Dans la phase 2, le courant i peut devenir négatif donc K ne se bloque pas en t'2 mais lorsque le courant i, après s'être inversé à travers D', redevient nul; l'instant de blocage est donc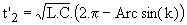
2.4 Exemple d'utilisation
On étudie la structure représentée par la figure ci-contre :
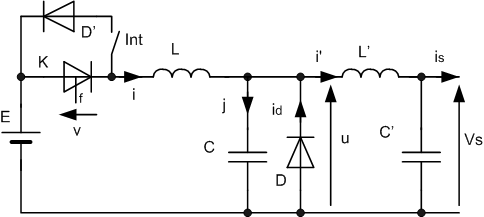
On retrouve la structure d'une alimentation de type Buck. L'interrupteur Int permet de faire fonctionner l'interrupteur résonnant en mode unidirectionnel (Int ouvert) ou bidirectionnel (Int fermé).
Pour simplifier l'étude, on considèrera que
v le filtrage en sortie par L' et C' est parfait : on néglige donc l'ondulation de vs de is et de i'; on a donc i'(t) = Is = Cste.
v les interrupteurs sont parfaits; K est commandé à la fermeture et s'ouvre naturellement lorsque le courant qui le trasverse s'annule
Interrupteur unidirectionnel
Supposons que la diode D' est déconnectée
è Etat initial : à t = 0- , K est ouvert donc D conduit ; i(0-) = j(0-) = 0 ; id(0-) = Is ; u(0-) = 0
è Phase 1 : à t = 0, on commande la fermeture de K imposant v = 0 ; i ne peut être discontinu et C ne peut fournir i' car il est déchargé; la diode D continue à conduire donc u = 0. Le condensateur C reste déchargé donc j = 0.
L.di/dt = E - v - u = E donc i = E.t/L et id = i' - i = Is - E.t/L
Cette phase prend fin par le blocage de K ou de D. Le courant dans K étant croissant, il ne peut se bloquer donc la phase se termine en t1 par le blocage de D lorsque id = 0 soit en t1 = L.Is / E; on a alors i(t1) = Is
è Phase 2 : à t = t1, K est fermé et D est bloquée; le circuit L-C va entrer en oscillation
E = L.di/dt + u , j = C.du/dt et i = j + Is ; on en déduit di/dt = dj/dt = C.du²/dt² ; la tension u évolue suivant l'équation L.C.du²/dt² + u = E

Cette phase prend fin par le blocage de K ou la remise en conduction de D si u s'annule avant i.
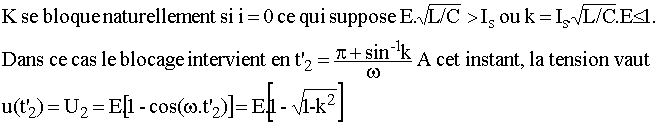
è Phase 3 : à t = t2, K est bloqué et u > 0 donc D ne peut conduire; le condensateur va alimenter la charge en se déchargeant à courant constant Is.
u = u2 - Is.t"/C avec t" = t - t2. Cette phase se termine par la mise en conduction de D lorsque u = 0 soit en t"3 = C.u2/Is.
On retrouve alors l'état initial qui se maintient jusqu'à la fermeture de K.
La figure ci-dessous donne l'allure des graphes :

Calculons la tension moyenne en sortie; la valeur moyenne de la tension aux bornes d'une inductance étant nulle, Vsmoy = Umoy.
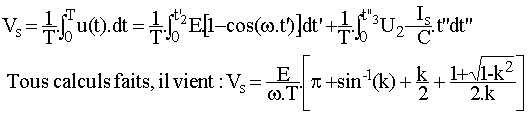
Le coefficient k est fixé par les composants du circuit résonnant, la tension d'alimentation E et le courant de charge. Pour une charge donnée, la tension moyenne ne peut varier qu'avec la période de découpage T et pour une fréquence de découpage fixe, la tension moyenne varie avec la charge.
L'utilisation d'un interrupteur résonnant unidirectionnel en courant est peu fréquente car la réglage de la tension de sortie est fortement dépendant de la charge. De plus le courant maximal dans l'interrupteur doit être au moins égal à 2.Is soit le double de celui que l'on aurait sans résonance. Le coefficient de dimensionnement de l'interrupteur K est donc au moins deux fois plus grand pour l'interrupteur résonnant que pour la structire classique.
Interrupteur bidirectionnel
Connectons la diode D' :
è Etat initial : à t = 0- , K est ouvert donc D conduit ; i(0-) = j(0-) = 0 ; id(0-) = Is ; u(0-)
è Phase 1 : à t = 0, on commande la fermeture de K imposant v = 0 ; i ne peut être discontinu et C ne peut fournir i' car il est déchargé; la diode D continue à conduire donc u = 0. Le condensateur C reste déchargé donc j = 0.
Cette phase est indetique à celle étudiée pour l'interrupteur unidirectionnel; elle prend fin avec le blocage de la diode D en t1
è Phase 2 : à t = t1, K est fermé et D est bloquée; le circuit L-C va entrer en oscillation
E = L.di/dt + u , j = C.du/dt et i = j + Is ; on en déduit di/dt = dj/dt = C.du²/dt² ; la tension u évolue suivant l'équation L.C.du²/dt² + u = E

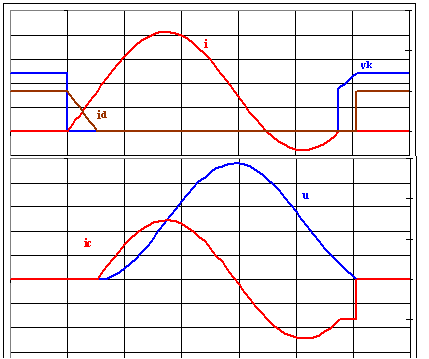
Le courant i est d'abord positif puis s'annule en 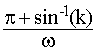 ; l'interrupteur K se bloque; à cet instant la tension u est positive donc D reste bloquée; c'est la diode D' qui devient passante; cette phase va donc se poursuivre avec un courant i négatif et prend fin par le blocage de D' lorsque i s'annule de nouveau en ; l'interrupteur K se bloque; à cet instant la tension u est positive donc D reste bloquée; c'est la diode D' qui devient passante; cette phase va donc se poursuivre avec un courant i négatif et prend fin par le blocage de D' lorsque i s'annule de nouveau en
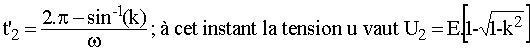
è Phase 3 : à t = t2, K est bloqué et u > 0 donc D ne peut conduire; le condensateur va alimenter la charge en se déchargeant à courant constant Is.
u = u2 - Is.t"/C avec t" = t - t2. Cette phase se termine par la mise en conduction de D lorsque u = 0 soit en t"3 = C.u2/Is.
On retrouve alors l'état initial qui se maintient jusqu'à la fermeture de K.
La figure ci-dessous donne l'allure des graphes
La tension moyenne de sortie a alors pour expression : 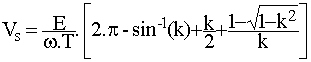
Pour k variant de 0,1 à 0,99 la variation de Vsmoy n'est que de 1,1 %, et la tension de sortie est 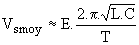 . .
La tension de sortie devient alors quasiment indépendante de la charge.
è Les interrupteurs commutant au zéro de courant peuvent être utilisés dans :
Ø les alimentations non isolées de type Buck (abaisseur de tension) ou Buck-Boost (inverseur de tension); dans ce cas le circuit résonnant L-C doit être ajouté à la structure
Ø les alimentations isolées de type Flyback ou Forward : l'inductance L est alors l'inductance de fuites du transformateur et le condensateur C est placé au secondaire du transformateur
Ø diminution des pertes de commutation
Ø diminution des surtensions dues aux inductances parasites lorsque celles-ci sont utilisées dans le circuit résonnant
Ø diminution des perturbations rayonnées par le circuit
Ø tension de sortie fortement dépendante du courant de charge pour les interrupteurs résonants unidirectionnels en courant
Ø impossibilité de fonctionner à vide pour les interrupteurs unidirectionnels : dans ce cas il n'y a plus de résonance donc l'interrupteur ne se bloque pas.
Ø nécessité de fonctionner à fréquence variable pour régler la tension moyenne de sortie puisque la durée de conduction de l'interrupteur n'est plus commandée mais fonction uniquement des composants du circuit résonant.
Ø complexité plus grande de la commande : aux fréquences élevées utilisées dans ces montages les interrupteurs commandés ne peuvent être que des transistors MOS; or ceux-ci doivent être commandés à la fermeture mais aussi à l'ouverture; il faut donc détecter l'annulation du courant dans l'interrupteur pour commander l'ouverture à cet instant.
Ø la résonance augmente le courant maximal dans l'interrupteur commandé. Il faut un coefficient de dimensionnement théorique au moins deux fois plus grand avec un interrupteur résonant; cependant la réduction des surtensions créées par les inductances parasites permet de choisir une tension maximale de blocage plus faible, ce qui réduit le facteur réel de dimensionnement.
Ø les transistors de type MOS possèdent d'importantes capacités parasites; au blocage le courant est nul mais la tension varie rapidement; il peut alors apparaître des oscillations parasites créées par l'inductance de résonance et ces capacités.
3 Commutation au zéro de tension
3.1 Interrupteur unidirectionnel en courant
La cellule de commutation utilisée est représentée sur la fig.7 : 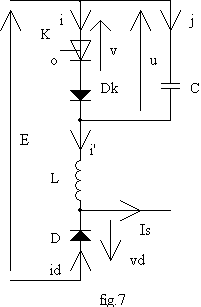
L'interrupteur K est unidirectionnel en courant; il est commandé à l'ouverture et s'amorce naturellement sous tension nulle. La diode Dk permet de bloquer une tension négative. Le courant Is est supposé constant.
Supposons qu'à t = 0-, K conduise depuis assez de temps pour que le régime permanent soit atteint :
v = u = 0 ; vd = - E ; i = i' = Is ; j = Id = 0.
A t = 0, on commande l'ouverture de K.
Ø Première phase : à t = 0+, K est ouvert donc i = 0 ; la tension v ne pouvant être discontinue, v = 0 donc D est bloquée et j = i' = Is. Le condensateur C se charge donc à courant constant u = Is.t/C ; L.di'/dt = 0 ; vd = Is.t/C-E. En t1 = C.E/Is, la tension vd s'annule donc D conduit.
Ø Deuxième phase : le circuit LC entre en oscillation, soumis à l'échelon de tension E.
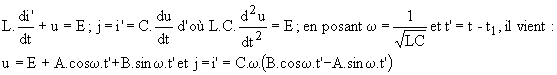
Les conditions initiales j = i' = Is et u = E donnent A = 0 et B=Is/C.w.
Posons k = L.w.Is/E = Is/C.w.E, nous obtenons u = E.(1+k.sinw.t') et i' = j = Is.cosw.t'.
Si k > 1, la tension u passe par un maximum E.(1+k) puis s'annule et devient négative.
Le courant i' étant alors négatif, Dk reste bloquée et l'oscillation se poursuit avec u < 0.
u s'annule de nouveau en t'2 tel que 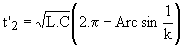 ; à cet instant on a ; à cet instant on a 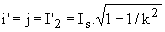 . .
Ø Troisième phase : la tension u étant nulle, Dk peut conduire et K s'amorce spontanément sous tension nulle. La tension u reste nulle. En t2, Id = Is-I'2 > 0 donc D conduit. L.di'/dt = E donc le courant i' augmente; en posant t" = t-t2, il vient i'=E.t"/L+I'2 et Id = Is-I'2-E.t'/L; ce courant s'annule en t"3 = L.(Is-I'2)/E.
On retrouve alors la phase initiale.
La fig.8 donne l'allure des grandeurs : 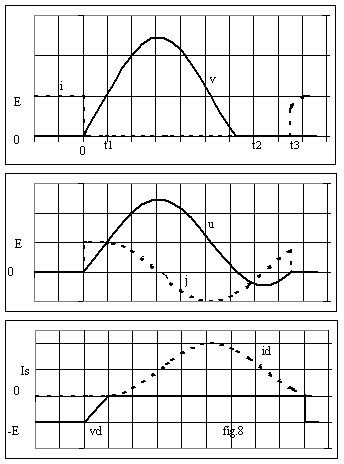
3.2 Interrupteur bidirectionnel en courant
Sur le montage de la fig.7, la diode Dk est placée, non plus en série avec K, mais tête-bêche en parallèle sur K. On a alors u = v et cette tension ne peut être négative. La phase 1 est identique à celle du montage unidirectionnel en courant. La phase 2 est régie par les mêmes équations mais se termine lorsque u s'annule avant de devenir négative donc en 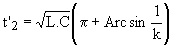 . .
On a alors 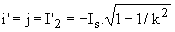 . Durant la phase 3, le courant i' augmente; en posant t" = t-t2, il vient i'=E.t"/L+I'2 et ID = Is-I'2-E.t'/L; le courant i = i' s'annule en t"3 = -L.I'2/E; à cet instant, Dk se bloque et K conduit. La phase prend fin par le blocage de D lorsque ID = 0 soit en t"4 = L.(Is-I'2)/E. . Durant la phase 3, le courant i' augmente; en posant t" = t-t2, il vient i'=E.t"/L+I'2 et ID = Is-I'2-E.t'/L; le courant i = i' s'annule en t"3 = -L.I'2/E; à cet instant, Dk se bloque et K conduit. La phase prend fin par le blocage de D lorsque ID = 0 soit en t"4 = L.(Is-I'2)/E.
Pour les deux types d'interrupteurs, la nécessité d'avoir k > 1 interdit le fonctionnement à vide ou à faible charge (Is » 0).
La résonance en tension crée une surtension k.E > E aux bornes de l'interrupteur.
Au blocage de D, la tension E est brutalement appliquée en inverse aux bornes de D; ce mode de blocage est peu favorable pour la diode et peut créer des oscillations parasites.
3.3 Exemple : utilisation dans un hacheur série
La structure est celle de la fig.7. La tension de sortie du hacheur est vs = -vd.
De 0 à t1, vs = vd = E-Is.t/C . De t1 à t3, vs = 0 et de t3 à T, vs = E. D'après la fig.8, la tension moyenne est Vsmoy = E.t1/(2.T)+E.(T-t3)/T.
Avec 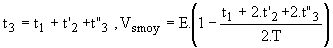
En mode unidirectionnel en courant, il vient :
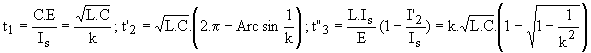 . .
Nous en déduisons
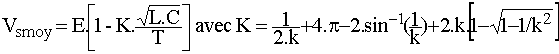 . .
K dépend de k donc du courant moyen Is dans la charge. A courant constant, la tension moyenne est fixée par la fréquence de découpage. Lorsque k varie de 1 à 5, le coefficient K varie de 12,42 à 12,57; on constate donc que la tension moyenne est quasi indépendante du courant de charge.
En mode bidirectionnel en courant :
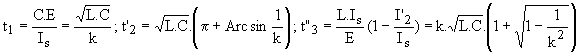
Nous en déduisons
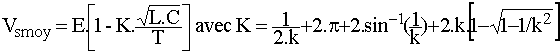 . .
Pour k variant de 1 à 5, K varie de 12,42 à 25,68. Dans ce cas, la tension de sortie varie avec le courant de charge.
D'autres types d'interrupteurs résonants peuvent être utilisés :
Ø l'interrupteur multirésonant combine la résonance en tension et la résonance en courant en plaçant un condensateur en parallèle sur K et un autre en parallèle sur le dipôle K+ inductance de résonance. Le fonctionnement est complexe mais ce type d'interrupteur permet le fonctionnement à vide.
Ø les interrupteurs résonants bicommandés permettant de commander ouverture et fermeture; l'emploi de ces interrupteurs dans les hacheurs permet de régler le transfert d'énergie en fonctionnant à fréquence fixe et rapport cyclique variable.
|