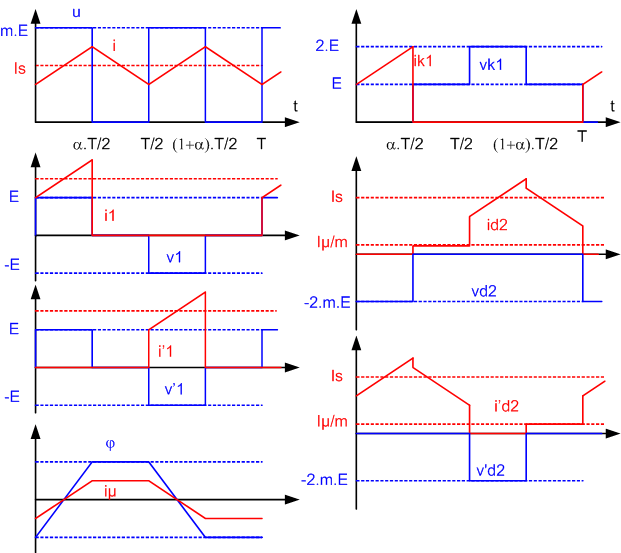
Première phase : K1 est fermé
|
è K1 fermé impose vk1 = 0 donc v1 = E; le transformateur impose v'1 = v1 et v2 = v'2 = -m.E è la continuité de i impose que D2 et/ou D'2 conduisent en permanence; il faut donc m.E > Vs è La diode D'2 est polarisée en direct donc est passante; la diode D2 est polarisée en inverse donc est bloquée è i2 = 0 ; i'2 = i ; i1 = m.i ; i'1 = 0 è le courant dans l'inductance croît suivant la loi i = (m.E-Vs).t/L + Imin |
 |