Électronique de puissance
xxxxxxModule 4 : xxxxxxx "Alimentations continues " |
Chapitre 4.5
Alimentations symétriques |
On étudie une alimentation de type push-pull réalisée suivant le schéma ci-dessous :
On donne : è la tension d'alimentation E = 24 V ± 30 % è la tension de sortie : Vs = 5 V ; ondulation DVscàc £ 10 mV è la puissance de sortie : Ps £ 100 W è fréquence de découpage : f = 100 kHz è le rendement estimé: h = 80 % è la valeur maximale du rapport cyclique : a = 40 % è l'ondulation crête à crête du courant dans l'inductance Di= 2 A è les caractéristiques des circuits magnétiques : cliquez ici pour ouvrir le fichier au format pdf (documentation ferroxycube)
|
|||
1. Dimensionnement |
|||
1.1 |
Calculer le rapport de transformation m = n2/n1 | Vs = m.a.E donc m = Vs/a.E On se place dans le cas le plus défavorable E = Emin = 16,8 V et a = 40 % donc m = 0,74 On prendra m =0,75 |
|
1.2 |
En utilisant le tableau de sélection de la documentation sur les ferrites, choisir un noyau de type ETD |
Une puissance de 100 W pour une alimentation symétrique correspond à environ 100/1,6 = 62,5 W; on peut choisir un modèle ETD 34 en matériau 3C90 |
|
1.3 |
Calculer le nombre de spires n1 du primaire | Le calcul se fait comme pour une alimentation Forward |
Si on se fixe Bmax = 100 mT, Fmax = Bmax.Ae avec Ae = 97,1 mm²,Fmax = 9,7µWb Emax = 24*1,3 = 31,2 V n1 = [amax.Emax]/[f.Fmax] = 9,9 spires soit n1 = 10 spires
|
1.4 |
Calculer le nombre de spires n2 du secondaire | n2 = m. n1 = 7,4 spires soit 8 donc m = 0,8
Cliquez ici |
|
1.5 |
Calculer l'inductance Lµ d'un des deux enroulements primaires | Pour une noyau ETD34 sans entrefer, l'inductance spécifique est ALo = 2 700 nH donc Lµ = n1².ALo = 270 µH |
|
1.6 |
Calculer les valeurs minimales et maximale de l'intensité i | Is = Ps / Vs = 20 A Imin = Is - Di/2 = 19 A ; Imax = Is +Di/2 = 21 A |
|
1.7 |
Calculer la valeur de l'inductance de filtrage L | L > amax.(1-amax)m.Emax/2.f.Di soit L > 8,6 µH on prendra L = 10µH |
|
1.8 |
Calculer la capacité du condensateur de filtrage C | C > Di/16.f. DVs DVscàc < 10 mV donne C > 125 µF on prendra 150 µF |
|
1.9 |
Calculer les valeurs efficaces de i1, i2 et i |
|
|
1.10 |
Calculer la section des conducteurs des divers bobinages | Primaire : I1 = 7,2 A ; densité de courant 4 A / mm² ; S1 = 1,8 mm² Secondaire : I2 = 12 A ; densité de courant 4 A / mm² ; S2 = 3 mm² Inductance L : I = 20 A ; densité de courant 4 A / mm² ; S1 = 5 mm²
|
|
1.11 |
Le bobinage du transformateur est-il réalisable | S1 = 1,8 mm² , S2 = 3 mm² Section totale St = 2(n1.S1 +n2.S2)= 84 mm² La fenêtre de bobinage du noyau choisi est Sb = 123 mm² Le noyau est trop petit pour porter le bobinage Il faut soit prendre un noyau plis gros soit augmenter la densité de courant à 5 A/mm²
|
|
1.12 |
Choisir un noyau pour réaliser l'inductance | Imax = 21 A; énergie à stocker L.Imax²/2 = 3,3 mJ on choisit le noyau pour LI²= 6,6 mJ en utilisant les graphes LI²(entrefer), on peut par exemple choisir un noyau ETD44 en matériau 3C90 avec un entrefer de 0,8 mm Pour ne pas alourdir l'exercice on garde le même noyau |
|
1.13 |
Calculer le nombre n de spires de la bobine de filtrage |
on calculer AL avec ALo = 3800 nH, µe = 1 800, le = 103 mm , e = 0,8 mm
n = Ö(L/AL) = 5,4 spires soit 6 spires |
|
1.14 |
Calculer l'inductance d'un demi-primaire de n1 spires |
Pour un noyau ETD34 sans entrefer AL = ALo = 2 700 nH L1 = n1²*AL = 270 µH |
|
1.15 |
Quels sont les critères de choix des transistosr K1 et K'1? | Au blocage un transistor doit supporter 2.E , avec E = Emax obtenons une tension de 62,4 V; compte tenu des surtensions dues aux inductances de fuite, il faudra prendre 150 à 200 V en saturation, le transistor conduit le courant maximal m.Imax = 8,4 A; on prendra un courant maximal de 15 à 20 A Compte tenu de la fréquence de découpage et de la tension, on choisira un MOS |
|
1.16 |
Quels sont les critères de choix des diodes D2 et D'2 ? |
è tension inverse maximale 2.m.Emax = 25 V, courant maximal Imax = 21 A on choisit une diode schottky 50 V / 30 à 40 A |
|
1.17 |
Quels sont les critères de choix des diodes D1 et D'1 ? | La tension inverse est 2.Emax = 62,4 V Ces diodes ne conduisent qu'à vide pour permettre la circulation du courant magnétisant; ce courant est celui dans L1 alimentée sous E durant a.T/2 ε = E.a/2.L.f = 0,18 A On choisira donc des diodes rapides 150 V / 0,5 A |
|
2. On utilise l'alimentation ci-dessus dans les conditions suivantes :
|
|||
2.1 |
Calculer le rapport cyclique | a = Vs/ m.E = 26 % |
|
2.2 |
Calculer la valeur de l'ondulation crête à crête de l'intensité i | Di = a.(1-a).m.E2./L.f = 1,54 A
|
|
2.3 |
Calculer la valeur moyenne des courants i, i2 et i1 , en négligeant le courant magnétisant | Si on néglige l'ondulation de Vs, is = Cste = Vs /R = 5 A Le courant moyen dans le condensateur C étant nulle en régime permanent Imoy = Is Imax = Imoy + Di /2 = 5,77 A ; Imin = Imoy -Di /2 = 4,23 A I2moy =(1+ a).Is/2 = 3,15 A I1moy = m.a.Is/2 = 0,52 A
|
|
2.4 |
La démagnétisation est-elle complète ou incomplète ? | a = 26 % < 50 % donc démagnétistion complète |
|
2.5 |
Calculer la valeur maximale du courant magnétisant | ε = a.E/2.f.Lµ = 0,12 A |
|
3. L'alimentation fonctionne à vide, alimentée sous E = 24 V |
|||
La rapport cyclique est réglé à 20 %. |
|||
3.1 |
La démagnétisation est-elle complète ou incomplète ? | a = 20 % < 50 % donc démagnétistion complète |
|
3.2 |
Pour 0 < t < a.T/2, calculer les courants dans tous les interrupteurs | K1 conduit seul durant cette phase; tous les courant sont nuls sauf ik1 = i1 i1 = iµ avec Lµ.diµ/dt = v1 = E soit iµ = E.t/Lµ ce courant évolue de 0 à 90 mA |
|
3.3 |
Pour t > a.T/2, calculer les courants dans tous les interrupteurs | D'1 conduit seule durant cette phase; tous les courant sont nuls sauf i'd1 =- i1 = iµ iµ avec Lµ.diµ/dt = v'1 =-E soit iµ =- E.(t-a.T)/Lµ ce courant évolue de 90 à 0 pour t variant de aT/2 à a.T |
|
La rapport cyclique est réglé à 60 %. |
|||
3.4 |
La démagnétisation est-elle complète ou incomplète ? | a = 60 % > 50 % donc démagnétistion incomplète |
|
3.5 |
Pour 0 < t < a.T/2, calculer les courants dans tous les interrupteurs | K1 est commandé durant cette phase mais iµ(0) < 0 donc c'est D1 qui conduit jusqu'à annulation de iµ : i1 = iµ avec Lµ.diµ/dt = v1 = E soit iµ = E.t/Lµ + iµ(0) D1 se bloque en t1 = -Lµ . iµ(0) /E Ensuite c'est K1 qui conduit et l'évolution de iµ se poursuit avec la même équation En t = a.T/2 : iµ = a.T/2.Lµ + iµ(0) iµ(0)=E.T(1-2.a)/4.Lµ = -40 mA D1 conduit de 0 à 0,5 µs un courant variant de 40 mA à 0 K1 conduit de 0,5 µs à 3 µs un courant variable de 0 à 270 mA |
|
3.6 |
Pour t > a.T/2, calculer les courants dans tous les interrupteurs | K1 est bloqué; iµ est positif donc ne peut circuler dans D1 ;K'1 n'est pascommande donc D'1 conduit seule durant cette phase; tous les courant sont nuls sauf i'd1 =- i1 = iµ iµ=iµ(0)-E(t-a.T)/Lµ ce courant 270 mA à 0 pour t variant de 3 µs à 5,5 µs Cet instant est supérieur à T/2 = 5 µs donc K'1 prend le relais de D'1 le courant i'k1 évolue de 0 à 270 mA pour t variant de 5,5 µs à 8 µs De 8 µs à 10 µs, c'est D1 qui conduit un courant varaint de 270 mA à 40 mA |
|
= 7,2 A
= 11,74 A
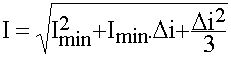= 20,01 A
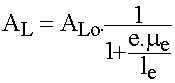= 254 nH