Les alimentations asymétriques de type Flyback ou Forward n'utilisent la caractéristique magnétique du transformateur que dans le premier quadrant (flux et excitation positifs ou nuls). Les alimentations asymétriques travaillent avec un flux alternatif donc utilisent les quadrants 1 et 4 de la caractéristique magnétique. Pour un même circuit magnétique, on peut transmettre de 50 à 70 % de puissance en plus avec un montage symétrique. Elles permettent de réaliser des alimentations de puissances élevées (à partir de quelques centaines de watts) avec des circuits magnétiques de taille réduite.
Les structures sont plus complexes que celles des alimentations asymétriques et nécessitent au moins deux interrupteurs commandés.
Le principe de base et de réaliser une conversion continu - continu indirecte : une structure onduleur convertit la tension continue d'alimentation en tension alternative pour alimenter le transformateur réalisant l'isolement galvanique et l'adaptation de tension; la tension alternative au secondaire du transformateur est redressée puis filtrée pour obtenir la tension de sortie.
On doit avoir au primaire une tension de valeur moyenne strictement nulle pour éviter la saturation du circuit magnétique. Pour cela, on peut placer un condensateur en série avec le transformateur pour éliminer l'éventuelle composante continue ou contrôler celle-ci par la commande.
Plusieurs structures sont possibles suivant le choix de la structure onduleur. Dans ce chapitre, nous limiterons l'étude au montage push-pull.
2 montage push-pull
2.1 Principe
Le montage push-pull est représenté ci-dessous :

Le transformateur possède un bobinage primaire et un bobinage secondaire à point milieu. Les interrupteurs bidirectionnels en courant K1+D1 et K'1+D'1 permettent d'appliquer une tension alternative au primaire. Les deux diodes D2 et D'2 réalisent le redressement double alternance. L'inductance L et le condensateur C réalisent le filtrage de la tension.
2.2 Étude simplifiée en charge
Le fonctionnement du montage push-pull est complexe. Pour aborder simplement l'étude, on va négliger plusieurs paramètres :
Ø le transformateur est supposé parfait : courant magnétisant négligeable, résistances et inductances de fuites négligeables
Ø les interrupteurs, transistors et diodes, sont parfaits
Ø la tension de sortie vs est parfaitement lissée par le filtre L-C
Ø le courant de charge est suffisamment élevé pour que la conduction soit continue dans l'inductance; on a donc toujours au moins une des diodes D2 et D'2 passante.
Le transistor K1 est fermé de 0 à a.T/2 avec a < 1 et le transistor K'1 est fermé de T/2 à (1+a).T/2.
Compte tenu des sens d'enroulements choisis, le transformateur parfait impose en posant m = n2/n1, rapport des nombres de spires d'un demi secondaire à celui d'un demi primaire :
v2 = v'2 = -m.v1 = -m.v'1 et -n1.i1 + n1.i'1 - n2.i2 + n2.i'2 = 0 soit i1 - i'1 = -m.(i2 - i'2).
Ø Première phase : de 0 à a.T/2 la conduction de K1 impose vk1 = 0 donc v1 = v'1 = E , v2 = v'2 = -m.E et v'k1 = 2.E . Les tensions secondaires étant négatives, la diode D2 est bloquée et D'2 conduit.
Nous avons donc i2 = 0 ; i'2 = i et u = -v'2 = m.E.
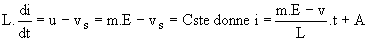 . Comme m.E-Vs > 0 le courant est croissant durant cette phase et A = i(0) = Imin. i'1 et i2 étant nuls, nous avons i'2 = i et i1 = m.i. . Comme m.E-Vs > 0 le courant est croissant durant cette phase et A = i(0) = Imin. i'1 et i2 étant nuls, nous avons i'2 = i et i1 = m.i.
En t = a.T/2, nous avons 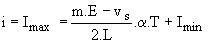
Ø Deuxième phase : de a.T/2 à T/2, K1 et K'1 sont bloqués. Les diodes D1 et D'1 sont bloquées donc i1=i'1=0.
La continuité du courant i dans l'inductance L impose que D2 et/ou D'2 conduisent. Comme la source E ne fournit plus d'énergie, la charge va être alimentée par l'énergie stockée dans L et dans C. Le courant i commence donc à décroître.
Le flux dans le transformateur est positif en t = a.T/2 et ne peut être discontinu. Cela suppose qu'il y ait un courant magnétisant iµ positif. Ce courant ne pouvant plus circuler au primaire, il est transféré au secondaire donc i2 - i'2 = -iµ/m << i ; si D2 conduisait seule, on aurait i2 > 0 et i'2 = 0 ; cela ne satisfait pas l'équation des courants secondaires. Si D'2 conduisait seule, on aurait i2 = 0 et i'2 = iµ/m << i ; ceci ne pemet pas d'assurer la continuité de i.
Il faut donc que D2 et D'2 conduisent simultanément. On a i2 = iµ/m et i'2 = i - iµ/m.
La conduction des deux diodes impose v2 = v'2 = 0 donc v1 = v'1 = 0 , vk1 =v'k1 = E et u = 0 . Les tensions des enroulements étant nulles, le flux est constant durant cette phase ainsi que le courant magnétisant.
Il vient 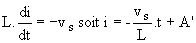 ; le courant i ne pouvant être discontinu, ; le courant i ne pouvant être discontinu, 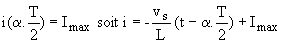 . .
En t = T/2, nous avons 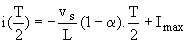
Ø Troisième phase : de T/2 à (1+a).T/2, K'1 conduit donc v'k1 = 0 et v'1 = v1 = - E; le transformateur impose
v2 = v'2 = m.E; la diode D2 conduit et la diode D'2 est bloquée; nous avons u = m.E, i2 = i, i'2 = 0; i1 = 0 et i'1 = m.i.
On retrouve la même tension à l'entrée du filtre donc le courant i évolue comme durant la première phase.
Ø Quatrième phase : de (1+a).T/2 à T, K1 et K'1 sont bloqués; i1 = i'1 = 0 comme dans la phase 2, D2 et D'2 conduisent.
On retrouve le fonctionnement de la deuxième phase avec permutation des rôles des deux diodes .
Les grandeurs des interrupteurs et du transformateur sont de période T donc de fréquence f=1/T; les grandeurs du filtre sont de période T/2 donc de fréquence 2.f. Pour un même choix des composants L et C que dans un alimentation Forward, les ondulations du courant i et de la tension vs sont donc divisées par 2.
La fig.2 donne l'allure des grandeurs.
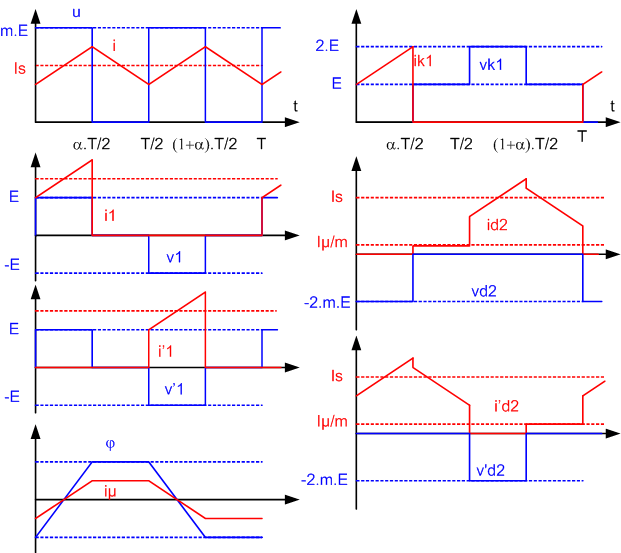
2.3 Calcul des grandeurs
La tension moyenne aux bornes de l'inductance étant nulle, on a Umoy = Vs d'où Vs = m.a.E.
Le rapport cyclique permet donc de régler la tension de sortie.
L'ondulation crête à crête du courant i est 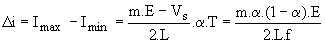 . .
La valeur moyenne du courant dans C étant nulle, nous avons Imoy = (Imax+Imin)/2 = Is.
Nous en déduisons : Imax = Is+Di/2 et Imin = Is-Di/2 .
Le calcul de l'ondulation crête à crête de la tension de sortie est identique à celui du montage Forward avec une fréquence double pour les grandeurs du filtre. D'après le résultat du Chapitre 22, paragraphe 4.7, nous avons : 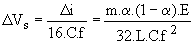 . .
Le graphe de i2(t) étant formé de trois trapèzes, nous avons :
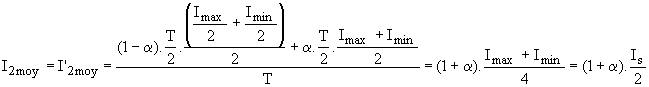 ; ; 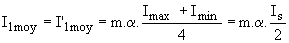 . .
en valeurs efficaces, nous avons : 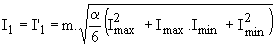 ; ; 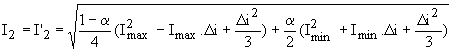 . .
2.4 Courant magnétisant
Soit Lµ l'inductance magnétisante ramenée au primaire et iµ le courant magnétisant.
Dans la première phase v1 = E = Lµ.diµ/dt; on a donc iµ=A+E.t/Lµ. ena.T/2, le courant magnétisant est maximal et vaut Iµmax = A+a.E/2.Lµ.f.
Durant la deuxième phase v1=v'1=0 donc iµ = Cste = Iµmax.
La tension primaire étant alternative, on obtient des valeurs opposées du courant durant la troisième et la quatrième phase.
Le courant magnétisant étant alternatif iµ(0)= -iµ (T/2); on en déduit A = a.E/4.Lµ.f.
La fig.3 donne l'allure du courant magnétisant : 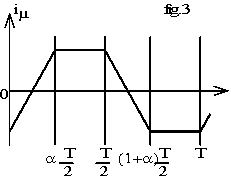
En charge ce courant est négligeable devant les courants calculés au 2.2.
2.5 Fonctionnement à vide
Lorsque le courant de charge est nul, on ne peut négliger le courant magnétisant du transformateur. L'équation aux ampères-tours est n1.i1-n1.i'1+n2.i2-n2.i'2 = n1.iµ. Le courant i étant nul, les diodes D2 et D'2 ne peuvent conduire et les courants secondaires sont nuls. On en déduit iµ = i1-i'1.
De 0 à a.T/2, K1 conduit donc vk1 = 0 imposant v1 = v'1 = E et v'k1 = 2.E; les diodes D1 et D'1 sont bloquées: i'1 = 0 et i1 = iµ. L'équation Lµ.diµ/dt = E montre que le courant magnétisant croît. En a.T/2, le courant magnétisant est égal à Iµ1 > 0.
En a.T/2+, K1 et K'1 sont bloqués; i1-i'1 = Iµ1 > 0; si D1 conduisait, on aurait v1 = E et v'k1=2.E donc D'1 serait bloquée et l'on aurait i1= -id1 = Iµ1 > 0. D1 ne pouvant être traversée par un courant inverse, D1 ne peut pas conduire. Il faut donc que D'1 conduise pour assurer la continuité du courant magnétisant;
on a i'd1 = -i'1= iµ > 0. v'k1 = 0 donc v1=v'1 = - E. Lµ.diµ/dt = - E donc le courant magnétisant décroît avec une pente opposée à celle de la phase de croissance.
A chaque demie période, un demi-primaire magnétise le transformateur et l'autre demi-primaire le démagnétise.
On doit distinguer deux cas suivant la valeur du rapport cyclique :
v Si a < 50 %, la phase de magnétisation donc celle de démagnétisation dure moins d'un quart de période; le courant magnétisant s'annule avant T/2; on fonctionne en démagnétisation complète.
v Si a < 50 %, la démagnétisation ne peut plus être complète.
démagnétisation complète
Ø Première phase : de 0 à a.T/2, K1 conduit et Lµ.diµ/dt = E; le courant magnétisant étant initialement nul, nous avons iµ = E.t/Lµ. ena.T/2, iµ = Iµ1 = E. a.T/2.Lµ.
Ø Deuxième phase : pour t > a.T/2, D'1 conduit et Lµ.diµ/dt = -E. 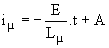 ; avec iµ( a.T/2)=Iµ1, il vient ; avec iµ( a.T/2)=Iµ1, il vient 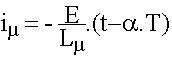 . La diode D'1 se bloque en t = a.T < T/2. . La diode D'1 se bloque en t = a.T < T/2.
Ø Troisième phase : de a.T à T/2, tous les interrupteurs sont ouverts et tous les courants sont nuls.
A la demie période suivante, le fonctionnement est semblable; durant la conduction de K'1, le courant magnétisant varie de 0 à -Iµ1; ensuite D1 assure la démagnétisation.
La fig.4 donne l'allure des grandeurs : 
démagnétisation incomplète
Ø Première phase : en 0+ K1 conduit et le courant magnétisant est négatif. vk1 = 0 impose v1 = E et v'k1 = 2.E; la diode D'1 est bloquée. La diode D1 conduit pour assurer la continuité de iµ : 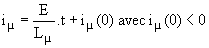 . Le courant magnétisant s'annule en t1 = -Lµ.iµ(0)/E; la diode D1 se bloque . Le courant magnétisant s'annule en t1 = -Lµ.iµ(0)/E; la diode D1 se bloque
Ø Deuxième phase : pour t > t1, K1 conduit et Lµ.diµ/dt = E; 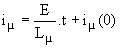 . .
Ø Troisième phase : comme dans le cas de la démagnétisation complète, la diode D'1 conduit pour assurer la continuité de iµ. Lµ.diµ/dt = -E donc Iµ = B-E.t/Lµ;
La continuité du courant en a.T/2 impose B=Iµmax+E.aT/2.Lµ = iµ (0)+E. a.T/Lµ.
On en déduit iµ=iµ(0)-E(t-a.T)/Lµ
La diode D'1 conduit tant que le courant est positif. Le courant iµ étant alternatif, il s'annule en t1+T/2.
Nous en déduisons iµ(0)=E(t1+T/2+-a.T)/Lµ . en remplaçant t1 par sa valeur, il vient : iµ(0)=E.T(1-2.a)/4.Lµ .
Ø Quatrième phase : lorsque D'1 se bloque, K'1 est commandé à la fermeture depuis T/2 et donc conduit jusqu'à (1+a).T/2.

Le fonctionnement à vide ou à faible charge nécessite au primaire des interrupteurs réversibles en courant pour assurer la démagnétisation.
|


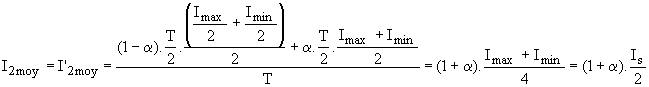 ;
; 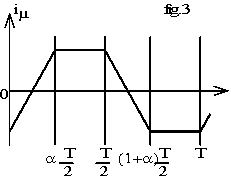
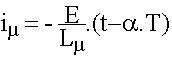 . La diode D'1 se bloque en t =
. La diode D'1 se bloque en t = 
