Électronique de puissance
xxxxxxModule 4 : xxxxxxx "Alimentations continues " |
Chapitre 4.3
Alimentation Flyback |
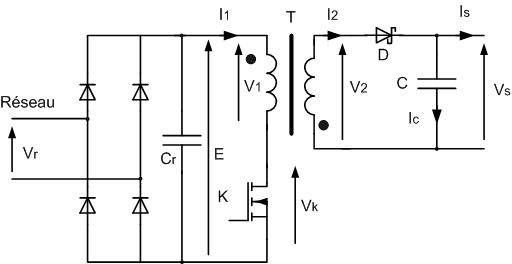
On étudie une alimentation de type Flyback réalisée suivant le schéma ci-dessous :
on donne : è la tension du réseau : Vr = 230 V ± 20 % è la tension de sortie : Vs = 12 V ; ondulation DVscàc £ 50 mV è la puissance de sortie : Ps £ 40 W è fréquence de découpage : f = 100 kHz è le rendement estimé: h = 75 % è la valeur maximale du rapport cyclique : a = 45 % è les critères de choix des ferrites et les caractéristiques de noyaux : cliquez ici pour ouvrir ce fichier (format pdf)
|
|||
1. Dimensionnement |
|||
1.1 |
Doit-on choisir le mode de démagnétisation complète ou incomplète | La puissance étant inférieure à 50 W, on choisit la démagnétisation complète |
|
1.2 |
Quelle est la plage de variation de la tension crête du réseau ? |
La tension crête est Vrmax = Ö2. Vr 184 < Vr < 276 V donc 260 < Vrmax < 391 V |
|
1.3 |
Si on suppose une chute de tension maximale de 1 V dans une diode du redresseur et une ondulation résiduelle de 10 V après filtrage par Cr, quelle est la plage de variation de la tension E ? | Emin = Vrmax - 2*Vd - DV dans le cas le plus défavorable Vrmax = 260 V, Vd = 1 V et DV = 10 V donc Emin = 248 V Emax = Vrmax dans le cas le plus défavorable Emax = 391 V |
|
1.4 |
Calculer la valeur de l'inductance primaire | Puissance en entrée Pe = Ps/h = 53,3 W
|
|
1.5 |
En utilisant le tableau de sélection de la documentation sur les ferrites, choisir un noyau de type ETD | Pour une puissance de 40 W, on peut choisir un noyau ETD29 A la fréquence de 100 kHz, on peut prendre le matériau 3C90 |
|
1.6 |
Choisir une induction maximale et calculer le flux maximal | Utiliser les données constructeur Valeur préconisée Bmax = 100 mT ; on a alors Fmax = Bmax.Ae = 7,6µWb |
|
1.7 |
calculer le nombre de spires au primaire | L'intensité maximale au primaire est Î1 = Emax.amax/f.L1 soit Î1 = 1,5 A n1 = Emin.amax /f.Fmax = 147 spires |
|
1.8 |
calculer le nombre de spires au secondaire | n2 = n1.(1-amax).(vs +Vd)/[amax.Emax] en prenant une chute de tension Vd = 0,8 V dans la diode n2 = 6 spires |
|
1.9 |
calculer l'épaisseur e de l'entrefer nécessaire | utilisez les graphes LI²(e) de la documentation |
AL = 220 nH ; Î1 = 1,5 A donc LI² = 2,6 mJ Les graphes donnent pour le noyau ETD 29 ; e = 0,7 mm cet entrefer est réalisable |
1.10 |
calculer les valeurs maximales et minimales des courants primaire et secondaire | Au primaire I1max = 1,5 A et I1min = 0 (démagnétisation complète) au secondaire I2max = n1.I1max/n2 = 36,2 A et I2min = 0 |
|
1.11 |
calculer les valeurs efficaces des courants primaire et secondaire | utilisez la formule : |
au primaire Dt = a.T donc I = Î1.Ö(a/3) = 0,58 A au secondaire Dt = (b-a).T = b'.T
donc I2 = Î2.Ö(b'/3) = 16,1 A
|
1.12 |
calculer le diamètre des fils cylindriques à utiliser au primaire et au secondaire | Section = Ieff / densité de courant = p.D² /4 en prenant une densité de 4 A/mm²: au primaire S1 = 0,15 mm² soit un diamètre D1 = 0,43 mm on prendra 0,45 mm au secondaire S2 = 4 mm² soit un diamètre D2 = 2,3 mm on prendra 2.5 mm
|
|
1.13 |
L'effet de peau doit-il être pris en compte ? | Épaisseur de peau d = 70/Öf = 7 mm Le diamètre des fils étant inférieur à 2.d l'effet de peau ne modifie pas la section utile des conducteurs |
|
1.14 |
calculer la surface occupée par les bobinages en majorant les sections de 10 % pour tenir compte de l'isolant |
S1 = 0,17 mm² et S2 = 5,4 mm² Section totale St = n1.S1 +n2.S2 = 58,1 mm² |
|
1.15 |
Le bobinage est-il réalisable ? |
St = 58,1 mm² ; la notice du noyau choisi donne une fenêtre de bobinage Sb = 95 mm² = 1,64.St ; le bobinage ne contiendra pas dans la fenêtre Il faut recommencer les calculs à la question 1.5 avec un noyau plus gros |
|
1.16 |
Montrer qu'un noyau ETD34 convient | Reprise du calcul : Bmax = 100 mT ; on a alors Fmax = Bmax.Ae = 9,7 µWb n1 = Emin.amax /f.Fmax = 115 spires n2 = n1.(1-amax).(vs +Vd)/[amax.Emax] = 5 spires Les graphes donnent pour le noyau ETD 29 ; e = 0,6 mm cet entrefer est réalisable Section totale St = n1.S1 +n2.S2 = 47,2 mm² Sb = 123 mm² = 2,6.St ; le bobinage est possible |
|
1.17 |
calculer les résistances des bobinages et les pertes par effet Joule |
R = r.L/S La notice du noyau donne une longueur moyenne par spire de 53 mm Primaire : longueur 60*115 = 6 900 mm = 6,9 m ; section 0,17 mm² ; résistance 0,65 W ; pertes Joule R1.I1eff² = 0,22 W Secondaire : longueur 60*5 = 300 mm = 0,3 m ; section 5,4 mm² ; résistance 0,9 mW ; pertes Joule R2.I2eff² = 0,21 W |
|
1.18 |
Évaluer le rendement | Pertes par effet Joule : 0,43 W Pertes magnétiques : 1 W ( données constructeur) Pertes dans le transistor évaluées à 5 W Pertes dans le diode : courant moyen Id égal au courant de charge donc 40/12 = 3,3 A ; pertes Vd.Id = 2,7 W soit environ 3 W Les pertes totales sont estimées à 9,5 W rendement = Ps /(Ps + p) = 81 % donc supérieur à la valeur fixée |
|
1.19 |
calculer la capacité du condensateur C | C = (1-a).T.Is/ DVscàc DVscàc < 50 mv donne C > 367 µF on prendra 470 µF |
|
1.20 |
Quels sont les critères de choix du transistor K | au blocage le transistor doit supporter E + vs/m , avec E = Emax et m = 0,04 nous obtenons une tension de 667 V; compte tenu des surtensions dues aux inductances de fuite, il faudra prendre 800 à 1 000 V en saturation, le transistor conduit le courant maximal 1,47 A; on prendra un courant maximal de 3 à 5 A Compte tenu de la fréquence de découpage, on choisira un MOS ou un IGBT |
|
1.21 |
quels sont les critères de choix de la diode | au blocage la diode doit supporter m.E + vs , avec E = Emax et m = 0,04 nous obtenons une tension de 29 V; compte tenu des surtensions dues aux inductances de fuite, il faudra prendre 50 à 60 V en saturation, la diode conduit le courant maximal 34 A; on prendra un courant maximal de 40 à 50 A Pour minimiser les pertes on choisira une diode schottky |
|
on utilise l'alimentation ci-dessus dans les conditions suivantes :
|
|||
2.1 |
calculer la tension de sortie | vs = a.E.Ö(Rs/2.L1.f) = 14,2 V |
|
2.2 |
calculer la valeur maximale du courant i1 | Î1 = a.E /L1.f = 0,75 A |
|
2.3 |
calculer la durée de conduction de la diode D |
|
|
2.4 |
La démagnétisation est-elle complète ? | K conduit pendant a.T = 3 µs et la diode durant b'.T = 2,75 µs elle se bloque donc en t = 5,75 µs soit avant T = 10 µs La démagnétisation est complète |
|
2.5 |
L'inductance de fuites totale ramenée au primaire est Lf = 50 µH; calculer la surtension à la coupure aux bornes de K pour un temps de commutation de 100 ns. | La formule à utiliser est : Lf.Î1/tf = 375 V |
|
2.6 |
quelle est la valeur de la capacité C' à brancher aux bornes de K pour limiter la surtension à 100 V ? | Avec C' la valeur de la surtension est Î1.Ö(Lf/C'); il faut prendre C' = 2,8 nF ; on prendra 3,3 nF |
|