On étudie une alimentation de type Bust réalisée suivant le schéma ci-dessous :
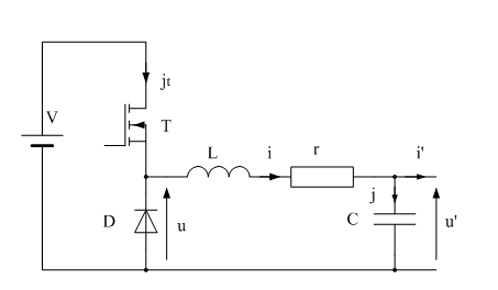
On donne V = 300 V :
è la tension d'entrée : V = 24 V ± 10 %
è la tension de sortie : valeur moyenne U' = 5 V ; ondulation DU'càc £ 50 mV
è l'intensité de sortie : 1 A £ I' £ 3 A
è fréquence de découpage : f = 100 kHz |
1. Dimensionnement
On utilise le calcul simplifié en conduction permanente; on néglige la résistance r de la bobine.
|
1.1 |
Compte tenu de la variation de la tension d'entrée, calculer les limitées du rapport cyclique |
U' = U = a. V
V = 24*0,9 = 21,6 V donne a = 23,1 %
V = 24*1,1 = 26,4 V donne a = 18,9 %
Cliquez ici |
1.2 |
Quelle condition doit remplir l'ondulation du courant i pour que la conduction soit permanente pour tout régime ? |
L'intensité i étant de forme triangulaire Imin = I -Di/2
La valeur moyenne I de i est égale à celle de i' car Jmoy = 0
On sera en conduction permanente si Imin > 0 donc Di < 2.I
Cliquez ici |
1.3 |
Quelle est l'expression de l'ondulation du courant i ? En déduire la valeur minimale de L |
Di = a.(1-a).V/L.f ; Di < 2.I donne la valeur minimale de L en se plaçant dans le cas le plus défavorable soit I = 1 A et V = 26,4 V
L > a.(1-a).V/ 2.I.f soit L > 20,3 µH
On prendra L = 25 µH qui donnera Di = 1,62 A dans le cas le plus défavorable
Cliquez ici |
1.4 |
Quelle est l'expression de l'ondulation de la tension de sortie ? En déduire la valeur de C. |
Du' = a.(1-a).V/L.C.f ² ; dans le cas le plus défavorable soit V = 26,4 V, Du' < 50 mV donne C > 40,5 µF
On prendra C = 47 µF on aura donc Du' = 43 mV dans le cas le plus défavorable
Cliquez ici |
1.5 |
Quels sont les critères de choix du transistor MOS T ? Quel choix faites vous dans la liste proposée en cliquant ici |
A l'état bloqué, le transistor supporte la tension V soit 26,4 V dans le cas le plus défavorable
A l'état passant, le courant maximal dans T est I + Di/2 = 3,81 A dans le cas le plus défavorable
En prenant une marge de sécurité, il faut choisir un transistor MOS 50V / 5A
Dans la liste proposée c'est le type URF014 qui convient le mieux
Cliquez ici |
1.6 |
Quels sont les critères de choix de la diode D? Quel choix faites vous dans la liste proposée en cliquant ici |
A l'état bloqué, la diode supporte la tension V soit 26,4 V dans le cas le plus défavorable
A l'état passant, le courant maximal dans D est I + Di/2 = 3,81 A dans le cas le plus défavorable
En prenant une marge de sécurité, il faut choisir une diode 50V / 5A
Dans la liste proposée il vaut mieux choisir une diode schottky qui a une plus faible chute de tension donc qui introduira moins de pertes. Le type SB540 convient
Cliquez ici |
2. Etude en conduction permanente
On veut étudier le fonctionnement par la méthode harmonique.
La tension d'entrée est V = 24 V ; le rapport cyclique est réglé à 22 % et la charge est une résistance R = 2,2 W . La résistance de la bobine est r = 50 mW.
On néglige les chutes de tension dans T et D.
|
2.1 |
Calculer la décomposition en série de Fourier de la tension u(t) |
Aide |
u est un créneau 0 - 24V de fréquence f et de rapport cyclique a = 5/24 = 20,8 % donc
u = a.V + S (2.V/p.n).cos(n.w.t - p.n.a)
Cliquez ici |
2.2 |
En déduire les valeurs moyennes de i et u' |
Pour la composante continue Umoy = a.V, L est un court-circuit et C un circuit ouvert; on a donc :
Imoy = Umoy /(R+r) = 2,35 A et U'moy = R.moy = 5,16 V
Cliquez ici |
2.3 |
Donner les expressions des hramoniques de rang n de i et u' |
|
2.4 |
Calculer les amplitudes des harmoniques de u, i et i' jusqu'au rang 5 |
|
2.5 |
Peut-on utiliser la méthode du premier harmonique pour simplifier le calcul de i et u' ? |
La méthode du premier harmonique consiste à remplacer la série de Fourier par la somme du terme continu et du premier harmonique non nul. Cela suppose que les harmoniques suivant soient négligeables devant ce premier harmonique.
Cela n'est pas pas très juste pour i car I3 = I1/2,6; ce peut être justifié pour u' car U3 = U1 / 5,2
Cliquez ici |
2.6 |
Calculer la valeur efficace du courant i |
I = racine[Io²+(Î1²+Î2²+Î3²+Î4²+Î5²)/2] = 2,39 A
Cliquez ici |
3. Etude simplifiée en conduction discontinue
La tension d'entrée est V = 24 V ; le rapport cyclique est réglé à 22 % et la charge est une résistance R = 50 W
|
3.1 |
Montrer que la conduction est discontinue |
Si on est en conduction continue, on a U = a.V = 5,28 V
I = U / (R+r) = 0,11 A ; Di = a.(1-a).V/L.f = 1,65 A
Imin = I - Di/2 = -0,72 A < 0 donc la conduction ne peut être continue
Cliquez ici |
3.2 |
En négligeant l'ondulation de u' et r , calculer la valeur moyenne U' de la tension de sortie |
Cette valeur est donnée par 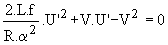
On obtient U' = 11,87 V
Cliquez ici |
3.3 |
Calculer les valeurs moyenne et maximale de l'intensité i |
I = I' = U' /R = 0,24 A
Imax = a.(V-U')/L.f = 1,07 A
Cliquez ici |
3.4 |
Calculer la durée de conduction de la diode D |
D conduit de a.T à b.T avec b = 2.I/Imax = 44,5 %
Le temps de conduction de D est donc (b - a) / f = 2,25 µs
Cliquez ici |
4. Pertes et rendement
On suppose que V = 24 V, a = 22 % et I'= 3 A
Pour simplifier l'étude, on néglige l'ondulation de i et de u'
|
4.1 |
Calculer la puissance fournie à la charge |
U = a.V = 5,28 V ; I = I' = 3 A ;
U' = U -r.I = 5,13 V ; Ps = U'.I = 15,4 W
Cliquez ici |
Etude des pertes dans le transistor
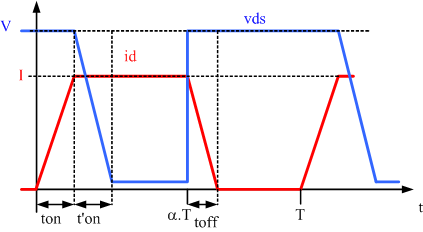
On donne : ton = 50 ns ; t'on = 20 ns ; toff = 40 ns
|
4.2 |
Calculer l'énergie perdue durant la fermeture de T, en négligeant la tension de saturation |
Ecrire les expressions de id(t) et vds(t) sur ton puis intégrer
dw = id.vds.dt sur le temps de fermeture
Faire de même entre t' t - ton = 0 et t' = t'on
Aide |
|
4.3 |
Calculer l'énergie perdue durant la conduction de T, sachant que la résistance du MOS saturé est Rdson = 0,2 W
|
La puissance perdue est Rdson.I² donc l'énergie est :
Wtcon = Rdson.I².(a.T -ton - t'on) = 3,8 µJ
Cliquez ici |
4.4 |
Calculer l'énergie perdue durant l'ouverture de T, en négligeant la tension de saturation |
|
4.5 |
Calculer la puissance dissipée dans le transistor |
Energie totale perdue : Wt = Wton + Wtcon + Wtoff = 7,76 µJ
Cette énergie est dissipé en une période donc Pt = Wt / T = Wt . f = 776 mW
Cliquez ici |
Etude des pertes dans la diode D
Durant la conduction de la diode, la tension directe à ses bornes est VF = 0,55 V
|
4.6 |
Déduire des formes d'onde du transistor T, les graphes de la tension vd aux bornes de la diode et de l'intensité jd dans la diode |
|
4.7 |
Calculer l'énergie perdue durant les commutations de la diode |
|
4.8 |
Calculer l'énergie perdue durant la conduction de la diode |
La diode conduit pendant tdcon = (1 - a).T - toff = 7,79 µs
L'énergie dissipée est Wdcon = VF.I.tdcon = 8,6 µJ
Cliquez ici |
4.9 |
Calculer la puissance dissipée dans la diode |
Energie totale perdue : Wt = Wdton + Wdcon + Wdoff = 8,72 µJ
Cette énergie est dissipé en une période donc Pd = Wd / T = Wdt . f = 872 mW
Cliquez ici |
Pertes et rendement |
4.10 |
Calculer la puissance perdue dans la résistance r de la bobine |
|
4.11 |
Calculer les pertes totales et le rendement du montage |
pertes p = Pt + Pd + PL = 2,1 W
rendement h = Ps / Ps +p = 88 %
Cliquez ici |
On étudie une alimentation élevant la tension ; on donne :
è la tension d'entrée Ve = 5 V
è la tension de sortie Vs = 12 V
è l'ondulation maximale de la tension de sortie DVs = 0,1 V
è l'intensité maximale en sortie Is varie de 2 à 5 A
è la fréquence de découpage f = 400 kHz
On utilisera un ciruit intégré LM 3478 dont la documentation est disponible en cliquant
ici |
1 Calcul des composants du montage
On utilise le montage de base de la documentation repris ci-dessous
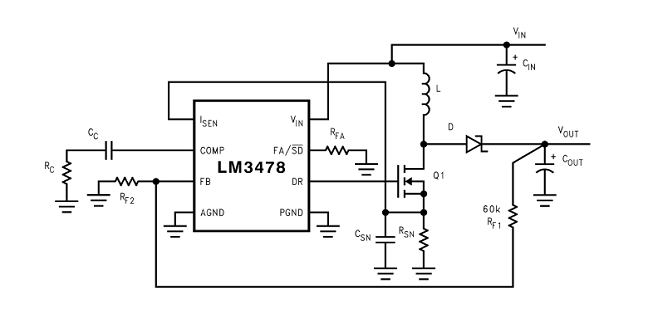
|
1.1 |
En utilisant les formules de la page 13, calculer la valeur du rapport cyclique; on prendra une chute de tension de 1 V dans le MOS et de 0,7 V dans la diode |
La formule à utiliser est : Vout + VD = (VIN - VQ)/(1-D)
1 - D = (5 - 1) / (12 + 0,7) = 0,315
Le rapport cyclique est donc a = D = 68,5 %
Cliquez ici |
1.2 |
En utilisant les formules de la page 15, calculer la valeur de l'inductance L |
La formule à utiliser est : L > D.(1-D).VIN / 2.Iout .fs
Dans la cas le plus défavorable Is = 2 A donc L > 0,67 µH
Si nous voulons, comme préconisé, une ondulation de l'ordre de 30 % du courant de sortie, nous aurons 0,3.D.VIN/L.f = 2 A soit L = 1,3 µH; nous prendrons 1,5 µH
Cliquez ici |
1.3 |
Calculer la valeur de la résistance RF2 |
La formule à utiliser est : Vout = 1,26*(1+RF1/RF2)
Avec RF1 = 60 kW, il vient RF2 = 7 kW
Cliquez ici |
1.4 |
Calculer la valeur de la résistance RSN = RSEN |
La formule à utiliser est : 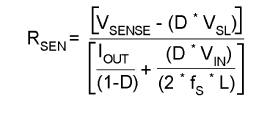
La documentation donne VSENSE = 0,165 V (page 3) et VSL = 0,092 V (page 4)
Pour Is = Iout = 5 A ; RSEN = 5,4 mW
Cliquez ici |
1.5 |
Calculer la valeur maximale de l'intensité dans l'inductance L |
La formule à utiliser est : 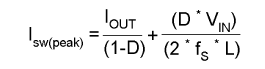
Pour Is = Iout = 5 A ; Iswp = 18,7 A
Cliquez ici |
1.6 |
Quels sont les critères de choix de la diode D ? |
Le courant maximal est celui de l'inductance soit 19 A
Au blocage, la tension inverse maximale est égale à Vout soit 12 V
Il faut choisir une diode schottky 30 A / 25 V
Cliquez ici |
1.7 |
Quels sont les critères de choix du transistor Q1 ? |
Le courant maximal est celui de l'inductance soit 19 A
Au blocage, la tension inverse maximale est égale à Vout soit 12 V
Il faut choisir un MOS 30 A / 25 V
Cliquez ici |
1.8 |
Quels sont les critères de choix du condensateur d'entrée CIN ? |
Sa valeur doit être de 100 à 220 µF par exemple 150 µF
Ce condensateur doit supporter un courant efficace donné par la formule de la page 17 : Icin = 0,28 A
Cliquez ici |
1.9 |
Quels sont les critères de choix du condensateur d'entrée COUT ? |
Dans le cours, on a donné l'expression simplifiée de l'ondulation de sortie :
Du = a.E/[(1-a).R.C.f]
Avec Du = 0,1 V , a = 68,5 %, E = Vin = 5 V, R = Vs / Is = 2,4 W, il vient
C = 113 µF ; on prendra 120 µF
Le courant efficace dans ce condensateur, calculé à partir de la formule de la page 17 est : Icout = 7,5 A
Cliquez ici |
2 Etude d'un point de fonctionnement
La tension de sortie étant Vs = 12 V, la charge est une résistance R = 4 ohms.
|
2.1 |
Peut-on utiliser la méthode simplifiée ? |
La constante de temps de la bobine est L/r = 150 µs = 40. T, T étant la période de découpage
La constante de temps en sortie R.C = 480 µs = 192.T
Les constantes de temps étant très grandes devant la période, on peut utiliser la méthode simplifiée
Cliquez ici |
2.2 |
Si on tient compte de la résistance r = 10 mW de l'inductance, quelle est la valeur du rapport cyclique ? |
Nous avons alors 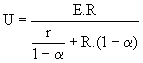 avec U = Vout et E = Vin avec U = Vout et E = Vin
Nous en déduisons : U.R.a² -R.(2.U-E).a +U.(r+R)-E.R = 0 soit 48.a²-76.a+28,1 =0
On a deux solutions : 99,4 % et 59,4 % ; la valeur qui convient est manifestement a = 59,4 %
Cliquez ici |
2.3 |
Calculer la valeur moyenne et l'ondulation crête à crête du courant dans l'inductance en négligeant r |
Si on néglige les pertes , E.J = U.Is donc J = U.Is/E = 7,2 A
Dj = a.E / f.L = 4,9 A
Cliquez ici |