Électronique de puissance
xxxxxxModule 3 : xxxxxxx "Conversion DC - DC " |
Chapitre 3.3
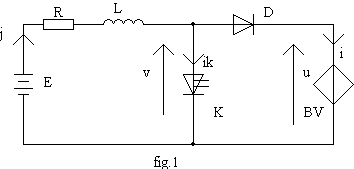
Hacheur parallèle |
1 |
Peut-on utiliser la méthode simplifiée ? | La constante de la charge est t = L/R = 3 ms La période de découpage est T = 1 / f = 1 ms t = 3.T donc on ne peut pas utiliser la méthode simplifiée |
2 |
Calculer la valeur limite de a permettant la conduction permanente dans la charge | On doit avoir X.Y = exp(-a.T/t) . exp[-(1-a).T/t] = exp(-T/t) = 0,717 soit a > 78,9 % |
Le rapport cyclique est réglé à a = 85 % |
||
3 |
Calculer les valeurs moyennes de v, j et i | a > 41 % donc la conduction permanente est permanente V = (1- a).U = 7,2 V La tension moyenne aux bornes de L étant nulle, J = (E - V) / R = 9,6 A
X = exp[-a.T/t]= 0,753. Y = exp[-(1-a).T/t]= 0,951 Jmax = E/R - U.X.(1-Y)/R.(1-X.Y) =11,6 A ; I = 1,43 A |
4 |
Calculer les valeurs maximale et minimale de i | Imin = Jmin =E/R -U.(1-Y)/R.(1-X.Y) = 7,48 A
Cliquez iciImax = Jmax = 11,6 A |
Le rapport cyclique est réglé à a = 30 % |
||
5 |
Calculer la durée de conduction de la diode D | La conduction est discontinue
X = 0,905 , Jmax = 2,28 A , b = 39,4 % D conduit de a.T à b.T soit durant 93,6µs |
6 |
Calculer les valeurs moyennes de u et j | V = (b-a).U + (1-b).E = 11,77 V ; J = (E - V) /R = 455 mA |
1 |
Montrer que l'on peut utiliser la méthode simplifiée | La constante de la charge est t = L/R = 3 ms La période de découpage est T = 1 / f = 0,1 ms t >>T donc on peut utiliser la méthode simplifiée |
2 |
Déterminer la valeur minimale de a permettant la conduction continue | On doit avoir soit 1,6. a² + 94,4.a - 72 = 0 Les racines de cette équation sont -5 975% et 75,3 % Il faut donc a > 75,3 % |
3 |
Pour a = 85 % calculer les valeurs moyennes de v, j et i et l'ondulation crête à crête de j | On est en conduction permanente donc V = (1 - a).U = 7,2 V J = (E - V) / R = 9,6 A Conservation de la puissance : E.J = U.I soit I = 2,4 A Dj = a.(1-a).U / L.f = 408 mA |
4 |
Pour a = 30 % calculer les valeurs moyennes de v, j et i | On est en régime de conduction interrompue Jmax = j(a.T) = a.E.T / L = 240 mA b = a + (t /T).R.Jmax/( R.Jmax-E+U) = 40 % J = b. Jmax /2 = 48 mA ; V = E - R.J = 11,98 V E.J = U.I donc I = 12 mA
|
1 |
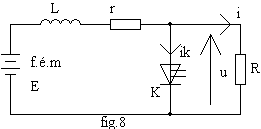
Avec un rapport cyclique a = 0, le courant moyen dans la f.é.m. E est J = 20 A, calculer R | Si a = 0, on a un circuit E - R+r - L en régime permanent continu I = J = E / (R + r) d'où R = 14,2 W |
Le rapport cyclique est réglé à a = 50 % et la fréquence de découpage est f = 10 kHz |
||
2 |
Calculer l'ondulation crête à crête du courant j dans E |
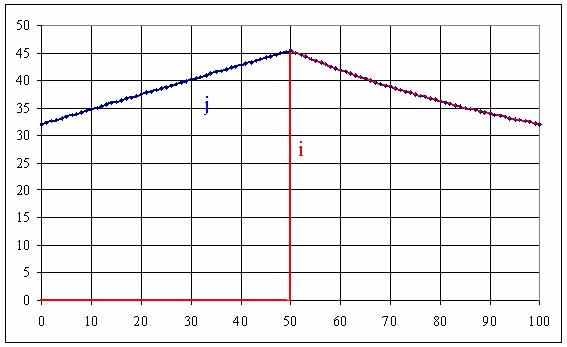
avec t =L/r = 1,25 ms, T =1/f = 0,1 ms, X = exp(-a.T/t) = 0,961 R' = R+r, t' =L/R' = 66,7 µs , Y = exp([-(1-a).T/t'] = 0,473 Jmin = 32 A ; Jmax = 32 A ; 45,4 A ; Dj = 13,4 A
|
3 |
Calculer la valeur moyenne du courant i ; en déduire la valeur moyenne de u. |
I = 18,9 A ; U = R.I = 280 V |
4 |
Calculer la valeur moyenne du courant j et la valeur de la résistance Rh qui branchée directement aux bornes de E produirait la même intensité |
E = r.j + L.dj/dt+u la tension moyenne aux bornes de l'inductance étant nulle, J = (E-U)/r = 24,9 A Rh = E / J = 12 W |
5 |
Comparer Rh à R et conclure | Rh / R = 0,81 Si on négligeait r, on aurait Rh = R.(1 - a) soit Rh / R = 0,5 La résistance de la bobine n'est pas négigeable dans les conditions d'emploi du montage |
6 |
Tracer les graphes de i et j |
|
Le rapport cyclique est réglé à a = 30 % et on néglige la résistance r de la bobine |
||
7 |
Quelle est la fréquence minimale de découpage qui permet de faire cette hypothèse ? | Il faut que les deux constantes de temps t =L/r = 1,25 ms et t' =L/R' = 66,7 µs , soient trés grandes devant la période : il faut donc t' >> T = 1 / f soit f >> 1 /t' = 15 kHz On doit donc avoir f > 150 kHz |
8 |
La fréquence de découpage est réglée à f = 200 kHz; calculer la valeur moyenne du courant j | En négligeant r, le montage est équivalent à une résistance Rh = R.(1-a) = 10,36 W ; J = E / Rh = 29 A |