Électronique de puissance
xxxxxxModule 3 : xxxxxxx "Conversion DC - DC " |
Chapitre 3.3
Hacheur parallèle |
On étudie la structure Boost ci-contre : 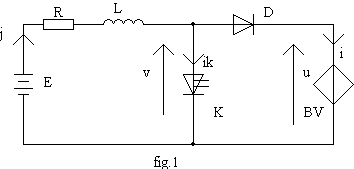
Ø De 0 à a.T , K est fermé imposant v = 0; D est bloquée et impose i = 0; durant cette phase on accumule de l'énergie dans l'inductance. L'intensité j augmente et tend vers la valeur E/R.
Ø De a.T à T, K est ouvert; l'intensité j décroît et tend vers la valeur (E-U) /R; la structure étant élévatrice de tension, U > E donc cette limite est négative; D interdisant la circulation d'un courant i < 0, nous aurons donc deux types de fonctionnement :
v l'énergie accumulée dans L durant la première phase est suffisante pour maintenir j > 0 durant la deuxième phase; la conduction dans la source est ininterrompue et j > 0 pour toute valeur du temps.v l'énergie accumulée dans L ne permet plus la conduction permanente; les courants i et j s'annulent au temps b.T avec a < b < 1. La conduction est alors interrompue.
1.2 Étude en conduction permanente
Étudions le régime permanent pour lequel toutes les grandeurs sont périodiques de fréquence f = 1 / T.
Ø De 0 à a.T, nous avons v = E-R.j-L.dj/dt = 0 soit j + t.dj/dt = E/R en posant t = L/R.
Nous en déduisons j = A.exp(-t/t) + E/R ; le courant j est minimal en t =0d'où Jmin = A + E/R et
j = (Jmin - E/R).exp(-t/t) + E/R . A la fin de cette phase, le courant source est maximal ;
posons X = exp(-a.T/t); il vient : j(a.T) = Jmax = X.Jmin - (1-X).E/R (Eq.1)
Ø De a.T à T, la conduction de D impose v = U = E-R.j-L.dj/dt soit j + t.dj/dt = (EU)/R.
En posant t' = t -a.T, nous obtenons ![]() ; avec j(t'=0)=Jmax, il vient :
; avec j(t'=0)=Jmax, il vient :
![]() ; en t = T soit t' =(1-a).T, le courant devenu périodique reprend sa valeur minimale initiale;
; en t = T soit t' =(1-a).T, le courant devenu périodique reprend sa valeur minimale initiale;
en posant ![]()
Les équations (Eq.1) et (Eq.2) permettent d'exprimer les extremums de j :
![]() .
.
L'ondulation crête à crête est : ![]() (Eq.5); notons que X.Y = exp(-T/t) ne dépend pas du rapport cyclique et que l'ondulation est indépendante de la f.é.m E.
(Eq.5); notons que X.Y = exp(-T/t) ne dépend pas du rapport cyclique et que l'ondulation est indépendante de la f.é.m E.
La fig.2 donne l'allure des graphes : 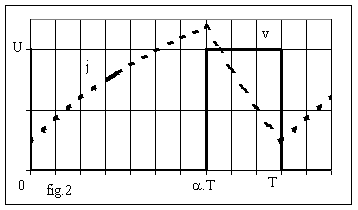
La valeur moyenne de la tension v est V = (1-a).U; on a v = E-R.j-L.dj/dt; la tension moyenne aux bornes d'une inductance pure est nulle en régime périodique donc V = E - R.J en valeurs moyennes
soit J = [E-(1-a).U]/R.
Calculons la valeur moyenne du courant i dans la charge : i = 0 de 0 à a.T et i = j de a.T à T. Nous avons :
![]() (Eq.6)
(Eq.6)
condition de conduction permanente
Les interrupteurs unidirectionnels en courant imposent j ³ 0 donc J ³ 0; d'après l'expression de J, nous en déduisons une condition nécessaire de conduction permanente a > 1-E/U.
Cette condition n'est pas suffisante car on peut avoir une valeur moyenne positive avec un courant négatif sur un intervalle de la période. La condition nécessaire et suffisante est Jmin >0; d'après (Eq.3), nous en déduisons 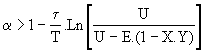 (Eq.7)
(Eq.7)
Si E et U sont constants avec E/U < 1, la condition nécessaire de conduction permanente ne peut être satisfaite lorsque a tend vers 0. Nous devons envisager le fonctionnement en conduction discontinue.
1.3 Étude en conduction discontinue
Ø De 0 à a.T, K conduit et le courant j augmente à partir de la valeur Jmin = 0.
L'équation j + t.dj/dt = E/R donne j = A.exp(-t/t) + E/R ;
le courant j est minimal en t =0; nous en déduisons Jmin = = 0 = A + E/R d'où j =E.[1-.exp(-t/t)] /R ; .
Le courant est maximal en a.T et vaut alors Jmax = E.(1-X)/R.
Ø De a.T à b.T , D conduit et impose v = U. Nous en déduisons comme en conduction permanente ![]() ; le courant s'annule en t = b.T soit en t' =(b-a).T; nous en déduisons :
; le courant s'annule en t = b.T soit en t' =(b-a).T; nous en déduisons : ![]() (Eq.8)
(Eq.8)
Ø De b.T à T, le courant j, ne pouvant être négatif, reste nul donc v = E.
La fig.3 donne l'allure des graphes : 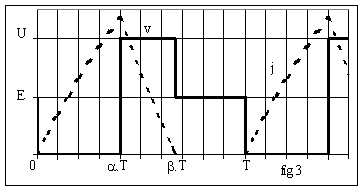
La valeur moyenne de v est V =(b-a).U+(1-b).E; celle du courant j est : ![]()
Nous calculons comme en conduction permanente la valeur moyenne du courant i:
![]() (Eq.9)
(Eq.9)
Comme lors de l'étude du hacheur série, nous constatons sur les graphes des figures 2 et 3 que le courant a une forme quasi linéaire. Lorsque la constante de temps t = L/R est grande devant la période T, nous pouvons confondre exp(-t/t) avec 1- t/ t.
2.1 Conduction permanente
De 0 à a.T, nous avons v = 0 = E -R.j-L.dj/dt. Si nous considérons que l'ondulation de j est faible devant la valeur moyenne J, nous pouvons confondre R.j(t) avec R.J; il vient alors : dj = (E-R.J).dt/L soit
j = (E-R).t/L+A. j(0) = Jmin = A et Jmax = j(a.T)= (E-R.J). a.T/L+A.
L'ondulation crête à crête est Dj = Jmax - Jmin = (E-R.J) a.T/L. La valeur moyenne de la tension v est
V = E-R.J=(1-a).U; nous en déduisons : Dj = a.(1-a).U/(L.f) (Eq.10); cette formule est semblable à celle du hacheur série; l'ondulation est maximale pour a = 0,5 et vaut U/4.L.f.
Le courant j étant de forme triangulaire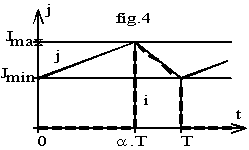
Nous avons J = (Jmax + Jmin) / 2 ; nous en déduisons : Jmax = J + Dj / 2 et Jmin = J - Dj / 2.
Le courant i a la forme d'un trapèze, nous en déduisons I = (Jmax + Jmin).(1-a)/ 2 = (1-a). J.
La puissance fournie par à la charge est P= (u.i)moy= U.I puisque u = Cste.
D'où P =(1-a). U.J = (1-a).[E-(1-a).U]/R. Pour E et R fixées, la puissance transférée à la charge est réglée par le rapport cyclique.
La condition de conduction permanent Jmin >0 soit J > Dj / 2. devient :
![]() (Eq.11); nous cherchons les racines du polynôme et nous savons que le polynôme est du signe du coefficient du terme de second degré, donc est positif) à l'extérieur des racines; nous en déduisons la valeur minimale de a permettant la conduction continue.
(Eq.11); nous cherchons les racines du polynôme et nous savons que le polynôme est du signe du coefficient du terme de second degré, donc est positif) à l'extérieur des racines; nous en déduisons la valeur minimale de a permettant la conduction continue.
2.2 Conduction discontinue
![]() ; en remplaçant exp(-t/t) par 1- t/ t, il vient j = E.t/R.t soit
; en remplaçant exp(-t/t) par 1- t/ t, il vient j = E.t/R.t soit
j = E.t /L; la valeur maximale du courant est j(a.T) = Jmax = a.E/L.f.
De a.T à b.T , ![]() ; soit en remplaçant exp(-t/t) par 1- t/ t :
; soit en remplaçant exp(-t/t) par 1- t/ t :![]() ; nous en déduisons la valeur de b en écrivant que j s'annule en t = b.T soit t' = (b-a).T :
; nous en déduisons la valeur de b en écrivant que j s'annule en t = b.T soit t' = (b-a).T : ![]() (Eq.12).
(Eq.12).
La fig.5 donne l'allure de j et i : 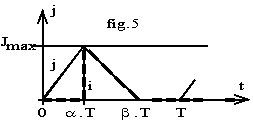
Nous avons en valeurs moyennes : V = (b-a).U+(1-b).E ; J = (E-V)/R ;
Compte tenu des formes triangulaires des courants j et i, nous en déduisons
J = b.Jmax / 2 et I = (b-a).Jmax / 2 = (b-a)J/b.
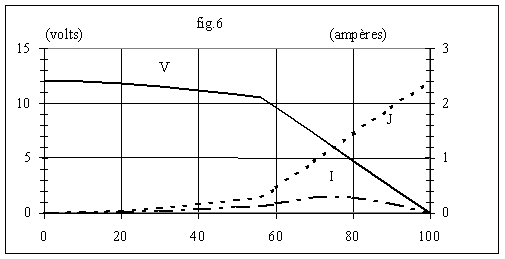
2.3 Exemple
On veut transférer de l'énergie d'une batterie de f.é.m E = 12 V à une autre batterie de f.é.m U= 24 V. On néglige la résistance des batteries. On donne de plus L = 1 mH ; R = 5 W.
La fréquence de découpage est f = 10 kHz .
Nous en déduisons t = L / R = 0,2 ms et T = 0,1 ms.
Sachant qu'en conduction continue, J = (E-V)/R et V = (1-a).U, la condition nécessaire de conduction permanente est J > 0 soit V < E donc 1-a< 0,5 ou a > 0,5.
Si a varie de 0 à 1, on doit envisager les deux régimes de fonctionnement.
calcul direct
On utilise les résultats du paragraphe 1.3. Calculons d'abord la valeur limite de a pour rester en conduction permanente.
Avec (Eq.7) nous calculons X.Y= exp(-T/t) = exp(-1/2)= 0,607 et a > 56,19 % pour rester en conduction permanente.
Pour a < 56,19 %, nous sommes en conduction discontinue; pour chaque valeur du rapport cyclique (Eq.8) donne b ; nous en déduisons V =(b-a).U+(1-b) ; J = (E-V)/R ; Dj = Jmax = E.(1-X)/R et I par (Eq.9).
Pour a > 56,19 %, nous sommes en conduction permanente, V=(1-a).U ; J = (E-V)/R ; Dj par (Eq.5) et I par (Eq.6).
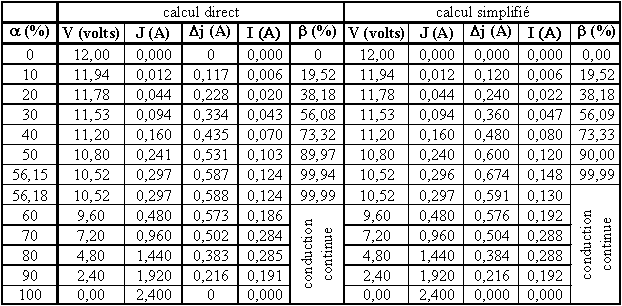
Le tableau ci-dessous donne les résultats.
calcul simplifié
Les racines de l'équation (Eq.11) sont -3,56 et 0,5616; la conduction est donc permanente pour
a > 56,16 %.
Pour a < 56,16 %, nous sommes en conduction discontinue; pour chaque valeur du rapport cyclique (Eq.12) donne b ; nous en déduisons V =(b-a).U+(1-b) ; J = (E-V)/R ; Dj = Jmax = = a.E/L.f. et I = (b-a)J/b.
Pour a > 56,16 %, nous sommes en conduction permanente, V=(1-a).U ; J = (E-V)/R ; Dj par (Eq.10) et
I =(1-a). J.
Le tableau ci-dessus donne les résultats.
La comparaison du calcul direct et du calcul simplifié montre une bonne concordance des résultats, bien que la constante de temps t soit seulement deux fois plus grande que la période.
L'écart sur les valeurs de J ne dépasse pas 4,5 % et celui sur les valeurs de Dj , 15 %
Lorsque la source est l'induit d'une machine à courant continu, nous pouvons négliger la résistance d'induit R et modéliser la source par un dipôle E - L. Les équations du hacheur ne permettent plus de calculer le courant moyen J; celui-ci est fixé par le couple de la machine.
Ø Conduction permanente : U, J, L, f et a étant fixés, nous pouvons calculer : V = E = (1-a).U ;
Dj = a.(1-a).U/(L.f) , Jmin = J- Dj /2 et Jmax = J+ Dj /2.
Nous devons vérifier que Jmin > 0 donc que J > Dj /2
Ø Conduction discontinue : V = E = (b-a).U+(1-b).E ; nous en déduisons b = a.U/(U-E).
Avec Jmax = a.E/L.f. = J /2.b, nous en déduisons : ![]() . U, J, L, f et a étant fixés, nous pouvons calculer E puis b .
. U, J, L, f et a étant fixés, nous pouvons calculer E puis b .
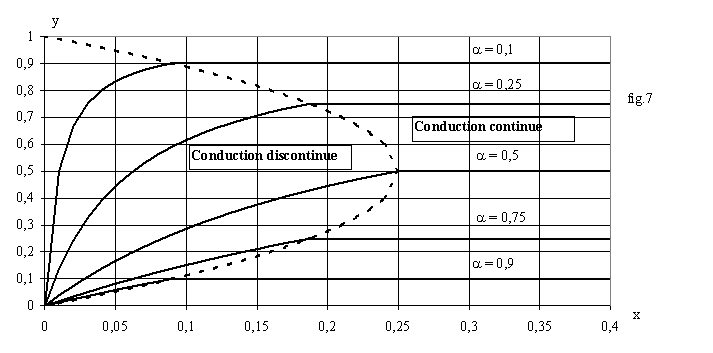
Comme pour le hacheur série, nous pouvons tracer les courbes de charge y(x) à a = Cste avec y = E/U et
x =2.L.f.J/U. Pour U, L et f donnés, y est proportionnel à E donc à la vitesse et x est proportionnel à J donc au moment du couple; ces courbes sont donc représentatives de la caractéristique mécanique de la machine continue.
En conduction permanente V = E = (1-a).U donc y = (1-a) = Cste.
En conduction interrompue ![]() donne y = x /(a²+x).
donne y = x /(a²+x).
La limite entre les deux régimes est obtenue pour J = Dj /2 soit J = a.(1-a).U/(2.L.f) ou encore x = a.(1-a).
Les courbes de charge sont tracées fig.7 :
Comme pour le hacheur série, nous constatons qu'en conduction permanente, il est possible de régler y donc la vitesse indépendamment de x donc du couple; en conduction discontinue, la vitesse varie avec le rapport cyclique mais aussi avec le couple.
Le plus souvent nous chercherons à rester en conduction permanente à tout régime; la valeur maximale de l'ondulation étant U/4.L.f, il suffit que le courant moyen reste toujours supérieur à U/8.L.f..
4.1 Principe
La source est modélisée par un dipôle E - r - L et la charge est une résistance fixe R.
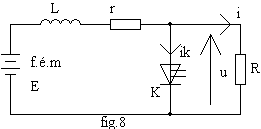
Lorsque K est passant, u = 0 donc i = 0; la diode D qui évitait la mise en court-circuit de la branche tension devient inutile. La structure est alors celle de la fig.8.
De 0 à a.T, K est fermé : le courant j tend vers la valeur E / r avec la constante de temps t = L / r.
De a.T à T, K est ouvert : le courant j tend vers la valeur E / R' , avec R' = r+R avec la constante de temps t'= L / R'.
Le courant j est donc toujours positif et nous sommes toujours en régime de conduction permanente.
4.2 Calcul direct
Ø De 0 à a.T, les équations du montage sont u = 0 ; i = 0 ; r.j+L.dj/dt = E.
Nous en déduisons j = E/r + A.exp(-t/t) .
Le courant étant minimal en t = 0, il vient ![]() .
.
A la fin de cette phase, le courant est maximal; en posant X = exp(-a.T/t) , nous obtenons :![]() (Eq.11).
(Eq.11).
Ø De a.T à T, les équations du montage sont u = R.i ; i = j ; (R+r).j+L.dj/dt = E. Nous en déduisons
j = E/R' + B.exp(-t'/t ') , en posant t’ = L/(R+r) et t' = t - a.T. Le courant dans L ne pouvant être discontinu, nous avons j (t'=0) = Jmax soit ![]() .
.
A la fin de cette phase, c'est à dire pour t = T donc t' = (1-a.)T, le courant en régime permanent périodique a repris sa valeur initiale j(0) = Jmin;
en posant Y' = exp[-(1-a).T/t '] , nous obtenons Jmin = Y'.Jmax + E.(1-Y')/R' (Eq.12).
Des équations (Eq.11) et (Eq.12), nous tirons les extremums du courant :
![]()
L'ondulation crête à crête est : ![]() .
.
Calculons les valeurs moyennes des courants :
![]()
Tous calculs faits, nous obtenons ![]() .
.
Pour un montage donné, I est fonction uniquement de a :
v pour a = 0, l'interrupteur K n'est jamais fermé donc en régime permanent, I = J = E/(R+r) ;
v pour a = 1, l'interrupteur K toujours fermé donc en régime permanent, I = 0 et J = E/r .
L'équation E = r.j+L.dj/dt+u donne en valeurs moyennes E = r.J+U = r.J+R.I; nous en déduisons
J = (E-R.I)/r .
Si nous avions directement branché le dipôle E-r-L sur une résistance variable Rh, nous aurions J = E/(r+Rh) Comme I varie avec a, J varie également avec a. Le hacheur parallèle chargé par R est équivalent à une résistance Rh variable de 0 à R lorsque a varie de 1 à 0.
4.3 Calcul simplifié
Les formules établies ci-dessus sont trop complexes pour donner des résultats facilement exploitables; nous allons simplifier le calcul en supposant que :
v la résistance r de la source est négligeable : nous prendrons donc r = 0 et R'=R
v la constante de temps t' = L/R' = L/R est très grande devant la période du hacheur T.
Avec ces hypothèses :
Ø de 0 à a.T : K conduit et u = 0 ; E = L.dj/dt d'où J = E.t/L+A; avec j(0) = Jmin, il vient j = Jmin + E.t/L.
A la fin de cette phase j(a.T) = Jmax = Jmin + E. a.T /L. Nous en déduisons l'ondulation crête à crête Dj = E. a.T /L = E. a /L.f.
Ø de a.T à T : K est ouvert et i = j ; E = R.j +L.dj/dt. Posons t' = t - a.T, le calcul est identique à celui fait directement; en faisant r = 0 dans l'expression obtenue du courant, nous obtenons : ![]() ; avec l'hypothèse t' << T, nous pouvons remplacer exp(-t'/t ') par 1-t'/ t ', il vient :
; avec l'hypothèse t' << T, nous pouvons remplacer exp(-t'/t ') par 1-t'/ t ', il vient : ![]() .
.
Écrivons que le courant est périodique en régime permanent : j(t=T) = j(t'=T-a.T) = j(t= 0). Nous en déduisons ![]() d'où
d'où
![]()
Les graphes de i et j sont semblables à ceux de la fig.4; nous en déduisons en valeurs moyennes :
![]()
E = U = R.I = R.J.(1-a) d'où J = E / [R.(1-a)]; si nous branchions directement une résistance variable Rh aux bornes de la source E-L, nous aurions J = E / Rh; nous en déduisons Rh = R.(1-a).
L'ensemble hacheur + résistance fixe R est donc équivalent à un rhéostat; la valeur de la résistance est réglée par le rapport cyclique a, sans déplacement d'un curseur d'où le nom de rhéostat statique donné à cette structure.
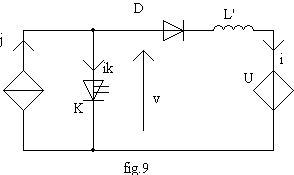
5.1 Charge E - R - L
Nous tenons compte de l'inductance parasité L' de la branche tension (fig.9) et nous modélisons la source par une branche idéale de courant continu J.
Nous étudions la conduction permanente.
Ø Fermeture de K
A t = 0-, K est ouvert et D conduit; nous supposons L' suffisamment faible pour que le régime permanent continu soit établi donc i = J et v = U.
A t = 0, nous commandons la fermeture de K
A t = 0+, i = J donc D conduit avec K qui impose le temps de montée du courant ik = J.t/ton.
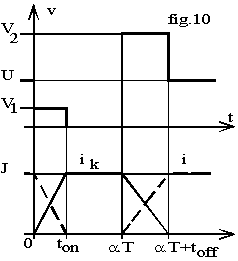
Pour t > 0, nous en déduisons i = J(1- t/ton) et v = U+L'.di/dt = U-L'.J/ ton = V1.
Deux cas peuvent alors se produire :
v V1 > 0, cas le plus fréquent représenté sur la fig.10, la fermeture de K se fait sous tension constante et la commutation est terminée en ton.
La commutation de K est d'autant plus dure, donc induit d'autant plus de pertes dans K, que V1 est proche de U.
v V1 < 0, dans ce cas, le mode de commutation dépend de la technologie de l'interrupteur K; si K ne peut conduire sous tension négative (cas du thyristor par exemple), le montage ne fonctionnera pas correctement.
Si l'interrupteur verrouille la tension à 0, nous aurons -L'.di/dt = U soit i = J-U.t/L' ; la commutation se termine pour i = 0 soit en t'on = L'.J/U et c'est l'inductance et la charge qui imposent la vitesse de croissance U/L' du courant ik. Ce fonctionnement risque d'être dangereux pour l'interrupteur K.
Nous devons donc nous assurer que V1 > 0.
Ø Ouverture de K
A t = a.T-, K est fermé et D est bloquée donc i = 0.
A t = a.T, on commande l'ouverture de K ; à t = a.T+, L' impose i = 0 donc ik = J.
Posons t' = t - a.T, pour t' > 0, K impose la décroissance du courant : ik = J(1-t'/toff); la continuité de J impose que D conduise : i = J-ik = J.t'/toff donc v = U+L'.di/dt = U+L'.J/toff = V2, valeur supérieure à U. L'interrupteur est donc soumis à une surtension au blocage.
L'inductance parasite :
v modifie la valeur moyenne de V; d'après la fig.10, on obtient
![]() au lieu de V=(1-a).U.
au lieu de V=(1-a).U.
v impose une surtension L'.J/toff à K lors de son ouverture
v crée des pertes de commutation dans K :
à la fermeture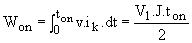 à l'ouverture
à l'ouverture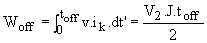
Faisons un exemple numérique : U = 150 V ; J = 20 A; L = 2 µH ; ton = 0,5 µs ; toff = 0,8 µs ; f = 10 kHz ;
a = 50 %. Nous en déduisons V1 = 70 V ; V2 = 200 V ; V = 75,5 V ; Won = 350 µJ ; Woff = 1 600 µJ.
La surtension est de 50 V à la fermeture soit 33 % de U; la valeur moyenne n'est quasi pas modifiée (75,5 V au lieu de 75 V); les pertes de commutation sont (Won + Woff).f = 19,5 W.
L'inductance parasite, comme pour le hacheur série, détériore le fonctionnement. Nous pouvons atténuer ces effets en plaçant une capacité C en parallèle sur la charge, au plus près du hacheur pour limiter l'effet des inductances de câblage. A l'ouverture, le condensateur assure la continuité de la tension v qui reste égale à U et permet l'extinction progressive du courant i; le choix du condensateur est identique à celui du hacheur série.
5.2 Rhéostat statique
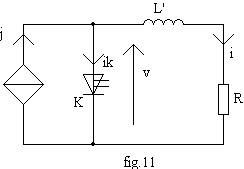
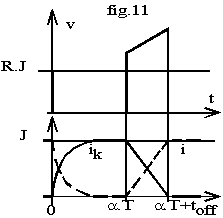
Dans ce cas, l'inductance parasite L' est due au câblage et à l'inductance propre de la résistance de charge R (fig.11).
Ø Fermeture de K
A t = 0-, K est ouvert; nous supposons L' suffisamment faible pour que le régime permanent continu soit établi donc i = J et v = R.J.
A t = 0, nous commandons la fermeture de K
A t = 0+, i = J; nous aurons deux cas suivant la rapidité de K:
v si K commute quasi instantanément, nous aurons v(0+)= 0 soit R.i.+L'.di/dt = ; en posant tp = L'/ R, il vient i = Aexp(-t/tp), soit avec la condition initiale :
i = J.exp(-t/tp) ; la charge impose donc la vitesse de croissance de ik = J.[1- exp(-t/tp)] égale au maximum à J/tp . Le temps de fermeture dure environ 5.tp jusqu'à annulation de i.
v si K impose une vitesse de croissance du courant ik inférieure à J/tp , ik = J.t/ton.
Pour t > 0, nous en déduisons i = J(1- t/ton) et v = R.i+L'.di/dt = R. J(1- t/ton)+L'. J.t/ton.
Dans ce cas, la fermeture de K se fait sous tension positive avec des pertes de commutation.
Ø Ouverture de K
A t = a.T-, K est fermé ; i = 0 et ik = J
A t = a.T, on commande l'ouverture de K ; à t = a.T+, L' impose i = 0 donc ik = J.
Posons t' = t - a.T, pour t' > 0, K impose la décroissance du courant : ik = J(1-t'/toff); i = J-ik = J.t'/toff donc v = R. J.t'/toff +L'. J./toff.
Durant l'ouverture, la tension v varie de L'. J./toff. à R.J+ L'. J./toff.
L'inductance L crée donc une surtension aux bornes de K et une commutation dure avec des pertes.
Faisons un exemple numérique :
R = 10 W ; J = 20 A; L = 2 µH ; ton = 0,5 µs ; toff = 0,8 µs ; f = 10 kHz ; a = 50 %.
A la fermeture tp = L'/ R = 0,2 µs et la vitesse de croissance de ik est J/tp =100 A / µs. En supposant que K puisse accepter cette vitesse, le temps de fermeture est de l'ordre de 1 µs.
A l'ouverture ik = 20.(1-1,25.106.t') et v = 250. 106.t' + 50 ; la tension varie de 50 à 250 V alors que R.J = 200 V; la surtension est de 50 V. Les pertes à l'ouverture sont :
![]() soit une puissance de 20 W.
soit une puissance de 20 W.
Nous ne pouvons dans ce cas, supprimer la surtension en plaçant un condensateur aux bornes de l'interrupteur car on modifierait la structure et on n'aurait plus un rhéostat statique. La surtension étant généralement de courte durée, nous pouvons protéger l'interrupteur par un dispositif écrêteur tel qu'une diode zéner ou une diode transil. La tension en régime continu aux bornes de K est R.Jmax; la tension d'écrêtage doit être supérieure à cette tension et inférieure à la tension maximale que peut bloquer K.
Reprenons l'étude du moteur de locomotive étudié au paragraphe 6 du chapitre 3.2.
6.1 Freinage rhéostatique
Nous faisons fonctionner la machine série en génératrice débitant sur un rhéostat statique et nous voulons exercer un couple de freinage T = 15 000 Nm pour une vitesse variant de 1 200 à 200 tr / min.
Le moment du couple électromagnétique est de la forme Tem = k.F(Is).I .
Pour passer de moteur en générateur sans inverser le sens de rotation, nous devons changer le signe du couple donc inverser un des courants Is et I. La seule solution est de croiser les connexions de l'induit ou celles de l'inducteur.
En utilisant des conventions générateur pour la machine, nous avons Tem = T - Tp; le moment du couple de pertes supposé constant étant Tp = 700 Nm, il vient
Tem = 14 300 Nm. La puissance électromagnétique de la machine est
Pem = E(Is).I = Tem.W = Tem.p.n/30 = 1497.n.
Si nous idéalisons le fonctionnement du hacheur, celui-ci est équivalent à une résistance variable
Rh = R.(1-a).
La résistance de la machine est R' = Ra+s.Rs/(s+Rs) = 25,5mW;
nous avons U = E(Is) - R'.I = Rh.I soit E(Is) =(Rh+R').I.
Pour la vitesse maximale, nous prenons a = 0 soit Rh = R. La puissance électromagnétique est
Pem = 1 796,4 kW = E(Is).I avec Is = 0,865.I. Pour calculer E et I, nous procédons par approximations successives; en nous donnant une valeur de Is, nous pouvons calculer I et lire sur la caractéristique à vide (Cf. Chapitre 3.2) la f.é.m Eo à la vitesse no = 800 tr/min. Nous en déduisons E = n.Eo/no et Pem. Nous essayons des valeurs jusqu'à obtenir la valeur voulue de la puissance électromagnétique. Par exemple pour
Is = 1000 A, I = 1 156 A et Eo = 1350 V, d'où E = 2 025 V et Pem = 2 341 kW; cette valeur étant trop forte, nous essayons une valeur plus faible de Is. Nous obtenons Is = 830 A ; I = 960 A et E = 1 875 V; nous en déduisons R = E/I - R' = 1,93 W.
Cette résistance doit dissiper R.I² = 1 777 kW.
A la vitesse minimale, pour le même couple, nous avons la même intensité I = 960 A.
Pem = 1497.n = 299,4 kW donc E = 312 V et Rh = E/I-R' = 0,3 W.
Nous en déduisons le rapport cyclique a = 84,5 %.
Le fonctionnement est donc possible mais la résistance R de 1,93 W dissipant 1 777 kW est difficile à réaliser.
Pour faciliter la réalisation de la résistance, nous devons diminuer sa valeur; pour garder la même puissance il faut augmenter l'intensité donc diminuer la f.é.m. Pour cela, on peut brancher la machine en excitation séparée. Si nous excitons la machine sous Is = 600 A = Cste, nous aurons Eo = 1 030 V et E = 1,29.n .A la vitesse maximale E = 1 548 V et I = Pem/E soit I = 1 160 A. La résistance de la machine est alors
R' = Ra= 19 mW; Nous en déduisons pour a = 0, la valeur de la résistance R = 1,32 W; nous gagnons 32 % sur la valeur de la résistance. A la vitesse minimale E = 258 V et I = 1 160 A soit Rh = 0,203 W et
a = 84,6 %.
6.2 Freinage en récupération
Nous pouvons, avec un hacheur élévateur, renvoyer l'énergie sur le réseau d'alimentation de tension
U = 1,5 kV.
Si nous utilisons la machine en excitation série, la source du hacheur est modélisée par la f.é.m E = n.Eo/no, l'inductance de filtrage L = 4,5 mH et la résistance R' = 25,5 mW.
Plaçons nous en conduction permanente, nous avons V = U(1-a) = E - R'.I; si nous négligeons la chute de tension R'.I, nous avons E = U(1-a) de valeur maximale 1 500 V.
A la vitesse maximale n = 1 200 tr/min, Eo = 1 000 V donc Is = 600 A et I = 694 A. La puissance électromagnétique maximale est donc Pem = E.I = 694 kW soit Tem = 5 523 Nm.
Nous ne pouvons donc obtenir le couple de freinage désiré à la valeur maximale.
Cherchons à partir de quelle vitesse nous pouvons atteindre le couple voulu.
Avec E =1 500 V, on se donne une vitesse n, on en déduit Eo donc Is sur la caractéristique à vide et
I = Is / 0,865. Nous en déduisons Pem et Tem que nous comparons à la valeur recherchée 14 300 Nm. Par exemple pour n = 1 000 tr / min, Eo = 1 200 V ; Is = 840 A , I = 971 A ,
Pem = 1456,5 kW et Tem = 13 910 Nm, valeur trop faible.
Par essais successifs, nous obtenons n = 960 tr / min et I = 960 A.
A la vitesse minimale, pour garder le même couple, nous gardons la même valeur de I donc de Is = 830 A et Eo = 1 250 V.
Nous en déduisons E = 312,5 V = 1500(1-a) soit a = 79,17 %.
Pour pouvoir obtenir le couple de freinage à la vitesse maximale, nous pouvons monter la machine en excitation séparée; pour pouvoir avoir une f.ém. E inférieure à 1 500 V à la vitesse n = 1 200 tr / min, il faut Eo < 1000 V soit Is < 600 A; si nous prenons Is = 500 A, nous avons Eo = 900 V soit E = 1 350 V, a = 10 % Pem = Tem.W = 1 797 kW donne I = 1 331 A.
En gardant I et Is constants, pour garder le même couple, à n = 200 tr / min , E = 225 V donc
a = 85 %. Nous pouvons donc répondre aux conditions exigées.