Électronique de puissance
xxxxxxModule 3 : xxxxxxx "Conversion DC - DC " |
Chapitre 3.2
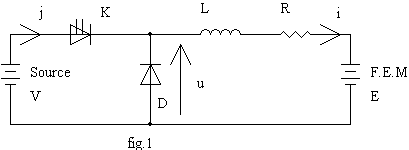
Hacheur série |
1 |
Peut-on utiliser la méthode simplifiée ? | La constante de la charge est t = L/R = 1 ms La période de découpage est T = 1 / f = 0,5 ms t = 2.T donc on ne peut pas utiliser la méthode simplifiée |
2 |
Calculer la valeur limite de a permettant la conduction permanente dans la charge | On doit avoir X.Y = exp(-a.T/t) . exp[-(1-a).T/t] = exp(-T/t) = 0,307 soit a > 30 % |
Le rapport cyclique est réglé à a = 80 % |
||
3 |
Calculer les valeurs moyennes de u, i | a > 30 % donc la conduction permanente est permanente U = a.V = 38,4 V La tension moyenne aux bornes de L étant nulle, I = (U - E) / R = 2,64 A |
4 |
Calculer les valeurs maximale et minimale de i | X = exp(-a.T/t) = 0,670 ; Y = exp[-(1-a).T/t] = 0,905 Imin = V.Y.(1-X)/R.(1-X.Y) - E / R = 2,44 A Imax = V.(1-X)/R.(1-X.Y) - E / R = 2,82 A |
Le rapport cyclique est réglé à a = 15 % |
||
5 |
Calculer la durée de conduction de la diode D |
X = 0,928 , Imax = 0,26 A , b = 54,2 % D conduit de a.T à b.T soit durant 196 µs |
6 |
Calculer les valeurs moyennes de u et i | U = a.V + (1-b).E = 12,7 V ; I = (U - E) /R = 70 mA |
1 |
Montrer que l'on peut utiliser la méthode simplifiée | La constante de la charge est t = L/R = 1 ms La période de découpage est T = 1 / f = 0,02 ms t >> T donc on peut utiliser la méthode simplifiée |
2 |
Déterminer la valeur minimale de a permettant la conduction continue | On doit avoir soit 480. a² + 47520.a - 12 000 = 0 Les racines de cette équation sont -9 925 % et 25,2 % Il faut donc a > 25,2 % |
3 |
Pour a = 80 % calculer les valeurs moyennes de u, i et j et l'ondulation crête à crête de i | On est en conduction permanente donc U = a.V = 38,4 V I = (U - E) / R = 2,64 A J = a.J = 2,11 A Di = a.(1-a).V / L.f = 15 mA |
4 |
Pour a = 15 % calculer les valeurs moyennes de u, i et j | On est en régime de conduction interrompue Imax = i(a.T) = (V-E). a.T / L = 10,8 mA b = a + (L.f . Imax )/( R.Imax+E) = 59,6 % I = b. Imax /2 = 3,2 mA ; U = E + R.I = 12,03 V
|
1 |
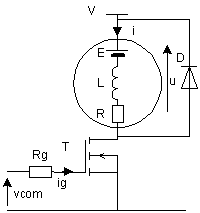
La machine fonctionne au point U = 240 V , I = 25 A et n = 1 500 tr/min. Calculer la constante K' et le moment du couple électromagnétique | E = U - R.I = 220 V ; K' = E / n = 0,147 Tem = K.I avec K = E / W = 30.K'/p = 1,4 V.s donc Tem = 35 Nm |
2 |
Le moment du couple de pertes, supposé constant est Tp = 4,5 A. Calculer l'intensité à vide Iv. |
Tem = K.Iv ; à vide Tu = 0 donc Tem = Tp Iv = Tp / K = 3,2 A
|
3 |
Déterminer la fréquence minimale de découpage pour que l'on fonctionne toujours en conduction permanente. |
Le courant moyen minimal est le courant à vide. L'ondulation crête à crête Di = a.(1 - a).V / L.f est maximale pour a = 50 % et vaut alors Dim = V/ 4.L.f La conduction est continue si Imin = I - Di /2 > 0 soit Di < 2.I On a donc V / 4.L.f < 2.Iv = 6,4 A soit f > V / 4.L.6,4 fmin = 11,7 kHz |
4 |
Dans toute la suite, le hacheur fonctionne à la fréquence f = 40 kHz. Pour le point de fonctionnement de la question 1, calculer le rapport cyclique et l'ondulation crête à crête du courant. |
U = a. V donc a = 80 % Di = a.(1 - a).V / L.f = 1,2 A |
5 |
Le rapport cyclique étant égal à 40 % et le courant moyen d'induit à 10 A, calculer la vitesse de la machine. | U = a. V = 120 V ; E = U - R.I = 112 V n = E / K' = 764 tr /min |
6 |
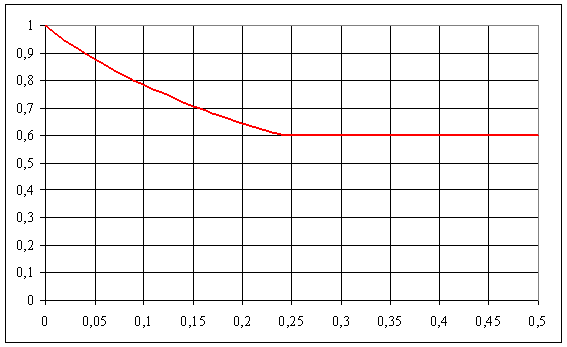
Tracer la courbe de charge du hacheur pour a = 60 % | On pose x = (2.L.f / V).I = 1,667.I et y = U / V = 0,0208.V Limite de conduction continue x = a(1-a = 0,24 soit I = 0,14 A Pour x < 0, 24 , soit y = (0,00994.x² - 0,0024.x +0,36) / ( 0,0994.x +0.36) Pour x > 0,24 , y = 0,6
|
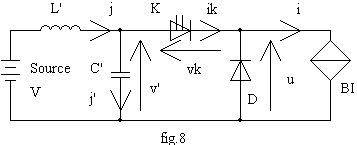
Calcul du filtre de ligne : on intercale entre la source et le hacheur un filtre de ligne L',C' suivant le schéma de principe ci-dessous :
on se fixe une ondulation de tension Dv' = 4 V et une ondulation de courant Dj = 0,2 A pour un courant dans la charge de 30 A |
||
7 |
Calculer la valeur de la capacité C' | Dv' = a.(1- a).I/C.f. Cette ondulation est maximale pour a = 0,5 et nous avons Dv' £ I / 4.C.f C = 46,9 µF soit C = 47 µF |
8 |
Calculer la valeur de l'inductance L' | Dj = a.(1-a) I /(8.f².L'.C'); la valeur de cette ondulation est maximale pour a = 0,5 soit Dj £ I / /(32.f².L'.C'). L = 62, 3 µH |
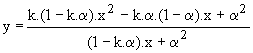 avec k = R/(2.L.f) = 0,01
avec k = R/(2.L.f) = 0,01