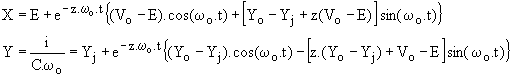Untitled Document

Principe

Lorsque nous étudions un circuit du second ordre, l'expression des solutions est complexe; en particulier il est difficile de trouver la valeur du temps qui correspond à une valeur donnée de la variable.

Dans de nombreuses applications, les circuits du second ordre étudiés sont des circuits R - L - C série de faible amortissement. Les variables d'état sont alors le courant i dans le circuit et la tension v aux bornes du condensateur, avec i = C dv/ dt.

Pour z << 1, le régime est de type oscillant amorti de pulsation propre w_o = 1/Ö (L.C)

La méthode du plan de phase consiste à utiliser les variables homogènes à des tensions : X = v et Y = C.w_o.i = i.Ö (L/C); le plan de phase est alors le plan rapporté à un système d'axes (X;Y) orthonormé. Il est alors possible de représenter simplement le graphe Y(X) du circuit et de le graduer en temps.

Circuit LC

Pour t = 0^-, K est ouvert et K' est en position 1; nous avons v(0^-)=vo et i(0^-)=I_o ; à t = 0, nous fermons K appliquant un échelon de tension continue E et, simultanément, nous basculons K en 2 , appliquant un échelon de courant continu J.

v et i sont les variables d'état du système donc v(0⁺) = vo et i(0⁺) =I_o

Pour t > 0, nous avons E = v + L di / dt , i_c = i - J = C dv / dt; d'où

v + L.C.v" = E.

La solution de l'équation est v = E + A.cos(w_ot)+B.sin(w_ot); nous en déduisons

i_c = C.dv/dt = C.w_o[B.cos(w_ot) -A.sin(w_ot)] et

i = i_c+J =J+ C.w_o[B.cos(w_ot) -A.sin(w_ot)].

Les conditions initiales donnent : vo =E + A et I_o = J + C.w_o.B .

Nous en déduisons :

v = E+(V_o-E).cos(w_ot)+[(I_o - J)/ C.w_o].sin(w_ot) et

i =J+(I_o-J).cos(w_ot)-[(V_o-E)/ C.w_o].sin(w_ot).

En utilisant les coordonnées du plan de phase et en posant

Y_o = I_o / C.w_o et Y_j = J / C.w_o , il vient :

X =E+(V_o-E).cos(w_ot)+(Y_o - Y_j).sin(w_ot) et

Y = Y_j +( Y_o - Y_j).cos(w_ot)-(V_o-E).sin(w_ot).

Nous avons : = r^².

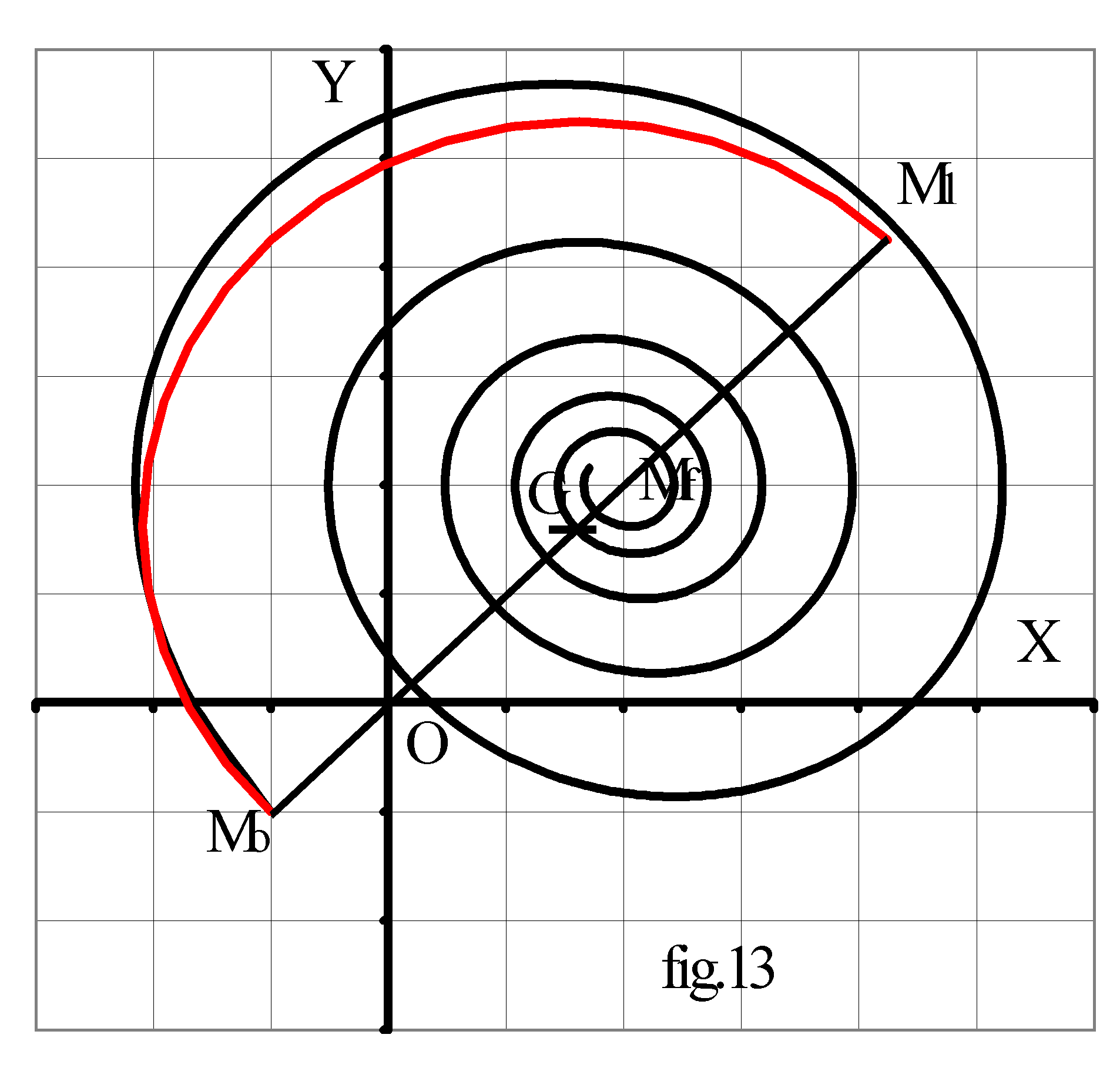
Cette équation est celle du cercle de centre G de coordonnées ( E ; Y_j ) et de rayon r . Ce cercle passe par le point initial M_o de coordonnées (vo ; Y_o). Lorsque le temps varie, le point M de coordonnées (X;Y) décrit le cercle dans le sens horaire à vitesse angulaire w_o :

Un circuit L-C soumis simultanément à des échelons de tension E et de courant J, a pour diagramme de phase Y(X) le cercle de centre G = (E ; J / C.w_o) passant par le point M_o = (Vo ; I_o / C.w_o). Ce cercle est décrit dans le sens horaire, à partir de M_o, à vitesse angulaire constante w_o

Circuit R-L-C de faible amortissement

Toute inductance réelle comporte une résistance de bobinage r. Prenons en compte cette résistance dans l'étude du circuit de la fig.11. Le facteur de qualité de la bobine est Q_o = L.w_o / r.

Pour t > 0, les équations du circuit sont E = v + L.i'+r.i ;

i_c= C.dv/dt = i -J.

Il vient donc : E = v +L.C.v"+r.C.v'+r.J soit

L.Cv" + r.C.v' + v = E - r.J. Nous avons donc w_o = 1 / Ö (L.C) et

z = r/2.L.w _o= 1 /(2.Q_o).

Si nous supposons l'amortissement faible soit z << 1 et Q_o >> 1, le régime transitoire est oscillant amorti :

v(t ) = avec w = w _o.Ö (1-z^²) et

Les conditions initiales donnent vo= E+A et

I_o = J+C.(w.B- z.A.w_o); nous en déduisons : A= V- E et

B = [I_o - J +C.z.w_o(vo E)]/ C.w.

Si nous supposons z << 1, nous pouvons confondre w et w_o.

Nous en déduisons : B = (I_o - J)/ C.w_o +z.(V_o- E) ,

C.(w.B- z.A.w_o) = I_o - J et

C.(w.A+z.w_o.B) = z.( (I_o - J)+C.w_o.(z^²+1)( vo- E) peu différent de

z.( (I_o - J)+C.w_o.( V_o- E).

Les solutions s'écrivent :

Dans le plan de phase, le graphe Y(X) est une spirale logarithmique (fig.13).

Graphe simplifié

Considérons la première pseudo-période de fonctionnement, soit

0 < t < p/w_o; l'amortissement étant faible, sur cet intervalle de temps, la spirale est peu différente du demi-cercle M_oM₁ ( trait rouge sur la fig.13). Déterminons les coordonnées de M₁:

X₁ = X(p/w_o) =

; Y₁ = Y(p/w_o) =

; en supposant p.z << 1, nous avons

; en posant

k = , nous obtenons X₁ =2.(1-k).E-(1-2.k).V_o et

Y₁ =2.(1-k).Y_j-(1-2.k).Y_o . M_oM₁ étant le diamètre du cercle, le centre G est au milieu du segment; ses coordonnées sont :

X_g = (X₁+X_o)/2 =(1-k).E+k.V_o et Y_g = (Y₁+Y_o)/2 =(1-k).Y_j+k.Y_o .

Comme dans l'étude à amortissement nul, le diagramme est parcouru dans le sens horaire à vitesse angulaire w_o :

Un circuit R - L - C de faible amortissement tel que p.z << 1, soumis simultanément à des échelons de tension E et de courant J, a pour diagramme de phase Y(X) approché sur l'intervalle de temps 0 < t < p/w_o le demi cercle de centre G = [(1-k).E+k.V_o ; (1-k).Y_j+k.Y_o)] passant par le point M_o = (vo ; I_o / C.w_o). Ce demi cercle est décrit dans le sens horaire, à partir de M_o, à vitesse angulaire constante w_o.