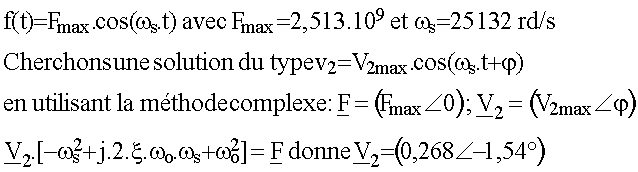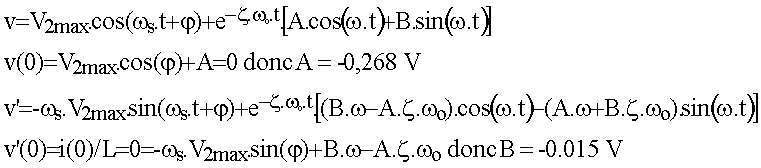|
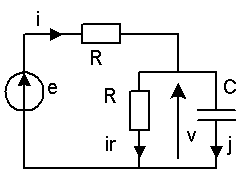
Quelles sont les variables d'état du système ? La seule variable d'état est la tension v
A t = 0, v = 2 V; déterminer les conditions initiales du réseau Calculons les grandeurs à t = 0+ :
v , variable d'état ne peut être discontinue : v(0+) = 2 V
ir(0+) = v/ R = 2 mA ; i = (e - v) /R ; e(0+) = 4 donc i(0+) = 2 mA
j = i - ir donc j(0+) = 0 ma
Pour t > 0, écrire les équations du réseau, en déduire l'équation différentielle donnant v(t) (1) e = R.i + v ; (2) i = j + ir ; (3) j = C.dv/dt ; (4) ir = v /R
on en déduit e = = R.(C.v' + v/R) + v
soit R.C.v' +2.v = e
Calculer la constante de temps du système La forme canonique de R.C.v' +2.v = e est :
v + (R.C/2).v' = e/2
La constante de temps est t = R.C/2 = 50 µs
Quelle est la solution générale de l'équation sans second membre Solution de l'équation sans second membre : v1 = A.exp(-t/t)
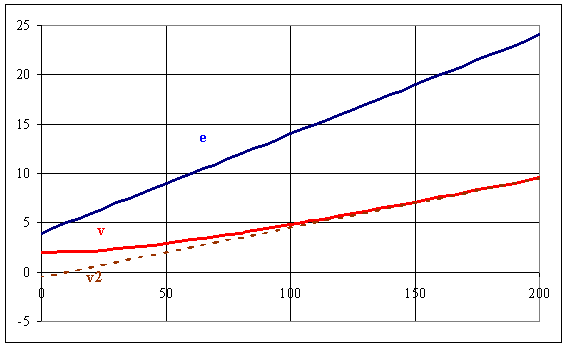
quelle est la solution particulière de l'équation complète f(t) = e/2 = 2 + 50 000. t, t étant en secondes
rechercher une solution du type v2 = a.t + b
si v2 = a.t + b ; dv2 /dt = a donc a.t + b +t.a = 2 + 50 000.t
par identification a = 50 000 et b = 2 - t.a = -0,5
v2 = 50 000.t(s) - 0,5 = 0,05.t(µs) - 0,5
En déduire v(t) v = v1 + v2 = A.exp(-t/t) + a.t + b
Avec t en µs : v = A.exp(-t/50) + 0,05.t - 0,5
v(0) = A -0,5 = 2 V donne A = 2,5 V
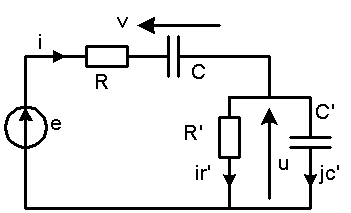
Tracer les graphes de ev(t) et v(t) Écrire les équations du réseau (1) i = ir' + jc' ; (2) e = R.i + v + u ; (3) i = C.dv/dt = C.v'
(4) jc' = C'.du/dt = C'.u' ; (5) u = R'.ir'
Montrer que u peut être calculée à partir d'une équation différentielle du second ordre (3), (4) et (5) donnent i = u/R' + C'.u'
Dérivons (2) : de/dt = e' = R.i' +v' + u'
i' = u'/R' + C'.u" et v' = i/C = u/R'.C + (C'/C).u'
e' = (R/R').u' + R.C'.u" + u/R'.C + (C'/C).u' + u'
R.C'.u" + (1+R/R'+C'/C).u' + u/R'.C = e'
calculer la pulsation propre et le coefficient d'amortissement Forme canonique : u" + 2.z.wo.u' +wo².u = f(t)
èfaire apparaître un coefficient 1 pour u"
u" + (1/R.C' + 1/R'.C' + 1/R.C).u' + u/(R.R'C.C') = e'/R.C'
èidentifier à la forme canonique :
wo = 1/Ö(R.R'C.C') = 550 rd/s
2.z.wo = (1/R.C' + 1/R'.C' + 1/R.C) soit z = 3,94
quelle est la forme de la solution générale u1(t) Le coefficient d'amortissement est supérieur à 1, la solution est de la forme A.exp(x1.t)+B.exp(x2.t)
x1 et x2 sont les racines de x²+ 2.z.wo.x +wo² = 0
soit x1 = -4262 et x2 = -71,1
quelle est la forme de la solution particulière u2 Le second membre est e' /R.C' = 0 ; la solution particulière est donc u2 = 0.
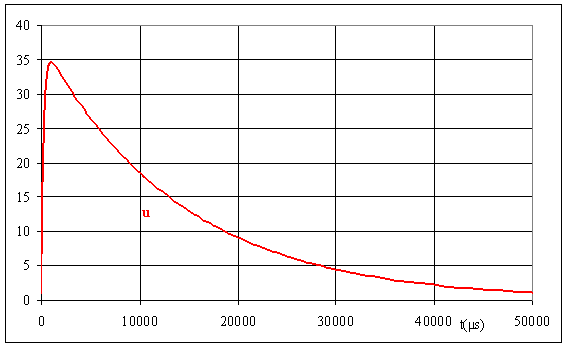
Donner les expressions de u(t) et v(t)
u = A.exp(x1.t)+B.exp(x2.t)
i = u/R' + C'.u' ; u' = A.x1.exp(x1.t)+B.x2.exp(x2.t)
i = A.(1/R'+C'.x1).exp(x1.t)+B.(1/R'+C'.x2).exp(x2.t)
v= e - R.i - u =
v = E - A.(R/R'+R.C'.x1-1).exp(x1.t)+B.(R/R'+R.C'.x2-1).exp(x2.t)
v = E - A'.exp(x1.t)- B'.exp(x2.t)
calculer les constantes A et B v(0) = 0 = E - A' - B' ; u(0) = 1 = A + B
A.(R/R'+R.C'.x1-1)+B.(R/R'+R.C'.x2-1) = 0
soit -2,31.A - 0,923.B = 0 et A + B = 1
B = -2,5.A ; A = -36,8 V et B = 37,8 V
Représenter u(t)
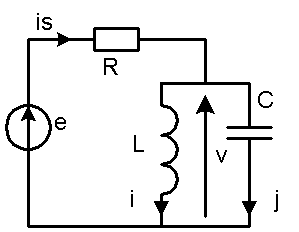
Écrire les équations du réseau (1) is = i + j ; (2) e = R.is + v ; (3) v = L.di/dt ; (4) j = C.dv/dt
En déduire l'équation différentielle donnant v(t) En dérivant (1) i's = i' + j ' = v/L + C.v"
En dérivant (2) : e' = R.i's + v' = R.v/L + R.C.v" + v'
soit R.C.v" + v' + (R/L).v = e'
calculer la pulsation propre et le coefficient d'amortissement Divisons l'équation par R.C pour obtenir la forme canonique :
v" + (1/R.C).v' + (1/LC).v = e' /(R.C)
wo = 1/Ö(L.C) =100 000rd/s
2.z.wo = 1/R.C soit z = 0,05
quelle est la forme de la solution générale u1(t) Le coefficient d'amortissement étant z < 1 , la solution est :
v2 = exp(-z.wo.t). [A.coswt+B.sinwt] avec
w = wo.Ö(1-z²) = 99 875 rd/s
quelle est la forme de la solution particulière u2 Le second membre est f(t) = e'/(R.C) = [10.2.p.fs/(R.C)].cos (2.p.fs.t)
soit f(t) = Fmax.cos(ws.t)
Donner l'expression de v(t)
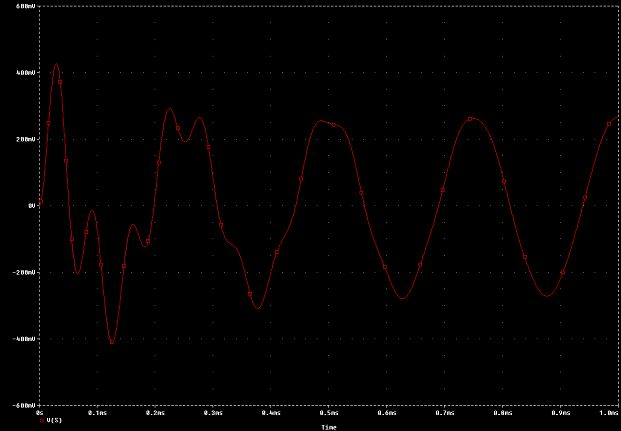
Graphe de v(t)
A t = 0, Tp conduit seul; tous les courants sont nuls sauf ip = I = Cste; v = -E. On amorce alors le thyristor Te. Montrer que, durant une première phase, Tp et Te conduisent seuls. ip est une variable d'état (courant dans L) donc ip(0+) = I donc Tp conduit
v est une variable d'état et ve = 0 donc u = E - v = 2.E donc D est bloquée
Ti n'a pas été amorcé et de plus il est polarisé négativement donc ne peut conduire
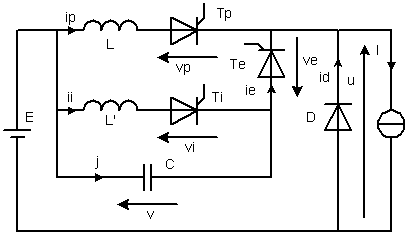
Utiliser la méthode du plan de phase appliqué au circuit L - C pour étudier les variations de v et j ip + ie = ip + j = I = Cste donc j(0) = 0
Le circuit L -C dans l'état initial v = -E et j = 0 est mis en court-circuit par Tp et Te donc soumis à un échelon de tension nul et à aucun échelon de courant
Posons X = v et Y = j.Ö(L/C)= 0,316.j, wo = 1/Ö (L.C) = 15 811 rd/s
Le diagramme de phase Y(X) est un cercle de centre (0;0), passant par le point initial Mo = ( -E ; 0)
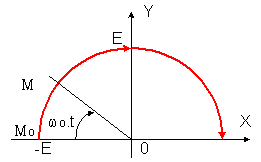
Montrer que Tp se bloque en t = t1. Y va évoluer de 0 à 1 500 V puis revenir à 0
j= Y/0,316 augmente donc de 0 à 4 743 A et ip = I- j évolue de
2 000 à -2 473 A. Or Tp se bloque lorsque ip = 0 soit j = j1 = I et Y = Y1 = 632 V
Tp se bloque donc en t1 : X² + Y² = E² donc X1 = -1 360 V et
tg(wo.t1) = |Y1 /X1| = 0,464 et t1 = 27,5 µs
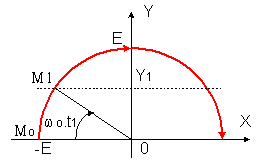
montrer que te conduit seul pour t > t1. En déduire l'évolution de v et l'instant t2 de blocage de Te A t = t1, v = -1 360 V donc u = E - v = 2 860 V et u > 0 interdit la conduction de D; Ti ne peut être amorcé tant que v < 0
donc te conduit seul pour assurer la continuité de I
j = ie = I = C.dv.dt donc v = I.t/C + A
v(t1) = - 1360 V donc v = I.(t-t1)/C - 1360 V
u = E - v = 2860 - I.(t-t1)/C s'annule en t2 tel que
t2-t1 = 2 860.C/I = 572 µs soit t2 = 600 µs
D se met alors à conduire v(t2) = E ; Te est polarisé légèrement négativement par D donc se bloque.
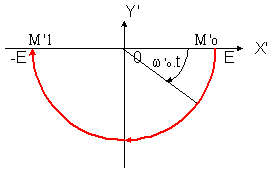
A t = T = 1 500 µs , on amorce Ti, Tp et te sont bloqués. On pose t' = t - T. Quel est le diagramme de phase Y'(X') du réseau L'.C ? ii + j = 0
Le circuit L' -C dans l'état initial v = E et j = 0 est mis en court-circuit par Ti
donc soumis à un échelon de tension nul et à aucun échelon de courant
posons X' = v et Y' = j.Ö(L'/C)= j, w'o = 1/Ö (L'.C) = 5 000 rd/s
Le diagramme de phase Y'(X') est un cercle de centre (0;0), passant par le point initial M'o = ( E ; 0)
montrer que Ti se bloque en t' = t'3. Ti ne peut conduire que si j donc Y' sont négatifs; il se bloque donc en M'1 soit en w'o.t'3 = p soit t'3 = 628 µs