|
1 Conditions initiales d'un réseau
1.1 Principe et technologie
Dans la réalité, un réseau n'est jamais alimenté en permanence ou sa structure se modifie par la manœuvre d'interrupteurs. Si à un instant t = to on modifie l'état d'un interrupteur, l'état électrique du réseau va changer : pour t< t0 , on a un régime de fonctionnement et pour t > to un autre régime défini par de nouvelles équations.Parmi les grandeurs ou variables du réseau, on distingue :
Ø les variables d'état qui ne peuvent être discontinues : tension aux bornes d'un condensateur, courant dans une inductance, f.é.m d'une batterie …
Ø les autres variables qui peuvent être continues ou discontinues : courant dans un condensateur, tension aux bornes d'une inductance …
On connaît généralement l'état du réseau "juste avant" l'instant t0 où on modifie le régime; déterminer les conditions initiales du régime après modification c'est déterminer la valeur de toutes ses variables "juste après" to . En pratique, on distinguera
; on considérera que toute variable d'état y(t) ne peut varier entre ces deux instants :
1.2 Méthode de calcul
Connaissant toutes les variables à
, on connaît toutes les variables d'état à
puisqu'elles n'ont pas varié; on écrit alors les équations du réseau dans le nouveau régime et on en déduit la valeurs des variables à
.
.
ExempleÉtudions le circuit de la figure ci-dessous :
Pour t < 0, l'interrupteur K est ouvert et le circuit est au repos : toutes les grandeurs sont nulles sauf E.
A t = 0, on ferme K.
Les variables d'état sont E, v' et i. Nous en déduisons :

Pour K fermé, les équations du réseau sont :
(1) i = i' + i" ; (2) E = R.i + v + v' ; (3) v' = R'.i"
De (3), nous déduisons
; en portant cette valeur dans (1), il vient
;
l'équation (2) donne

Nous constatons que seule la variable v est discontinue; i' est continue bien que ce ne soit pas une variable d'état.
2 Méthodes de résolution des équations différentielles
Les réseaux linéaires sont décrits par des équations linéaires à coefficients constants de la formeou an, …ao sont des constantes et n l'ordre de l'équation.
Pour résoudre ce type d'équation décrivant un régime à partir de l'instant to, nous devons :
Ø étape 1 : mettre l'équation sous forme canonique, c'est à dire sous une forme qui ne dépend plus que de l'ordre de l'équation sans faire intervenir les expressions des coefficients, le type de variable, la forme de g(t) …
Ø étape 2 : résoudre l'équation sans second membre, c'est à dire l'équation obtenue en annulant g(t). La forme générale de cette solution est fonction du degré de l'équation. Nous obtenons alors une fonction y1(t) qui contient n constantes arbitraires dites constantes d'intégration.
Par exemple si nous avons d²y / dt² = 3 , l'intégration de la constante donne : dy / dt = 3.t + A, A étant une constante arbitraire, ce qui veut dire que 3.t+ 10 est solution de même que 3.t - 5.p par exemple. Une nouvelle intégration donne y(t) = 1,5.t² + A.t + B. On introduit donc une deuxième constante arbitraire B.
La fonction y1(t) est appelée solution générale de l'équation sans second membre (S.G.E.S.S.M. en abrégé) en raison de la présence des constantes.
Ø étape 3 : chercher une solution de l'équation avec second membre, c'est à dire trouver une fonction y2(t), entièrement définie sans constante arbitraire, satisfaisant à l'équation à résoudre. Cette recherche se fait généralement par identification; on se donne une fonction ayant la "même forme mathématique" que le second membre g(t), c'est à dire si g = Cste , on prend y2(t) = Cste, si g est un polynôme de degré n, y2(t) est un autre polynôme de même degré, si g est une fonction sinusoïdale, y2(t) est une fonction sinusoïdale de même fréquence…
La fonction y2(t) contient des valeurs arbitraires ; on calcule les dérivées successives de y2(t) et on identifie les deux membres de l'équation; identifier veut dire que l'égalité est vraie pour toute valeur de la variable temps; cette identification permet de calculer les valeurs arbitraires introduites dans y2(t).
Prenons par exemple : 3. y' + 2.y = 5.t² + 1 , y' représentant la dérivée première dy/dt. Le second membre étant un polynôme de degré 2, nous cherchons y2(t) de la forme a.t²+b.t + g. Nous en déduisons y'2(t)= 2.a.t+b ; l'équation différentielle donne :
3.(2.a.t+b)+2.(a.t2+b.t + g) = 5.t² + 1 soit 2.a.t² +(6.a+2.b)t +3.b + 2.g = 5t² + 1. Deux polynômes sont identiques si les coefficients des termes de même degré sont égaux; nous en déduisons 2.a = 5 soit a.=2,5 ; 6.a+2.b = 0 soit b = -3.a = -7,5 ; 3.b + 2.g = 1 soit g = 11,25.
Nous en déduisons y2(t) = 2,5.t² - 7,5.t + 11,25.
Ø étape 4 : la solution générale de l'équation différentielle (en abrégé S.G.E.A.S.M) est la somme des fonctions obtenues aux étapes 2 et 3 : y(t) = y1(t) + y2(t).
Ø étape 5 : la solution y(t) contient n variables arbitraires; il y a donc une infinité de solutions; ceci est satisfaisant mathématiquement mais pas physiquement; en partant d'un état initial donné, un réseau électrique ne peut évoluer d'une infinité de façons; à chaque instant la solution doit être unique, ce qui veut dire qu'il y a un seul ensemble de constantes d'intégration tel que les variables du réseau aient leurs valeurs initiales à l'instant initial où les équations s'appliquent. Nous utiliserons les valeurs initiales de la fonction y(t) et de ses dérivées successives pour calculer les constantes arbitraires.
Nous allons préciser tout ceci sur des exemples.
3 équation différentielle du premier ordre
3.1 Forme canonique
Cette équation se présente sous la forme a.y' + b.y = g(t) avec y' = dy/dt.
Si le coefficient a est nul, l'équation donne y = g(t)/b ; si b est nul, y' = g(t)/a, se résout par la recherche de la primitive de g(t). Nous supposons donc que a et b sont différents de 0.
La forme canonique de l'équation du premier ordre est : y + t. y' = f(t) caractérisée par un coefficient 1 pour la fonction y(t). Pour l'obtenir, il suffit donc de diviser les deux membres de l'équations par b : (a/b) y' + y = g(t) / b donc t = a / b et f(t) = g(t) / b.
La constante t est appelée constante de temps du système en raison de l'unité dans laquelle elle s'exprime qui est l'unité de temps soit la seconde.
3.2 Equation sans second membre
Nous avons y + t. dy/dt = 0 soit dy / y = - dt / t ; la primitive de dy / y est Ln(y) et celle de dt est t; il vient donc Ln(y) = - t / t + A', A' étant la constante d'intégration. La fonction inverse du logarithme népérien étant la fonction exponentielle, il vient
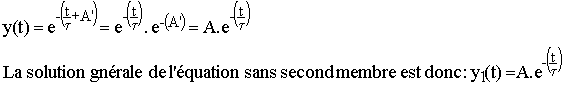
3.3 Solution particulière
Envisageons la solution particulière y2 de y + t. y' = f(t) pour diverses formes de f(t) :
v f(t) = Cste = F ; y2(t) = K = Cste donc y' = 0; en reportant dans l'équation nous avons K = F.v f(t) = a'.t + b' ; y2(t) = a.t+b donc y'2(t) = a ; en reportant dans l'équation, il vient :a.t+b + t. a = a'.t + b' soit a = a' et b + t. a = b' soit +b = b' - t. av; nous cherchons une fonction sinusoïdale de même pulsation donc de forme générale
; nous savons que pour les circuits linéaires, la méthode complexe permet de remplacer les équations différentielles par des équations linéaires; appliquons cette méthode; à f(t) on associe
, à y2(t) on associe
et à dy2 / dt on associe j.w.Y2. D'où :
3.4 Solution générale
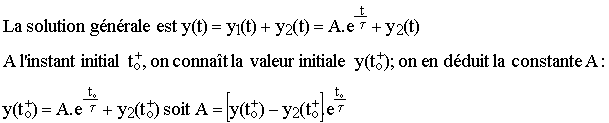
3.5 Exemples
Circuit RC
Étudions le réseau ci-contre : 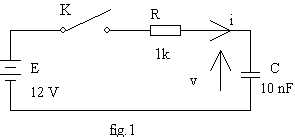
Pour t < 0 , K est ouvert et C est chargé sous v = Vo = -10 V.
Pour K fermé, on a E = R.i + v avec i = C.dv /dt soit
R.C.dv/dt + v = E; l'équation est directement obtenue sous forme canonique avec t =R.C= 10µs.

La fig.3 représente les graphes de v et de i.
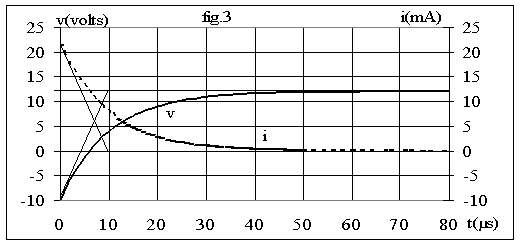
Remarques
on peut rapidement tracer une fonction exponentielle à l'aide de deux propriétés; soit la fonction y(t) = A.exp(-t/t) + B ; pour t ® ¥ ,
y(t)® B = y(¥); pour t = 0, y(0)=A+B; on peut donc écrire y(t) = [y(0)-y(¥)]exp(-t/ t) + y(¥);
v pour t = 5. t, exp(-t/ t) = 0,7 % donc y(t) est peu différent de y(¥);
v cherchons la tangente à l'origine, droite de la forme z = a.t + b; a = dy(0) / dt
En traçant la tangente à l'origine et en sachant que le graphe passe par le point [t=5.t ; y= y(¥)] on obtient un tracé rapide et assez précis du graphe
Circuit RL
Étudions l'établissement d'un régime sinusoïdal dans un circuit R-L : alimentons en série une résistance R = 50 W et une inductance L = 1 H par un générateur e tel que pour t < 0 e = 0 et pour t > 0 e = ![]() avec E = 10 V , f = w /2.p = 50 Hz et y = 60°.
avec E = 10 V , f = w /2.p = 50 Hz et y = 60°.
Nous supposons le circuit au repos pour t < 0, c'est à dire que le courant i dans le circuit et la tension v aux bornes de L sont nuls.
i(t) étant variable d'état, i(0+) = 0. Pour t > 0 nous avons e = R.i + v = R.i + Ldi/ dt; l'équation sous forme canonique est donc i + t. di / dt = e(t) / R avec t = L / R = 20 ms.
La solution générale de l'équation sans second membre est i1(t) = A.exp(-t/t).
Cherchons une solution particulière de l'équation sans second membre sous la forme
i2(t) = ![]() en utilisant la méthode complexe; nous obtenons R.I2 +jLw. I2=E;
en utilisant la méthode complexe; nous obtenons R.I2 +jLw. I2=E;
Z = R + jLw = (318 W ; 81°); il vient donc I2 = E / ||Z|| =31,4 mA et arg I2 = j = -21° soit j = -0,366 rd ; nous en déduisons i2 = 44,5 cos(w.t - 0,366).
La solution générale de l'équation est i = A.exp(-t/t) + 44,5 cos(w.t - 0,366).
La condition initiale i(0) = 0 donne A = -44,5 cos(-0,366) = -41.5 mA. La fig.4 donne l'allure du graphe
.

Remarque
dès que t > 5.t, le terme exponentiel est négligeable et on obtient un régime permanent sinusoïdal; la déformation du courant par rapport au régime sinusoïdal durant la phase transitoire dépend de la valeur de A = I2.Ö2.cos( y -jz ), jz étant l'argument de Z.
Le régime transitoire n'existe plus si A = 0 soit y - jz = p / 2.
Si le circuit est très inductif, c'est à dire si L.w >> R, jz est peu différent de p / 2 et le régime sinusoïdal s'établit instantanément si y = 0; on a alors e(0) = E.Ö2= Emax c'est à dire qu'on applique la tension e(t) lorsque celle-ci est maximale.
4 equation différentielle du second ordre
4.1 Forme canonique
L'équation se présente sous la forme a.y" + b.y' + c.y = g(t) avec y" = d²y/dt² et y' = dy/dt ; nous supposons que a est différent de 0 (si a = 0, l'équation est d'ordre 1).
La forme canonique de l'équation du deuxième ordre est caractérisé par un coefficient 1 pour la dérivée seconde; en divisant par a, il vient y" + (b/a).y'+ (c/a).y = g(t)/a ; posons ![]() ; f(t) = g(t)/a nous obtenons la forme canonique :
; f(t) = g(t)/a nous obtenons la forme canonique : ![]() wo est la pulsation propre du système et z le coefficient d'amortissement.
wo est la pulsation propre du système et z le coefficient d'amortissement.
4.2 Équation sans second membre
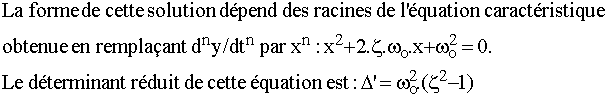
Nous avons trois cas suivant le signe du déterminant :
Ø régime apériodique : si le déterminant est positif soit si z > 1, l'équation caractéristique a deux racines réelles négatives :
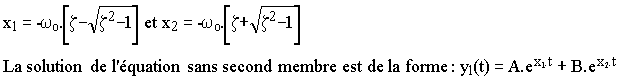
Ø régime apériodique critique : si le déterminant est nul, soit si z = 1, l'équation caractéristique a une racine double - z . wo = - wo.
![]()
Ø régime oscillant amorti : si le déterminant est négatif, soit si z < 1, l'équation caractéristique a deux racines complexes conjuguées x = -z.wo ±j.w avec w = wo.Ö(1-z²);![]()
4.3 Solution particulière
La méthode de recherche est la méthode générale :
v si f(t) = F = Cste on cherche y2 = K = Cste; on a alors y'2 = y"2 = 0 soit K = F / wo².
v si f(t) = a'.t + b' ; y2(t) = a.t+b donc y'2(t) = a ; y"2(t) = 0; en reportant dans l'équation, il vient : ![]() ; en égalant les coefficients des termes de même degré, on obtient :
; en égalant les coefficients des termes de même degré, on obtient : ![]()
v ![]() ; nous cherchons une fonction sinusoïdale de même pulsation donc de forme générale
; nous cherchons une fonction sinusoïdale de même pulsation donc de forme générale ![]() ; nous savons que pour les circuits linéaires, la méthode complexe permet de remplacer les équations différentielles par des équations linéaires; appliquons cette méthode; à f(t) on associe
; nous savons que pour les circuits linéaires, la méthode complexe permet de remplacer les équations différentielles par des équations linéaires; appliquons cette méthode; à f(t) on associe![]() , à y2(t) on associe
, à y2(t) on associe ![]() , à dy2/ dt on associe j.W. Y2 et à d²y2 / dt² on associe -W². Y2.
, à dy2/ dt on associe j.W. Y2 et à d²y2 / dt² on associe -W². Y2.
Il vient donc :  ; nous pouvons en déduire module et argument de Y2 .
; nous pouvons en déduire module et argument de Y2 .
4.4 Solution générale
La solution générale y(t) = y1(t)+y2(t) contient deux constantes arbitraires; ces constantes sont calculées à partir des valeurs initiales y(0+) et y'(0+).
4.5 Exemple
Étudions le circuit de la fig.5 :
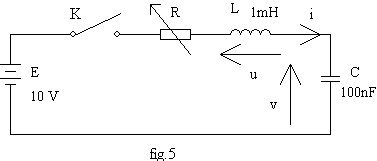
.
Pour t < 0, K est ouvert donc i = 0 et le condensateur est chargé sous la tension vo = - 5 V.
A t = 0, on ferme K.
Cherchons les conditions initiales:
v et i sont variables d'état donc v(0+)=vo et i(0+)=0. Les équations du réseau sont E = R.i + u + v ;
i = C.dv/dt et u = L.di/dt.
Nous en déduisons u(0+)= E-Vo = 15 V.pour t > 0, il vient E = R.C.v' + L.C.v" + v ; on obtient la forme canonique en divisant par L.C soit en posant
wo = 1 / Ö(L.C) et z=R/2.L.wo=R.Ö(C/L) / 2 : v" +2.z .wo.v' + wo² .v = wo² .E
Numériquement wo = 105 rd/s et z = R / 200 .
Cherchons la solution générale de l'équation
Ø Premier cas : R = 1 kW ; z = 5 > 1, nous sommes donc en régime apériodique; les solutions de l'équation caractéristique sont x1 = -10 102 s-1 et x2 = -989 898 s-1 . La solution générale de l'équation sans second membre est ![]() .
.
Le second membre étant constant, nous avons v2(t) = E.
La solution générale est v(t) = E + ![]() .
.
Nous en déduisons i(t) = C.dv / dt = ![]() ;
;
u = L.di/dt = ![]() .
.
Les conditions initiales v(0+) = -5 V = E + A + B et i(0+) = 0 = C.x1.A+C.x2.B donnent A = -15,15 V et B = 0,15 V;
il vient : v = 10 ![]() volts, i =
volts, i = ![]() ; u =
; u = ![]() .
.
La fig.6 donne l'allure des graphes :
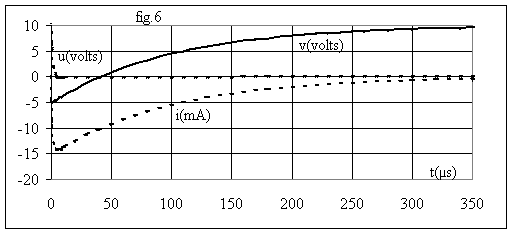
On constate que pour la tension v, la valeur de régime permanent v = E = 10 V est atteinte à 5% près pour tf = 338 µs.
Si nous considérons les constantes de temps t1 = -1 / x1 = 99 µs et t2 = -1 / x2 = 1 µs, on constate que tf est de l'ordre de trois fois la plus grande des deux constantes de temps.
Ø Deuxième cas : R = 200 W ; z = 1, nous sommes donc en régime apériodique critique ; la solution est v(t) = ![]() ; nous en déduisons
; nous en déduisons
i = C.dv/dt= ![]() ; u = L.di/dt =
; u = L.di/dt = ![]()
Les conditions initiales donnent v(0+) = -5 V = E + B et i(0+) = 0 = C(A-B.wo) ; nous en déduisons B = -15 V et A = -15.105 V.s-1. Les solutions sont finalement :
v = ![]() volts ; i =
volts ; i = ![]() ampères ; u =
ampères ; u = ![]()
La fig.7 donne l'allure des graphes :
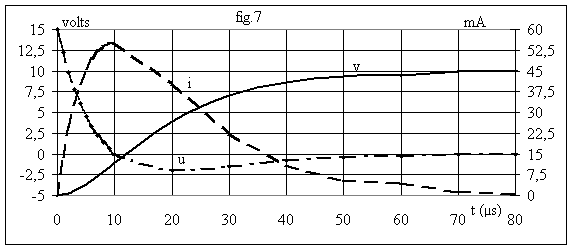
On constate que le régime permanent est atteint à 5 % près pour t = 52,3 µs.
.
Ø Troisième cas : R = 100 W ; z = 0,5; nous sommes donc en régime oscillant amorti ; la solution est v(t ) = ![]() avec w = wo.Ö(1-z²) = 86 600 rd/s.
avec w = wo.Ö(1-z²) = 86 600 rd/s.
Nous en déduisons :
![]()
![]()
Les conditions initiales v(0+) = -5 V = E + A et i(0+) = 0 = C(w.B- z.A.wo) donnent A = -15 V et
B = -8,66 V.
Nous en déduisons : v(t) = ![]() volts;
volts;
i(t) = ![]() mA ; u(t) =
mA ; u(t) = ![]() volts.
volts.
La fig.8 donne l'allure des caractéristiques :
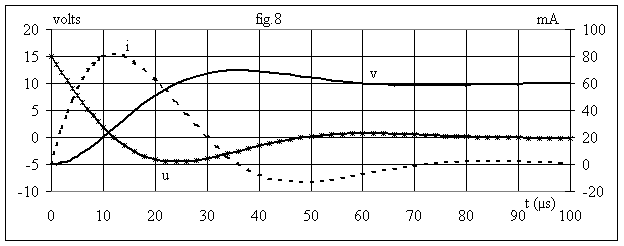
On constate que le régime permanent est atteint à 5 % près ( v reste compris entre 9.5 et 10,5 volts) pour t = 55 µs.
Le temps d'établissement du régime permanent dans un réseau du second ordre est minimal pour le régime apériodique critique, c'est à dire lorsque le coefficient d'amortissement est égal à 1.
5.1 Principe
Lorsque nous étudions un circuit du second ordre, l'expression des solutions est complexe; en particulier il est difficile de trouver la valeur du temps qui correspond à une valeur donnée de la variable; la résolution de l'équation y(t) = Y1 ne peut se faire directement, il faut procéder soit graphiquement, soit numériquement par essais successifs de valeurs du temps.
Dans de nombreuses applications, les circuits du second ordre étudiés sont des circuits R - L - C série de faible amortissement. Les variables d'état sont alors le courant i dans le circuit et la tension v aux bornes du condensateur, avec i = C dv/ dt.
Pour z << 1, le régime est de type oscillant amorti de pulsation propre wo = 1/Ö (L.C)
La méthode du plan de phase consiste à utiliser les variables homogènes à des tensions : X = v et
Y = C.wo.i = i.Ö (L/C); le plan de phase est alors le plan rapporté à un système d'axes (X;Y) orthonormé. Il est alors possible de représenter simplement le graphe Y(X) du circuit et de le graduer en temps.
5.2 Réponse d'un circuit LC à des échelons simultanés de tension et de courant
Étudions le circuit L-C de résistance nulle représenté sur la fig.11.

Pour t = 0-, K est ouvert et K' est en position 1; nous avons v(0-)=vo et i(0-)=Io ; à t = 0, nous fermons K appliquant un échelon de tension continue E et, simultanément, nous basculons K en 2 , appliquant un échelon de courant continu J.
v et i sont les variables d'état du système donc v(0+) = vo et i(0+) =Io
Pour t > 0, nous avons E = v + L di / dt , ic = i - J = C dv / dt; J étant constant, dic/dt = di/dt d'où
v + L.C.v" = E. Le coefficient d'amortissement étant nul, la solution de l'équation est
v = E + A.cos(wot)+B.sin(wot); nous en déduisons ic = C.dv/dt = C.wo[B.cos(wot) -A.sin(wot)] et
i = ic+J =J+ C.wo[B.cos(wot) -A.sin(wot)].
Les conditions initiales donnent : vo =E + A et Io = J + C.wo.B . Nous en déduisons :
v = E+(Vo-E).cos(wot)+[(Io - J)/ C.wo].sin(wot) et i =J+(Io-J).cos(wot)-[(Vo-E)/ C.wo].sin(wot).
En utilisant les coordonnées du plan de phase et en posant Yo = Io / C.wo et Yj = J / C.wo , il vient :
X =E+(Vo-E).cos(wot)+(Yo - Yj).sin(wot) et Y = Yj +( Yo - Yj).cos(wot)-(Vo-E).sin(wot).
Nous avons :
Un circuit L-C soumis simultanément à des échelons de tension E et de courant J, a pour diagramme de phase Y(X) le cercle de centre G = (E ; J / C.wo) passant par le point
Mo = (Vo ; Io / C.wo). Ce cercle est décrit dans le sens horaire, à partir de Mo, à vitesse angulaire constante wo
5.3 Influence de l'amortissement
Toute inductance réelle comporte une résistance de bobinage r. Prenons en compte cette résistance dans l'étude du circuit de la fig.11. Le facteur de qualité de la bobine est Qo = L.wo / r. Pour t > 0, les équations du circuit sont E = v + L.i'+r.i ; ic= C.dv/dt = i -J. Il vient donc :
E = v +L.C.v"+r.C.v'+r.J soit L.Cv" + r.C.v' + v = E - r.J. Nous avons donc wo = 1 / Ö (L.C) et
z = r/2.L.w o= 1 /(2.Qo). Si nous supposons l'amortissement faible soit z << 1 et Qo >> 1, le régime transitoire est oscillant amorti :
v(t ) = 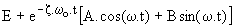 avec w = w o.Ö (1-z²) et
avec w = w o.Ö (1-z²) et
Les conditions initiales donnent vo= E+A et Io = J+C.(w.B- z.A.wo); nous en déduisons : A= V- E et
B = [Io - J +C.z.wo(vo E)]/ C.w.
Si nous supposons z << 1, nous pouvons confondre w et wo.
Nous en déduisons : B = (Io - J)/ C.wo +z.(Vo- E) , C.(w.B- z.A.wo) = Io - J et
C.(w.A+z.wo.B) = z.( (Io - J)+C.wo.(z²+1)( vo E) peu différent de z.( (Io - J)+C.wo.( Vo- E).
Les solutions s'écrivent :
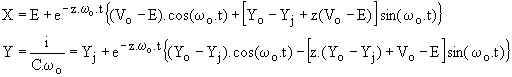
Dans le plan de phase, le graphe Y(X) est une spirale logarithmique (fig.13).
.
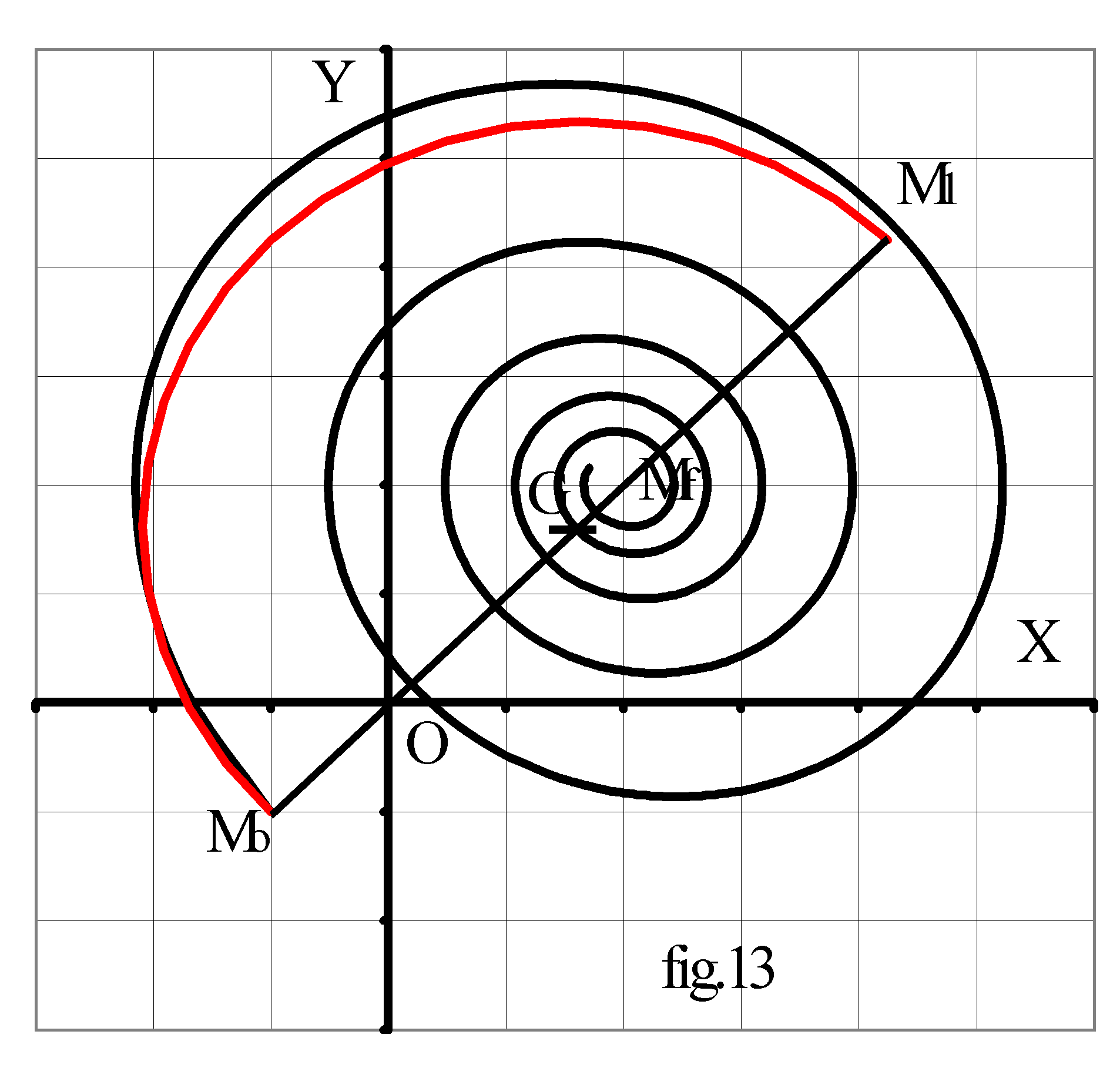
Considérons la première pseudo-période de fonctionnement, soit 0 < t < p/wo; l'amortissement étant faible, sur cet intervalle de temps, la spirale est peu différente du demi-cercle MoM1 ( trait rouge sur la fig.13). Déterminons les coordonnées de M1:
X1 = X(p/wo) =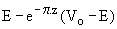 ; Y1 = Y(p/wo) =
; Y1 = Y(p/wo) =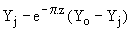 ; en supposant p.z << 1, nous avons
; en supposant p.z << 1, nous avons  ; en posant
; en posant
k = 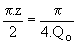 , nous obtenons X1 =2.(1-k).E-(1-2.k).Vo et Y1 =2.(1-k).Yj-(1-2.k).Yo . MoM1 étant le diamètre du cercle, le centre G est au milieu du segment; ses coordonnées sont :
, nous obtenons X1 =2.(1-k).E-(1-2.k).Vo et Y1 =2.(1-k).Yj-(1-2.k).Yo . MoM1 étant le diamètre du cercle, le centre G est au milieu du segment; ses coordonnées sont :
Xg = (X1+Xo)/2 =(1-k).E+k.Vo et Yg = (Y1+Yo)/2 =(1-k).Yj+k.Yo .
Comme dans l'étude à amortissement nul, le diagramme est parcouru dans le sens horaire à vitesse angulaire wo :  .
.
Un circuit R - L - C de faible amortissement tel que p.z << 1, soumis simultanément à des échelons de tension E et de courant J, a pour diagramme de phase Y(X) approché sur l'intervalle de temps 0 < t < p/wo le demi cercle de centre G = [(1-k).E+k.Vo ; (1-k).Yj+k.Yo)] passant par le point Mo = (vo ; Io / C.wo ). Ce demi cercle est décrit dans le sens horaire, à partir de Mo, à vitesse angulaire constante wo .
.
Remarques
v lorsque t ® ¥ , X® E et Y® Yj ; le point Mf de coordonnées ( E ; Yj) est situé sur le diamètre MoM1.
.v Soit r = MoM1/ 2 le rayon du cercle, le vecteura pour coordonnées polaires (r Ð a ), ces coordonnées étant obtenues par une transformation rectangulaire® polaire; Avec
,nous en déduisons les coordonnées polaires de M:
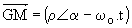
nous en déduisons X-Xg = r.cos(a - wo.t) et Y-Yg = r.sin(a - wo.t); ces équations permettent de calculer v(t) et i(t).
5.4 Exemple
Etudions le circuit de la fig.14 :
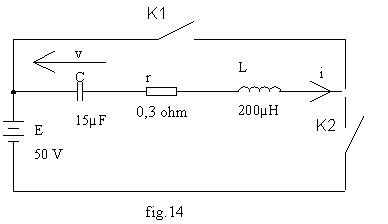
v Pour t < 0, nous supposons que les deux interrupteurs sont ouverts : tous les courants sont nuls et que le condensateur est chargé sous Vo= 100 volts.
v A t = 0, nous fermons K1; le circuit C - r - L mis en court-circuit est alors soumis à l'échelon de tension 0 V et à l'échelon de courant 0 A (pas de source de courant). Nous avons : w o= 1/Ö(L.C) = 18 260 rd/s ; z = r / (2.L. wo) = 0,041 ; Qo = 1 / 2. z = 12,2.
On est donc dans le cas d'un faible amortissement permettant d'utiliser le diagramme de phase simplifié. Le point initial Mo correspond à v = -100 volts et i = 0 soit Mo = (-100 ; 0).
Avec k = = 0,065, le centre G1 du demi-cercle a pour coordonnées :
= 0,065, le centre G1 du demi-cercle a pour coordonnées :
Xg1 = (1-k).0+k.(-100) = -6,45 V et Yg1 = (1-k).0+k.0 = 0.
Nous avons 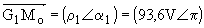 et
et 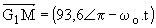 ; nous en déduisons
; nous en déduisons
X = v = -6,45 - 93,6 cos(p - wo.t) =-6,45+93,6 cos(p -wo.t) et Y = i /Cw o= 93,6 sin(p -wo.t) soit i = 25,6 sin(wo.t).
Si nous laissons le montage évoluer sans intervenir, le courant i augmente de 0 à 25,6 A pour t = p /2.wo puis diminue et s'annule pour
t = p /wo ; à cet instant la diode D1 se bloque et le fonctionnement s'arrête au point M1 = (87,1 V ; 0); le montage permet l'inversion de la charge du condensateur C mais la perte d'énergie dans la résistance r fait que l'on retrouve en valeurs absolues une tension inférieure à celle de départ.
.
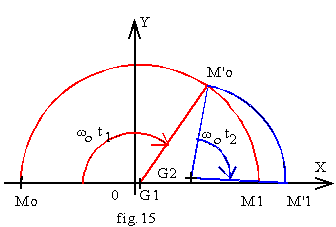
v Sans attendre le blocage de D1, on ferme K2 à l'instant to = 120 µs; posons t' = t - to ; en t' = 0, les grandeurs d'état v et i sont continues et gardent les valeurs correspondant au point M'o de la fig.15. Avec les équations ci-dessus, nous obtenons M'o = (48 V; 76 V). Pour t' > 0, le circuit C - r - L est soumis à l'échelon de tension E et à l'échelon de courant J = 0; son diagramme de phase approché est donc le demi-cercle de centre G2 de coordonnées Xg2 = (1-k).50+k.48 = 49,9 V et
Yg2 = (1-k).0+k.76 = 4,9 V.
Nous avons  nous en déduisons donc : X = v = 49,9 + 71,2 cos(1,6 -wo.t) et
nous en déduisons donc : X = v = 49,9 + 71,2 cos(1,6 -wo.t) et
Y = i /Cwo= 4,9 + 71,2 sin(1,6 -wo.t) soit i = 1,3+19,5 sin(1,6 -wo.t).
Si nous ouvrons K2 en t'2 lorsque i = 0; de l'expression de i, nous tirons la valeur de ce temps :
t'2 =91,4 µs puis nous calculons la valeur de v soit v = 121 V; avec ce circuit dit d'apport d'énergie, nous avons inversé la charge du condensateur tout en obtenant en valeur absolue une tension supérieure à la tension initiale.
Cet exemple nous montre que l'étude des circuits R-L-C de faible amortissement est facilité par la méthode du plan de phase en évitant la résolution d'équations différentielles.

