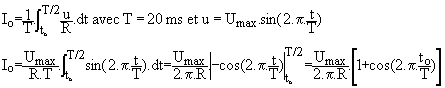|
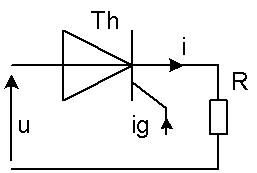
Les caractéristiques du thyristor utilisé sont :
VRRM = VDRM = 400 V ; IFAV = 16 A ; IH = 20 mA
VGT = 3 V ; IGT = 80 mA
Quelle est la valeur maximale de la tension efficace U ? Lorsque le thyristor est bloqué, sous tension directe ou inverse i = 0 donc la d.d.p. aux bornes de Th est v = u.
On doit donc avoir Umax < VRRM = VDRM
soit U / VRRM / Ö2 = 282 V
Quelle est la valeur minimale de Vgmax ? On doit avoir Vg > Vgt pour un amorçage certain soit Vgmax > 3 V
Quelle valeur de Igmax conseillez-vous ? Pour un bon amorçage, on doit avoir Ig de l'ordre de 3.Igt soit 240 mA
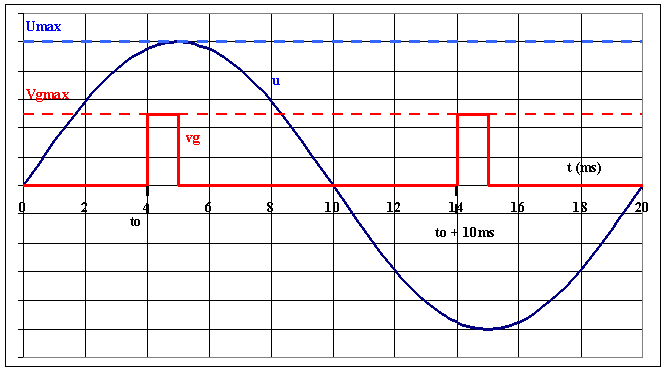
Pour 0 < t < to quel est l'état du thyristor ? Quelle est la valeur de i ? Le thyristor est en polarisation directe avec Ig = 0; il est donc bloqué et i = 0
Pour t > to quel est l'état du thyristor ? Quelle est la valeur de i ? Le thyristor est en polarisation directe avec Ig > 0; il est donc passant et i = u / R
Quel est le mode de blocage de Th et à quel instant se bloque-t-il ? Le blocage est naturel par annulation de i en même temps que u soit en t = 10 ms
Que se passe-t-il en to + 10 ms ? Rien ; le thyristor s'est bloqué en t = 10 ms ; pour t > 10 ms on a i = 0 et v = u < 0
Le courant de gâchette ne peut amorcer un thyristor en polarisation inverse donc Th reste bloqué
Donner l'expression de l'intensité moyenne Io en fonction de Umax, R et to Le thyristor conduit de to à 10 ms ; on a alors i = u/R
Pour U = 130 V, quelle est la valeur minimale de R ? On doit avoir Io < IFAV
Io est maximal pour to = 0 et vaut alors Umax /p.R
R > Umax / p.IFAV = 3,66 W
Pour U = 130 V, quelle est la valeur maximale de R permettant un fonctionnement correct ? Pour que le thyristor reste passant à la fin de l'impulsion de gâchette, il faut que i > Ih ; si Imax = Umax /R < Ih le montage ne fonctionnera jamais correctement
Il faut donc R < Umax / Ih = 2 298 W
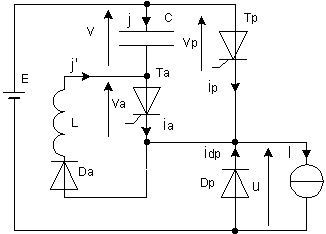
Montrer que Dp conduit Le courant I continu, ne peut passer que dans Dp; cette diode conduit imposant u = 0
Peut-on amorcer Tp ? vp = E - u = E donc Tp, polarisé en direct est amorçable
Si on amorce Tp peut-on le bloquer ultérieurement ? Si on amorce Tp, vp = 0 donc u = E ; Dp polarisée en inverse se bloque donc ip = I = Cste
Tp ne peut se bloquer naturellement puisque ip = Cste > 0
on ne dispose dans le montage d'aucune tension négative à appliquer à Tp pour forcer son blocage.
Tp ne pourra donc être bloqué.
Tp étant bloqué, peut-on amorcer Ta ? va = E - u = E donc Ta, polarisé en direct est amorçable
on suppose Ta amorcé en t = 0. Quels sont les états de Da et Dp ? Ta étant amorcé va = 0 ; u + va + v = E donne u = E donc Dp se bloque
va étant en fait de l'ordre de 1 V, Da est polarisée en inverse donc est bloquée
donner les expressions de j(t), v(t) Ta conduisant seul, on a j = ia = I
j = I = C.dv/dt donc v = I.t / C
montrer que Ta se bloque en t = t1 Tant que Ta conduit, j = I donc v augmente et va = 0
La tension u ne peut devenir négative sans provoquer la mise en conduction de D donc v est limitée à E
Quand v = E, u = 0 donc D conduit et ta va être polarisé en inverse donc se bloquer
v(t1) = E donc t1 = C.E/I
Soit t2 > t1 ;on pose t' = t - t2; en t' = 0 on amorce Tp. Quel est l'état de Dp, Da et Ta ? Après le blocage de Ta , Dp conduit donc u = 0 et vp = E; on peut donc amorcer Tp. L'amorçage de Tp impose
vp = 0 donc u = E; Dp polarisée en inverse se bloque.
va = vp - v = 0 - E < 0, donc ta est bloqué
Si Da est bloquée, j' = 0 donc vda = - va = E > 0; ceci est impossible donc Da conduit
donner les expressions de ip(t'), v(t'), j(t'), j'(t'). Le circuit L - C est mis en court-circuit par Tp et Da
v + L.dj' / dt = 0 ; j' = j = C.dv/dt donc
v +L.C.d²v/dt² = 0; en posant w =1/ÖL.C, il vient
v = A.cos(w.t) + B.sin(w.t)
j = j' = C.dv/dt = C.w.[Bcos(w.t) - A.sin(w.t)]
v(0) = E et j(0) = j'(0) = 0
on en déduit A = E et B = 0
v = E.cos(w.t) ; j = j' = -C.w.E.sin(w.t) ip = I + j
montrer que Da se bloque en t = t3. Da ne peut conduire que si j = j' < 0
j = j' = -C.w.E.sin(w.t) donc da se bloque en t'3 = p / w
A cet instant v = - E
En t = t4> t3, peut-on amorcer Ta ? Tp conduit donc vp = 0 ; va = v- v = E > 0 donc Ta peut être amorcé
on pose t" = t - t4; en t" = 0 on amorce Ta. Quel est alors l'état de Tp, Ta et Dp? Ta étant amorcé va = 0 donc vp = va + v = - E ; Tp se bloque
u+ va +v = E donc u = 2.E ; Dp polarisée en inverse est bloquée
Da court-circuité par ta est bloquée
donner les expressions de v(t"), j(t"). Ta conduisant seul, on a j = IA = I
j = I = C.dv/dt" ; v(t" = 0) = -E donc v(t") = I.t" / C - E
montrer que Ta se bloque en t" = t"5 Tant que Ta conduit, j = I donc v augmente et va = 0
La tension u ne peut devenir négative sans provoquer la mise en conduction de Dp donc v est limitée à E
Quand v = E, u = 0 donc Dp conduit et Ta va être polarisé en inverse donc se bloquer
v(t"5) = E donc t"5 = 2.C.E/I
Quelle est la valeur efficace maximale de la tension u ? Lorsque le triac est bloqué, sous tension directe ou inverse
i = 0 donc la d.d.p. aux bornes est v = u.
On doit donc avoir Umax < VRRM = VDRM
soit U / VRRM / Ö2 = 141 V
Quels sont les instants d'amorçage du triac et quels sont les modes d'amorçage utilisés ? Les instants sont to, to + 10 ms, to+20 ms ...
En to on est en polarisation directe avec Ig > 0 : Mode 1
en to+ 10ms on est en polarisation inverse avec Ig > 0 : Mode 4
quels sont les instants de blocage du triac Le triac se bloque naturellement quand i = 0 soit pour u = 0
les instants de blocage sont to+10 ms, to+20ms ...
Pour U = 48 V quelle est la valeur minimale de R ? Le courant efficace est maximal quand to = 0; on a alors en permanence u = v = R.I
I < IFRMS donc R > U / IFRMS = 8 ohms