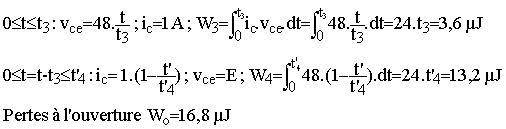|
Pour tous les exercices, on pourra consulter un tableau des caractéristiques de divers transistors en cliquant sur l'icone ci-dessous
Pour un transistor linéaire ou saturé on rendra |Vbe| = 0,7 V et on négligera Ib devant Ic.
Pour un transistor saturé, on prendra |Vce| = 0,1 V
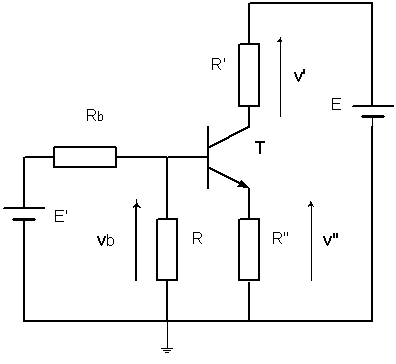
Montrer que l'on peut remplacer l'ensemble E', Rb et R, vu entre base et masse par un seul générateur f.é.m. de Thévenin : base débranchée Eth = k.E'
avec k = R/(R + Rb)
E' en CC on a entre base et base :
Rth = R.Rb / (R+Rb) = k.Rb
Pour Rb = 10 kW quel est l'état du transistor ? k = 0,5 ; Eth = 4,5 V et Rth = 5 kW
Si T est bloqué alors Ib = Ic = 0 ; v' = v" = 0 ; vb = vbe = 4,5 V impossible pour un transistor bloqué
Si T est dans l'état linéaire Vbe = 0,7 V et Ic = Ie = b.Ib avec b = 100
Vb = Vbe + v" = Vbe + R".b.Ib = Eth - Rth.Ib
Ib = (Eth - Vbe)/ (Rth + b.R") = 392 µA
Ic = 39,2 mA ; v' = v" = 1,84 V ; Vce = E - v' - v" = 11,32 V
On a Ib > 0 , Ic > 0 , Vce > Vbe donc l'hypothèse de l'état linéaire est validée
Pour Rb = 10 kW quelle est la puissance dissipée par le transistor ? Le transistor risque-t-il d'être détruit ? P = Vce . Ic = 444 mW
Le transistor ne risque pas d'être détruit car Ic < Icmax, Vce < Vcemax, P < Pmax
Pour Rb = 330 W quel est l'état du transistor ? k = 0,968 ; Eth = 8,7 V et Rth = 319 W
Comme au 2°, l'hypothèse T bloqué ne peut être validée
Si T est dans l'état linéaire Vbe = 0,7 V et Ic = Ie = b.Ib avec b = 100
Vb = Vbe + v" = Vbe + R".b.Ib = Eth - Rth.Ib
Ib = (Eth - Vbe)/ (Rth + b.R") = 1,61 mA
Ic = 161 mA ; v' = v" = 7,58 V ; Vce = E - v' - v" = -0,17 V
On a Ib > 0 , Ic > 0 , Vce <Vbe donc l'hypothèse de l'état linéaire n'est pas validée
T est donc saturé ; Ib = 1,61 mA ; Vce = 0,1 V , V' = V" = (E-0,1)/2 = 7,45 V
Ic = V'/R' = 159 mA < b.Ib
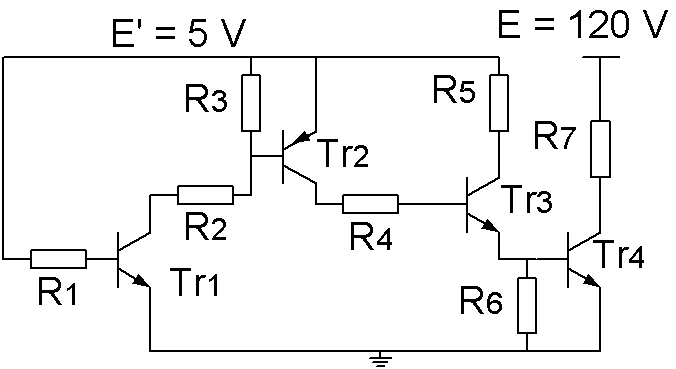
Montrer que Tr1 ne peut être bloqué; calculer son courant de base. Si Tr1 est bloqué, Ib1 = 0 donc aucune chute de tension dans R1 et Vbe1 = 5 V > Vt donc impossible.
Si Tr1 conduit Vbe1 = 0,7 V
Ib1 = (E'-Vbe1)/R1 = 13 µA
Montrer que Tr1 est saturé Si Tr1 est dans l'état linéaire ; Ic1 = b1.Ib1
Le tableau des transistors donne b1 = 100 donc Ic1 = 1,3 mA ; la d.d.p. aux bornes de R2 serait de 6,1 V > E' ce qui est impossible
Tr1 est donc saturé
Montrer que Tr2 ne peut être bloqué Si Tr2 est bloqué, Ib2 = 0
Tr1 étant saturé Vce1 = 0,1 V
Ir3 = Ir2 = Ic1 = (E' - Vce1) / (R2 + R3) = 0,22 mA
Vr3 = -Vbe2 = R3.Ir3 = 3,88 V
On a donc 3,88 V en direct aux bornes de la jonction JBE2; celle-ci ne peut être bloquée donc Tr2 ne peut être bloqué
Calculer l'intensité dans R3 et celle dans R2. Vérifier que Tr1 est saturé Tr2 est passant donc Vbe2 = -0,7 V ; le courant Ir3 orienté vers le bas est Ir3 = -Vbe2 / R3 = 39 µA
Vr2 = E' - Vce1 - Vr3 = 4,2 V et Ir2 = Ic1 = 894 µA
Ic1 / Ib1 = 69 < b1 donc Tr1 est bien saturé
Montrer que Tr3 et Tr4 ne peuvent être bloqués et que Tr2 est saturé Tr2 étant passant, on a Ic2 < 0 donc sortant par l'émetteur de Tr2
Ib3 = -Ic2 > 0 donc Tr3 ne peut être bloqué et Ic3 > 0
Ie3 = Ic3 > 0 donc Ib4 > 0 ; Tr4 ne peut être bloqué
Ir3 = Ir2 + Ib2 donc Ib2 = 855 µA
Si Tr2 est dans l'état linéaire Ic2 = b2.Ib2 = 100 * 855 µA = 85,5 mA
Tr3 étant passant Vbe3 = 0,7 V ; Tr4 étant un Darlington sa tension base - émetteur à l'état passant est Vbe4 = 1,4 V
Vr4 orientée vers la droite est Vr4 = -R4.Ic2 = 12,85 V
Vbe4 + Vbe3 + Vr4 - Vce2 = E' donne Vce2 = 9,93 V
Or pour un transistor PNP Vce est négatif donc l'hypothèse Tr2 linéaire est fausse; comme Tr2 ne peut être bloqué, il est saturé
Calculer le courant collecteur de Tr2 et en déduire que Tr3 est saturé Calculer le courant collecteur de Tr3 et en déduire que Tr4 est saturé Tr2 étant saturé Vce2 = -0,1 V; Vbe4 + Vbe3 + Vr4 - Vce2 = E' donne
Vr4 = 2,28 V soit Ic2 = -Vr4 / R4 = -18,7 mA ; Ib3 = -Ic2 =18,7 mA
Si Tr3 est dans l'état linéaire Ic3 = b3.Ib3 = 40 * 18,7 mA = 747 mA
Vbe4 + Vce3 + R5.Ic3 = E' donne Vce3 = -12,8 V
Or pour un transistor NPN Vce est positif donc l'hypothèse Tr3 linéaire est fausse; comme Tr3 ne peut être bloqué, il est saturé
Cliquez iciTr3étant saturé, on a Vce3 = 0,1 V donc
Vr5 = E' - Vce3 - Vbe4 = 3,5 V ; Ic3 =Vr5 / R5 = 159 mA
Vr6 = Vbe4 = 1,4 V donc Ir6 = 30 mA
Ib4 = Ie3 - Ir6 = Ic3 - Ir6 = 129 mA
Si Tr4 est dans l'état linéaire Ic4 = b4.Ib4 = 120 * 129 mA = 15,5 A
Vce4 + R7.Ic4 = E donne Vce4 = -113 V
Or pour un transistor NPN Vce est positif donc l'hypothèse Tr4 linéaire est fausse; comme Tr4 ne peut être bloqué, il est saturé
Calculer l'intensité dans R7 Tr4 étant saturé, on a Vce4 = 0,1 V
Vr7 = E - Vce4 = 119,9 V ; Ic4 =Vr7 / R7 = 7,99 A
Calculer la puissance dissipée par chaque résistance et chaque transistor Dans les résistances, on dissipe R.I² et dans les transistors Vce.Ic
Choisir le transistor Tr1 Tr1 est de type PNP
Sa tension de blocage doit être supérieure à 24 V
En saturation Ic = E / R1 =5,1 A
On choisit un transistor de type MJE4353 ou un Darlington BDX88C
Pourquoi est-il préférable de choisir un Darlington ? Si on choisit un transistor simple le gain forcé sera de l'ordre de 5, il faudra donc un courant de base de l'ordre de 1 A ; le bloc de commande devra donc amplifier le courant d'un facteur 1 000; il devra comporter 2 à trois étages d'amplification
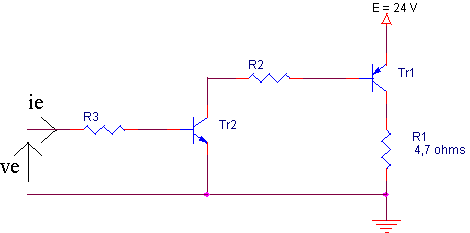
On choisit un taux de saturation de 20 pour Tr1; essayer une synthèse avec un seul étage d'amplification. Que peut-on en déduire ?
Lorsque Ve = - 5 V, Tr1 et Tr2 sont bloqués
Lorsque Ve = + 5 V, Tr1 et Tr2 sont saturés
Ic1 = 5,1 A ; b1 = 750 donc b1sat = 750 /20 = 37,5 ; Ib1 = Ic1 / b1sat = 136 mA
Vce2 + R2.Ib1-Vbe1 = E ; Vce2 = 0,1 V et Vbe1 = -1,4 V
R2 = 22,5 /0,136 = 165 W ; prenons R2 = 150 W ; Ib1 = Ic2 = 150 mA
On peut prendre pour Tr2 un type 2N1711
b2lin = 100 avec un taux de saturation de 3, b2sat = 33 donc
Ib2 = 4,55 mA > Iemax
Il faut rajouter une étage ou pendre un darlington pour Tr2
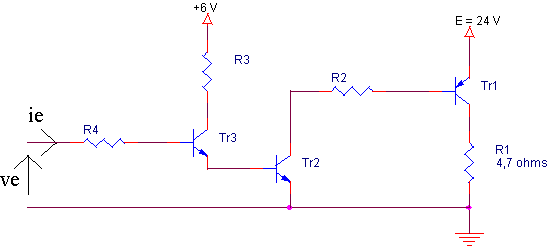
Faire la synthèse du bloc de commande
On garde les composants Tr1, Tr2 et R2 de la question 3
On a donc : Ib2 = 4,55 mA donc Ic3 = Ie3 = 4,55 mA
Tr3 doit pouvoir conduire ce courant en saturation et supporter 6 V au blocage; on peut prendre un type BC107
Vbe2 + Vce3 + R3.Ic3 = 6 V donne R3 = 1,14 kW soit R3 = 1 kW et Ic3 = 5,2 mA
b3lin = 110 avec un taux de saturation de 3, b3sat = 37 donc Ib3 = 0,14 mA <Iemax
Vbe2 + Vbe3 + R4.Ib3 = 5 V donne R4 = 25,5 kW soit R4 = 22 kW
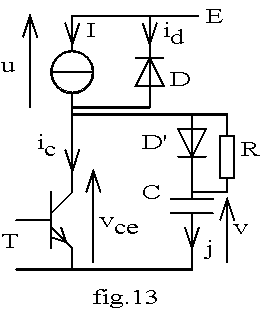
Le circuit R,C, D' étant débranché, on a relevé les graphes suivants Quelles sont les valeurs de E et I ? E = 48 V et I = 1 A
Quels sont les temps de fermeture et d'ouverture ? Temps de fermeture = temps entre l'instant depassage de la commande au niveau haut et l'instant de passage de ic à 90 % de Icsat
ton = 575 ns
Temps d'ouverture = temps entre l'instant depassage de la commande au niveau bas et l'instant de passage de ic à 10 % de Icsat
toff = 580 ns
Estimer l'énergie perdue à la fermeture, celle perdue à l'ouverture et les pertes totales de commutation A la fermeture ic monte en t1 = 650 ns avec vce = E puis de t1 à t2 = 700 ns, vce s'annule à ic = Cste = 1 A :
A l'ouverture vce monte en t3 = 150 ns avec ic = 1 Apuis de t3 à t4 = 550 ns, ic s'annule à vce = Cste = 48 V:
L'énergie totale perdue est donc de 49,2 µJ . La période étant de 2 µs, on a une puissance W /T = 24,6 W
Calcul du circuit d'aide à l'ouverture pour une fréquence de commande de 25 kHz Calculer la capacité du condensateur C Les deux conditions sont :
C >> I.tf/2.E et C < (tblocmin - toff).I /E
I = 1 A ; E = 48 V ; tf = temps de descente de ic = 500 ns ; tblocmin = T/2 = 20 µs
C >> 5,2 nF et C < 405 nF on peut prendre C = 68 nF
Calcul la résistance R Les deux conditions sont :
R > E / (ICM - I) et R < (tcondmin - ton) /3C
ICM = 5 A, tcondmin = T/2 = 20 µs
R > 12 W et R < 65 W on peut prendre R = 33 W