Il existe de nombreux outils de mesure des écarts de revenus.

- On peut d’abord faire référence à une position centrale comme le revenu moyen ou le revenu médian.

Le revenu moyen est obtenu en rapportant le total des revenus disponibles de tous les ménages (corrigés par équivalence) au nombre de ménages. Le revenu médian est celui qui partage la distribution des revenus des ménages en deux parts égales : 50 % des ménages sont en dessous du revenu médian et 50 % au dessus.

- Par analogie avec cette notion de médiane, il est logique de regrouper les ménages par « tranches » ou catégories d’effectifs égaux, séparés par des quantiles. Quand la « tranche » regroupe 10 % des ménages on parle de déciles et il y a 9 déciles puiqu’il faut 9 valeurs pour partager la distribution en 10 parts égales, de quintiles (au nombre de 4) quand l’effectif représente 20 % et de quartiles (au nombre de 3) pour 25 %. Le nombre des quantiles peut être étendu, ainsi on utilise parfois une décomposition en centiles (il y en a 99).

Les représentations graphiques des inégalités de revenus sont nombreuses.

- Un histogramme avec en abscisses les tranches de revenus et en ordonnées les effectifs dans chaque tranche. Il est toujours caractérisé par une nette dissymétrie en faveur des hauts revenus. On passe à la distribution des revenus en termes de fréquence, en portant en ordonnée le pourcentage de la population ayant un revenu donné et en abscisse le revenu.

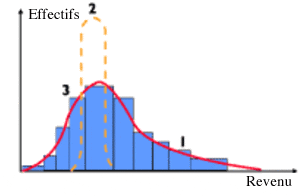
Un second procédé, consiste à porter en ordonnées les revenus et en abscisses les individus classés selon le revenu. Le choix d’une représentation pour décrire une distribution n’est pas neutre et il commande souvent l’interprétation. Si l’on souhaite mettre en valeur les inégalités, on préférera la figure de Pen qui souligne l’écart entre les revenus de quelques personnes exceptionnellement riches et la plupart des autres.

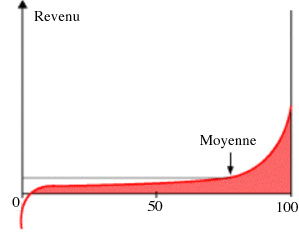
- Une autre représentation est très souvent utlisée. Elle consiste à porter en ordonnées les effectifs cumulés, en pourcentage, du plus pauvre au plus riche, mais à porter en abscisses non pas le revenu, mais les pourcentages cumulés du revenu total On voit sur cette figure que les 50 % les plus pauvres reçoivent 13 % du revenu total. De même, les 10 % les plus riches perçoivent 50 % du revenu total. Cette courbe est appelée courbe de Lorenz. Si tous les individus avaient le même revenu, cette courbe se confondrait avec la diagonale ; à l’opposé si un seul recevait tout et les autres rien, la courbe suivrait les deux axes.

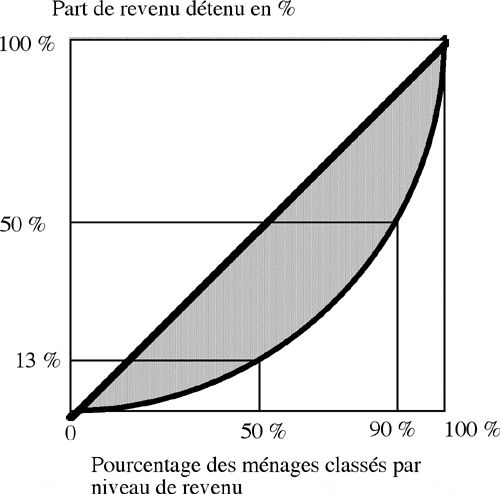
Plus la courbe est éloignée de la diagonale et plus l’inégalité est importante.

- En rangeant les ménages par groupe de 10%, en commençant par les 10% percevant les plus faibles revenus (par extension on dit parfois le « premier décile » pour qualifier l’ensemble des ménages situés en dessous du premier décile) et en allant jusqu’aux ménages percevant les plus hauts revenus ("dixième" décile) on dispose d’une représentation se prétant à de nombreux calculs.

La part de chaque décile indique quelle proportion du revenu moyen par ménage reçoivent les ménages classés dans ce décile. Par exemple, si les parts respectives du premier et du dixième déciles, sont 2 % et 30 %, on sait que le revenu moyen des ménages classés dans le premier décile représente 20 % du revenu moyen et celui des membres du dixième décile 3 fois le revenu moyen.

On en déduit le rapport des revenus moyens entre les deux déciles 0,2 / 3 soit un rapport de 1 à 15. Au lieu de considérer le revenu moyen de chaque décile, on peut se référer à la valeur de chaque décile (limite supérieure de la tranche). D1 représente la valeur du revenu au-dessous duquel se classent 10 % des actifs, D9 la valeur correspondante pour 90 % des actifs. Le rapport entre D1 et D9 est toujours inférieur à celui qui s’établit entre les revenus moyens des "déciles" 1 et 10.

On appelle rapport interdécile ce résultat D9 / D1 et écart interdécile la différence D9 - D1.

Cette méthode est applicable même quand l’information sur les hauts ou les bas revenus n’est pas fiable ce qui est souvent le cas. Même s’il est impossible d’établir un histogramme pour ces tranches de revenus, ou une courbe de Lorenz pour l’ensemble de la population on peut calculer l’écart ou le rapport entre D1 et D9. Cependant, deux pays ayant des écarts ou rapports interdéciles identiques, ne sont pas forcément caractérisées par une même inégalité, il suffit en effet pour qu’il en aille autrement que le revenu moyen du dernier vingtième soit le double dans un des deux pays de ce qu’il est dans l’autre.

- Lorsqu’on dispose d’une représentation graphique de la courbe de Lorenz on peut facilement claculer le coefficient de Gini en faisant le rapport de l’aire de la surface comprise entre la courbe de Lorenz et la première bissectrice, notée « zone Lorenz » sur le graphique ci-desoous, et celle du triangle ABC, et comme celle-ci vaut 0,5 cela revient à prendre deux fois la valeur de l’aire « zone Lorenz ».

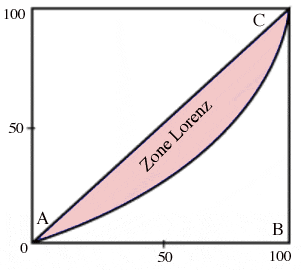
- L’inconvénient du coefficient de Gini est que des courbes de Lorenz très différentes peuvent correspondre à la même valeur de du coefficient G. Ainsi sur la figure ci-dessous les deux courbes se croisent, et la courbe 1 reflète une distribution plus défavorable pour les deux premiers quintiles, la courbe 2 une distribution plus favorable pour le cinqième quintile. Que ces courbes correspondent à la même valeur de G, ou à des valeurs différentes, il est impossible d’affirmer qu’une distribution est plus inégale que l’autre dès lors que les courbes se croisent. On en a la preuve si l’on calcule l’inégalité pour chaque distribution avec divers indicateurs. Selon que ceux-ci sont plus sensibles aux bas ou aux hauts revenus, ils classeront la distribution 1 avant ou après la distribution 2.

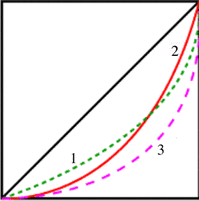
Pour pouvoir affirmer qu’une distribution 1 est plus inégale que la distribution 2, quel que soit l’indicateur choisi, il faut qu’il y ait dominance, c’est-à-dire que la courbe 1 englobe en totalité la courbe 2 (ce qui est le cas de la courbe 3 dans la figure ci-dessus). Dans ces conditions, dans tous les cas où il n’y a pas dominance, il faut compléter le coefficient de Gini par le recours à d’autres indicateurs d’inégalité afin de donner une information plus complète et objective. Dans ce but on utilise souvent les indicateurs de Theil ou d’Atkinson.