Pour mesurer la productivité d'un facteure de production, il faut le faire e posant que la quantité de l'autre facteur ne change pas, car la production dépend des deux facteurs. UN même travailleur doté de deux outils différents n'a pas la même productivité mais cela ne vient pas de lui, cela vient en fait de l'outillage.
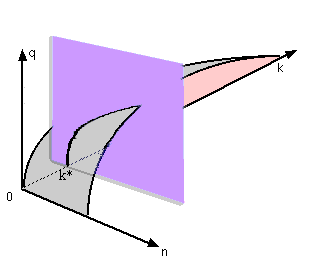
Graphiquement une fonction de production à facteurs substituables se présente, en 3 dimensions

Si on veut étudier le rôle d'un facteur l'autre étant fixé à une quantité donnée, il faut réduire la représentation dans 2 dimensions en coupant le graphique de droite par un plan parallèlle au plan vertical 0nq à niveau donné de capital par exemple k*. On obtient une trace qui est une fonction à une seule variable s'écrivant : q= f (n,k*) La représentation de cette fonction, en faisant les hypothèses habituelles, fonction continue, croissante mais avec une productivité marginale du travail décroissante permet de relier la production et les productivités.
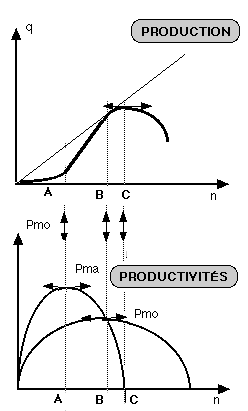
	Jusqu'au point A la production augmente de plus en plus vite, chaque unité de travail supplémentaire est plus efficace que les précédentes, donc supérieure à la productivité moyenne. Après A et jusqu'en B ajouter du travail permet d'augmenter la production mais de moins en moins vite, la productivité marginale diminue. Tant qu'elle est supérieure à la productivité moyenne, celle-ci continue d'augmenter. Après le point B la productivité marginale devient inférieure à la productivité moyenne, chaque unité de travail supplémentaire est moins efficace que la moyenne, cela entraîne la baisse de la productivité moyenne. La productivité moyenne du travail est maximum pour la quantité de travail qui égalise la productivité moyenne et la productivité marginale.

Mathématiquement la productivité moyenne pmo est égale à q / n
la productivité marginale est Δq / Δn ou le signe Δ indique une variation, si on fait tendre Δn vers 0 la productivité marginale est la dérivée de la fonction q = f(n,k*) par rapport à n soit pma = dq / dn.

Pour que la productivité moyenne soit maximum il faut que sa dérivée s'annule soit : d(pmo) / dn = 0

donc [(dq /dn) n - q] / n² = 0 ou encore (dq /dn) n = q soit le résultat recherché : dq / dn = q / n (la productivité moyenne du travail est maximum pour la quantité de travail qui égalise la productivité moyenne et la productivité marginale.)