
|
Croissance du PIB et évolution annuelle du taux de chômage en France
|
|
|
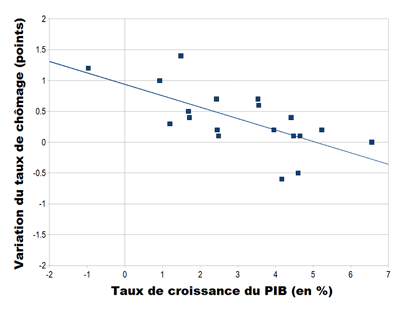
entre 1970 et 1989
|
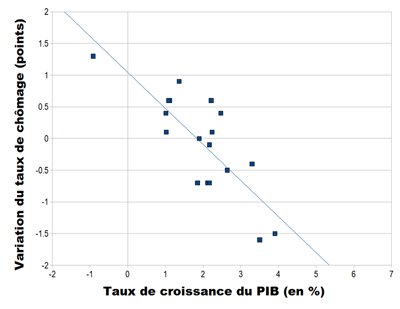
entre 1990 et 2007
|
 |
 |

|
Croissance du PIB et évolution annuelle du taux de chômage en France
|
|
|
entre 1970 et 1989
|
entre 1990 et 2007
|
 |
 |
Si on appelle Ut le taux de chômage de l'année t et Gt le taux de croissance du PIB pour l'année t, la relation s'écrit Ut - Ut-1 = a (Gt - b).
Pour la première période la régression linéiare donne la relation Ut - Ut-1 = - 0,19 (Gt - 4,94%) = - 0,19 Gt + 0,93% ce qui revient à dire que pour que le chômage n'augmente pas le PIB doit augmenter d'au moins 5 %. Le chômage est pendant cette période peu sensible à la croissance de la production (pour réduire le taux de chômage d'un point il faut une croissance très rapide - de l'ordre de 10%).
Pour la seconde période la relation devient Ut - Ut-1 = - 0,57 (Gt - 1,84%) = - 0,57 Gt + 1,04%. Pour que le chômage n'augmente pas il faut 2% de croissance annuelle et pour réduire le chôamge d'un point il faut une croissance du PIB de l'ordre de 3,8%.
Les économistes disent que la croissance est devenue plus riche en emplois. Cet enrichissement a deux raisons principales : d'une part la productivité du travail augmente beaucoup moins vite dans la deuxième période (près de deux fois moins vite) et d'autre part, les transformations du marché du travail ont rendu celui-ci plus flexible. Les entreprsies ajustent plus rapidement l'emploi lorsque le rythme de croissance varie.
Le terme b dans l'expression générale est le taux de croissance de la production en dessous duquel le taux de chômage augmente. Le niveau de ce taux minimal de croissance est donc celui qui compense les augmentations de la population active et de la productivité du travail. Si la population active augmente de 0,5 % et la productivité du travail de 2%, le chômage augmentera si la production n'augmente pas d'au moins 2,5%.