La courbe de demande agrégée ou demande globale

Analytiquement Il faut reprendre le modèle IS-LM en intégrant le niveau des prix. La demande de monnaie contient une demande de monnaie de transaction (fonction du revenu Y) et une demande de monnaie de spéculation (fonction du taux d'intérêt r). La demande de monnaie de transaction augmente quand le revenu augmente, la demande de monnaie de spéculation diminue quand le taux d'intérêt augmente (il vaut mieux alors faire des placements, acheter des titres). Quand les prix peuvent varier, les agents raisonnent en pouvoir d'achat et demande des "encaisses réelles" (la quantité de monnaie qu'ils détiennent dépend des prix). La demande d'encaisses réelles s'écrit : M^d / P = L(Y , r) où M^dest la quantité de monnaie demandée et L(Y , r) une fonction associant une valeur de M^d / P à chaque couple de valeurs de Y et de r. Pour simplifier on peut considérer que la demande de monnaie pour les transactions et celle pour la spéculation sont proportionnelles respectivement au revenu Y et au taux d'intérêt r (avec λ_Tet λ_S des coefficients positifs) L(Y , r) = λ_TY - λ_S r -------- ce qui permet d'écrire -------r = (1 / λ_S) [λ_T Y - (M / P)]. Pour le marché des biens on retient laprésentation habituelle : la consommation C dépend du revenu diminué des prélèvements obligatoires, Y - T , avec une propension à consommer le revenu disponible égale à c (compris entre 0 et 1) et une consommation incompressible C₀; l'investissement I est fonction du taux d'intérêt r ; les dépenses publiques étant supposées autonomes. En adoptant une version linéiare simple des fonctions de consommation et d'investissement (a est un coefficient positif et I₀ est un investissement autonome indépendant du taux d'intérêt par exemple pour les invsetissements de remplacement) C = cY -c T + C₀----- et ---- I = I₀ - a r ----cce qui donne Y = cY -c T + C₀ + I₀ - a r + G ---c ou encore Y = [1 / (1 - c)] (A - a r) ---cou A est la dépense autonome (C₀ - c T + I₀+ G) En utilisant la relation donnant le taux d'intérêt on trouve Y = k [ A + ( a / λ_S ) ( M / P) --------aavec ----k-= 1 / [ 1 - c + a ( λ_T / λ_S ) ]----atous les coefficients sont positifs ----------------------------------------------------------A = (C₀ - c T + I₀+ G) On voit que toutes choses égales par ailleurs une augmentation de P réduit le niveau de la production. Le niveau de production est une fonction décroissante du niveau des prix.
Graphiquement
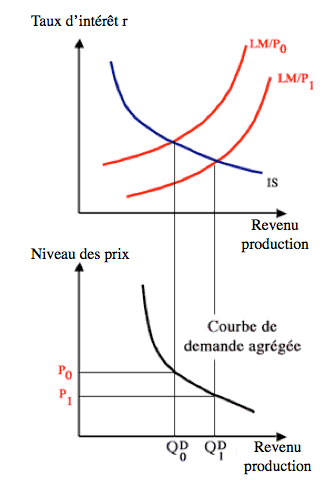
Une augmentation du niveau des prix entraîne un déplacement de la courbe LM vers la gauche. Pour un même niveau de production ou de revenu le taux d'intérêt s'élève sous l'effet de la hausse des prix.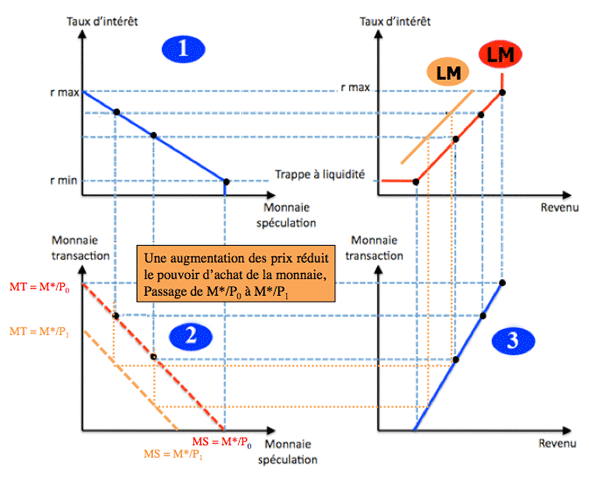	En transposant ce déplacement dans le modèle IS-LM on peut tracer la courbe de demande globale.